Journal influence
Bookmark
Next issue
Absolute stability of explicit difference schemes for the heat equation under Fourier–Tikhonov regularization
Abstract:The paper considers the possibility of constructing a simple and absolutely stable explicit difference scheme for the heat equation. Due to the too rigid stability condition, the invention of the sweep method for solving SLAE with three diagonal matrices, and splitting schemes, absolutely stable implicit schemes forced out explicit schemes for the heat equation of programming practice. However, implicit schemes are poorly parallelized. Therefore, programs for solving problems of heat conduction, diffusion, underground hydrodynamics, etc. on huge spatial grids using multiprocessor computing systems require using explicit difference schemes. This is especially true for multiprocessor systems of teraflop and higher performance that combine hundreds of processors. In this case, explicit schemes must be absolutely stable or, in the extreme case, their stability condition must be no more stringent than the same for hyperbolic equations. The paper proposes modifications of explicit difference schemes that approximate a parabolic equation and have absolute countable stability. Countable stability of a solution obtained at each time step by the classical explicit scheme is achieved by the fast Fourier transform and the subsequent Fourier synthesis with Tikhonov regularization. When calculating the direct and inverse Fourier transforms, the author used the Cooley–Tukey algorithm of the fast Fourier transform. There are the results of comparing numerical calculations of model problems with analytical solutions. The absolute stability of the proposed explicit schemes for the heat equation allows their wide use for parallel computations.
Аннотация:В статье рассматривается возможность построения простой и абсолютно устойчивой явной разностной схемы для уравнения теплопроводности. Явные схемы для уравнения теплопроводности были фактически вытеснены из практики программирования абсолютно устойчивыми неявными схемами. Однако неявные схемы плохо распараллеливаются, поэтому программы для решения задач теплопроводности, диффузии, подземной гидродинамики и т.п. на громадных пространственных сетках с использованием многопроцессорных вычислительных систем требуют использования явных разностных схем. Это особенно справедливо для многопроцессорных систем терафлопной и выше производительности, объединяющих сотни процессоров. При этом явные схемы должны быть абсолютно устойчивыми или, по крайней мере, их условие устойчивости должно быть не жестче такого же для гиперболических уравнений. В работе предложены модификации явных разностных схем, аппроксимирующих параболическое уравнение и обладающих свойством абсолютной счетной устойчивости. Счетная устойчивость решения, получаемого на каждом временном шаге классической явной схемой, достигается быстрым преобразованием Фурье и последующим синтезом Фурье с регуляризацией по А.Н. Тихонову. При вычислении прямого и обратного преобразований Фурье использован алгоритм Кули–Тьюки быстрого преобразования Фурье. Приведены результаты сопоставления численных расчетов модельных задач с аналитическими решениями. Абсолютная устойчивость предлагаемых явных схем для уравнения теплопроводности позволяет широко использовать их для параллельных вычислений.
| Authors: Bakhmutsky, M.L. (mbakhmut@mail.ru; ) - Federal State Institution (Associate Professor), Moscow, Russia, Ph.D | |
| Keywords: Fourier transform, regularization, heat conduction equation, explicit schemes |
|
| Page views: 1364 |
PDF version article |
При моделировании пластовых систем приходится решать параболические уравнения, используя громадные пространственные сетки, и рассматривать процессы, протекающие длительное время. Решение таких задач требует применения параллельных вычислений. Однако абсолютно устойчивые неявные схемы плохо распараллеливаются. В то же время условия устойчивости для явных схем налагают слишком жесткие ограничения на временной шаг интегрирования. Известные абсолютно устойчивые схемы фактически аппроксимируют только гиперболическое уравнение, а параболическое уравнение аппроксимируют при t/h ® 0, то есть при выполнении почти столь же жесткого условия, как и для классической явной схемы В.К. Саульева и Дюффорта–Франкела [1, 2]. Существуют абсолютно устойчивые схемы со счетом по явным формулам, называемые «классики» [3, 4]. В работе [3] доказывается сходимость метода с первым порядком в предположении t/h2 = const. Таким образом, абсолютно устойчивые схемы Саульева, Дюффорта–Франкела и «классики» аппроксимируют уравнение теплопроводности и сходятся при выполнении почти столь же жестких условий, как и для классической явной схемы [5–7]. Обобщить закон Фурье, добавив производную потока по времени, умноженную на малый параметр, предлагается в [8]. При этом уравнение теплопроводности становится сингулярно возмущенным гиперболическим уравнением, а условие устойчивости явной схемы для него менее жестким. В работе [9] приведены оценки разности решений задач для параболического и гиперболического уравнений с малым параметром. В [10] предложен алгоритм повышения устойчивости явных схем путем адаптивного сглаживания при помощи спектрально-сингулярного анализа. Однако в данном случае на каждом временном шаге необходимо находить сингулярное разложение траекторной матрицы решения, что может существенно замедлять вычисления. Поэтому при создании программ для многопроцессорных (многоядерных) систем желательно иметь явные схемы, аппроксимирующие уравнение теплопроводности и обладающие абсолютной устойчивостью. Счет по таким схемам не должен быть существенно медленнее счета по простым неявным схемам. В данной работе для достижения безусловной устойчивости счета предлагается использовать регуляризацию решения, полученного на каждом временном шаге по классической явной разностной схеме, при помощи алгоритма Кули–Тьюки быстрого преобразования Фурье [11, 12]. При этом трудоемкость предлагаемых алгоритмов благодаря алгоритму Кули–Тьюки примерно равна трудоемкости метода прогонки. Описание метода. Задача Дирихле Рассмотрим начально-краевую задачу для простейшего уравнения теплопроводности:
u(x, 0) = f(x). (1) Ее аналитическое решение:
где Введем равномерную пространственную сетку Аппроксируем уравнение (1) на этой сетке в виде
u0 = uN = 0, ui(0) = f(xi), и запишем решение этой задачи:
xi = ih, i Î 0 ¸ N,
Пусть
где Рассмотрим с этой точки зрения две классические разностные схемы для задачи (1) первого порядка аппроксимации по t и h: условно устойчивую явную схему
и абсолютно устойчивую неявную схему
а также абсолютно устойчивую схему Кранка–Николсон (схему с весами) второго порядка аппроксимации по t и h:
В момент времени t = nt полагаем
Тогда
Из формулы (5) следует условие устойчивости явной схемы Построим три явные схемы, отличающиеся алгоритмами регуляризации. Предварительно введем обозначения для дискретных прямого и обратного регуляризованного преобразований Фурье:
Схема 1. Введем параметр Поскольку
Квадратные скобки в формуле (10) означают целую часть числа. Для подавления высших гармоник на каждом временном шаге сначала вычисляем промежуточные значения:
Затем находим дискретное преобразование Фурье:
вычисляем решение на n+1-м временном шаге: Строго говоря, предложенный алгоритм не делает явную схему абсолютно устойчивой, а только значительно ослабляет условие устойчивости. Схема 2. На каждом временном шаге строим дискретное преобразование Фурье разностной аппроксимации второй производной:
вычисляем регуляризованную вторую производную
Данный алгоритм является явным, эквивалентным неявной схеме и абсолютно устойчивым. Действительно, если положить
то при непосредственной подстановке (12) в (11) легко убедиться, что результатом алгоритма является соотношение (6). Схема 3. На каждом временном слое сначала находим промежуточное решение:
Нетрудно убедиться в том, что при Алгоритм явной схемы является явным, абсолютно устойчивым и, хотя промежуточное решение не аппроксимирует исходное уравнение, эквивалентным схеме Кранка–Николсон. Пример расчета. Задача Дирихле. Рассмотрим модельный пример задачи Дирихле:
u(x, 0) = 0, u(0, t) = u(l, t) = 0. Задача имеет аналитическое решение:
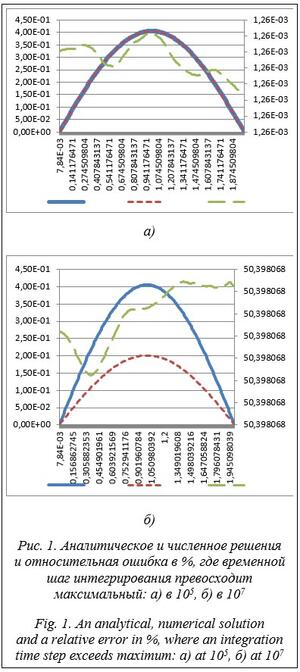
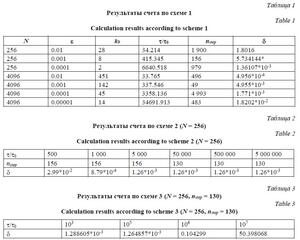
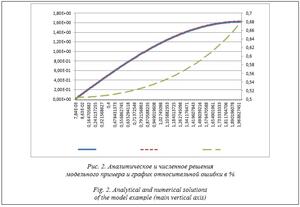
В данном случае аналитическое и численное решения практически совпадают. На рисунке 1б приведены графики аналитического и численного решений (основная вертикальная ось) и график относительной ошибки в % (вспомогательная ось). Для счета использована схема 3, временной шаг интегрирования в 107 раз превосходит максимальный шаг, вытекающий из классического условия устойчивости явной схемы. В этом примере число пространственных узлов N = 256, временных шагов 130. Графики аналитического и численного решений резко отличаются, относительная ошибка везде составляет порядка 50 %.
здесь u(xi, T) – аналитическое, а Приведенные в таблицах примеры демонстрируют абсолютную устойчивость явных разностных схем 2 и 3 и значительное ослабление условия устойчивости для схемы 1. Модификация метода для задачи Неймана. Рассмотрим решение краевой задачи с однородными условиями Неймана на границах х = 0 и х = 1. В этом случае можно использовать построенные выше схемы, в которых достаточно заменить синус-преобразование Фурье на косинус-преобразование Фурье с теми же регуляризирующими множителями. Несколько более сложная ситуация возникает, если на одном конце, например, при х = 0, задано условие Дирихле, а при x = l – условие Неймана. Вместо задачи (1) рассмотрим задачу Ее аналитическое решение:
Схемы 1–3 можно применить, если использовать дискретное преобразование Фурье по функциям
Для нахождения решения на каждом n+1-м временном слое сначала вычисляем промежуточное решение на сетке из 2N узлов:
Далее при помощи алгоритма быстрого преобразования Фурье находим дискретное преобразование Фурье
Схемы 2 и 3 модифицируются аналогичным образом. Пример расчета. Рассмотрим модельный пример:
Эта задача имеет аналитическое решение:
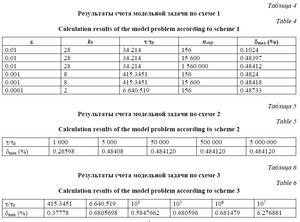
Некоторые результаты счета этой задачи по схеме 1 приведены в таблице 4, по схеме 2 – в таблице 5, по схеме 3 – в таблице 6. Число пространственных узлов N = 256, временных шагов 156. Упрощение регуляризации. Данные, приведенные в таблицах 1–6, свидетельствуют об устойчивости счета по схемам 1–3. Заменой пространственных переменных реальная задача может быть сведена к приведенным схемам. Для многих квазилинейных уравнений эти замены необходимо делать на каждом вре-менном шаге и при этом пересчитывать регуляризирующие множители. Для упрощения процедуры пересчета воспользуемся тем, что Таким образом, используем регуляризирующий множитель Тихонова с параметром регуляризации Пример расчета приведен в таблицах (http://www.swsys.ru/uploaded/image/2023-2/2023-2-dop/12.jpg), где сравниваются численное и аналитическое решения при использовании последних регуляризирующих множителей. Заключение Результаты счета свидетельствуют об абсолютной устойчивости модифицированных алгоритмов явной разностной схемы. Расхождение между численным и аналитическим решениями крайне незначительное даже при большом числе временных шагов и существенном превышении порогового (по условиям устойчивости классической явной схемы) значения временного шага интегрирования. Необходимость прямого и регуляризованного обратного быстрого преобразования Фурье на каждом временном шаге делает использование предлагаемых схем примерно настолько же эффективным, как и простых неявных схем в последовательных программах. Однако абсолютная устойчивость этих явных схем для уравнения теплопроводности позволяет широко применять их для параллельных вычислений. Список литературы
Reference List 1. Saulev, V.K. (1960) Integration of Equations of Parabolic Type by the Method of Grids, Moscow, 320 p. (in Russ.). 2. Roach, P. (1980) Computational Fluid Dynamics, Moscow, 616 p. (in Russ.). 3. Gourlay, A.R. (1970) ‘Hopscotch: A fast second order partial differential equation solver’, IMA J. of Applied Math., 6(4), pp. 375–390. 4. Gourlay, A.R., McGuire, G.R. (1971) ‘General hopscotch algorithm for the numerical solution of partial differential equation’, IMA J. of Applied Math., 7(2), pp. 216–227. 5. Stepanov, M.M., Savelev, S.K. (2019) Numerical Methods for Rocket Building, St. Petersburg, 211 p. (in Russ.). 6. Mazo, A.B. (2018) Computational Fluid Dynamics. P. 1. Mathematical Models, Grids and Grid Schemes, Kazan, 166 p. (in Russ.). 7. Aristova, E.N., Lobanov, A.I. (2015) Practical Classes on Computational Math. in MPTI. P. 2, Moscow, 310 p. (in Russ.). 8. Glotov, V.Yu., Goloviznin, V.M., Chetverushkin, B.N. (2020) ‘Balance and characteristic finite difference schemes for equations of the parabolic type’, Math. Models Comput. Simul., 12(6), pp. 981–989. doi: 10.1134/S2070048220060095. 9. Repin, S.I., Chetverushkin, B.N. (2013) ‘Estimating the difference between approximate solutions of a problem for a parabolic equation and a hyperbolic equation with a small parameter’, Dokl. Math., 451(3), pp. 255–258. doi: 10.7868/S0869565213210056 (in Russ.). 10. Bakhmutsky, M.L. (2015) ‘Integration nonlinear parabolic equation by explicit finite-difference scheme with adaptive smoothing’, Bull. of Cybernetics, (4), p.72–82 (in Russ.). 11. Cooley, J.W., Tukey, J.W. (1965) ‘An algorithm for the machine calculation of complex Fourier series’, Math. of Computation, 19(2), pp. 297–301. 12. Press, W.H., Teukolsky, S.A., Vetterling, W.T., Flannery, B.P. (2007) Numerical Recipes. The Art of Scientific Computing, NY: Cambridge University Press, 1256 p. 13. Lyusternik, L.A. (1956) ‘On difference approximations of the Laplace operator’, Russian Math. Surveys, 9(2), pp. 3–55 (in Russ.). 14. Tikhonov, A.N. (1964) ‘On stable summability methods for Fourier series’, Dokl. Akad. Nauk SSSR, 156(2), pp. 268–271 (in Russ.). 15. Maslakov, M.L., Egorov, V.V. (2022) ‘Regularization of Fourier series with approximate coefficients for the problem of phase probability density function estimation’, SJNM, 25(2), pp. 157–171. doi: 10.15372/SJNM20220205. |
| Permanent link: http://swsys.ru/index.php?page=article&id=5001&lang=en |
Print version |
| The article was published in issue no. № 2, 2023 [ pp. 272-280 ] |
Perhaps, you might be interested in the following articles of similar topics:
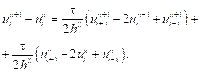 (4)
(4)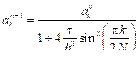 , (6)
, (6)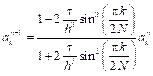 . (7)
. (7)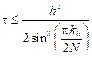 , где k0 определяется из неравенства
, где k0 определяется из неравенства 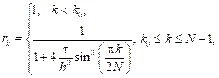
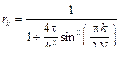 и в итоге находим решение на n+1-м временном слое:
и в итоге находим решение на n+1-м временном слое: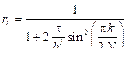 .
.
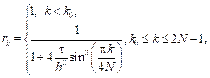 вычисляем
вычисляем 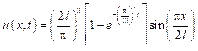 .
.
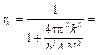
 .
.