Journal influence
Higher Attestation Commission (VAK) - К1 quartile
Russian Science Citation Index (RSCI)
Bookmark
Next issue
№2
Publication date:
16 June 2024
Algorithms of regular time series continuous wavelet transformation: development and software implementation
Date of submission article: 16.10.2017
UDC: 004.94
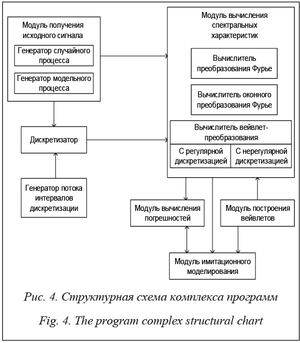
The article was published in issue no. № 4, 2017 [ pp. 765-769 ]Abstract:One of the actively developing directions of data analysis is wavelet transformation. It is used for analyzing medical data, image processing and other purposes. This paper considers methods of calculating coefficients of continuous wavelet transformation of even time series. In the classical approach, calculation of some coefficients is redundant because the value of some wavelets is zero. To remove redundancy, the authors propose using wavelet characteristics in the time domain, which allows obtaining a wavelet window width, wich depends on the given scale. The paper gives the obtained characteristics values of mother wavelets, such as Gaussian wavelets of the 1st to the 8th order, the DOG wavelet and the Morlet wavelet. The proposed algorithm for calculating wavelet values is based on these characteristics. The algorithm allows reducing the number of readings of the used wavelet. For each given scale, there is a determined number of nonzero wavelet values and their calculated values. As a result, we get an array of all wavelet values, which are necessary for transformation. The paper proposes an algorithm for evaluating the coefficients of continuous wavelet transformation. It is based on decreasing repeated calculations of wavelets. The reduction of computations is due to taking into account wavelet invariance regarding a shift. Thus, if we calculate all nonzero wavelet values for all scale once and store it, then it is enough we to refer to the wavelet value by number in array corresponding to the shift. The developed algorithms are implemented as a software package. The paper shows that the proposed algorithm works faster than the classical one without significant loss of calculation accuracy.
Аннотация:Одним из активно развивающихся направлений анализа данных является вейвлет-преобразование, которое применяется для анализа медицинских данных, обработки изображений и в других областях. В статье рассматриваются способы вычисления коэффициентов непрерывного вейвлет-преобразования случайных процессов с регулярной дискретизацией. При классическом подходе вычисление некоторых коэффициентов может оказаться избыточным из-за того, что ряд значений вейвлетов равны нулю. Для устранения избыточности предлагается использовать характеристики вейвлетов во временной области, что позволяет получить ширину окна вейвлета, зависящую от заданного масштаба. Таблица с полученными значениями характеристик для основных вейвлетов, таких как Гаусса 1–8-го порядков, DOG-вейвлета и вейвлета Морле, приведена в статье. На их основе предложен алгоритм вычисления значений вейвлетов, который позволяет уменьшить число отсчетов используемого вейвлета: для каждого заданного масштаба определяется число ненулевых значений вейвлета и вычисляются их значения. Таким образом, в результате получаем массив всех значений вейвлетов, необходимых для преобразования. Для оценки коэффициентов непрерывного вейвлет-преобразования предложен алгоритм, основанный на сокращении повторных вычислений вейвлетов. Сокращение вычислений достигается за счет учета инвариантности вейвлетов относительно сдвига. Таким образом, вычислив один раз ненулевые значения вейвлетов для всех масштабов и сохранив их, достаточно обращаться по номеру к значению, соответствующему номеру сдвига. Разработанные алгоритмы реализованы в виде комплекса программ. Показано, что предложенный алгоритм работает быстрее классического и без значительной потери точности вычислений.
| Authors: A.A. Stolbova (anastasiya.stolbova@bk.ru) - Samara National Research University (Assistant), Samara, Russia | |
| Keywords: norm of the wavelet, radius of the wavelet, continuous wavelet transformation |
|
| Page views: 7930 |
PDF version article Full issue in PDF (29.80Mb) |
| Permanent link: http://swsys.ru/index.php?page=article&id=4381&lang=en |
PDF version article Full issue in PDF (29.80Mb) |
| The article was published in issue no. № 4, 2017 [ pp. 765-769 ] |
Perhaps, you might be interested in the following articles of similar topics:
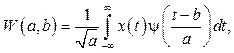 (1)
(1) , (2)
, (2)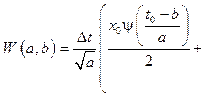
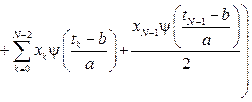 , (3)
, (3)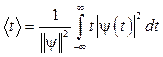 – центр,
– центр, – радиус,
– радиус,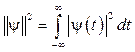 – норма вейвлета.
– норма вейвлета.
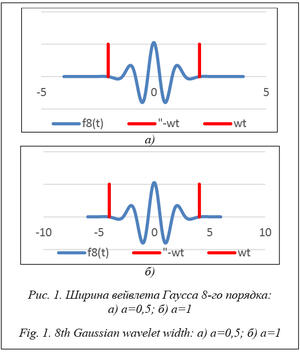
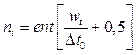 , где ent[] – операция взятия целой части; Dt0 – интервал дискретизации вейвлета.
, где ent[] – операция взятия целой части; Dt0 – интервал дискретизации вейвлета. , где
, где 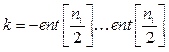 .
.
 ,
,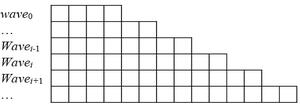
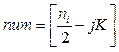 , где ni – число отсчетов i-го вейвлета; K – шаг сдвига.
, где ni – число отсчетов i-го вейвлета; K – шаг сдвига.
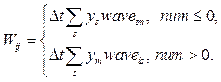

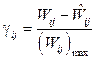 , где W – точное значение коэффициента;
, где W – точное значение коэффициента;  – оценка коэффициента.
– оценка коэффициента.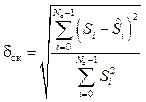 ,
, – оценка скейлограммы.
– оценка скейлограммы.
