Построение эффективных радиолокационных систем распознавания (РЛСР) невозможно без использования методов математического моделирования. Сутью математического моделирования РЛСР являются описания физических процессов формирования локационных сигналов, приема отраженных сигналов и их обработка для определения координатных и некоординатных признаков наблюдаемых объектов, а также процессов распознавания на основе получаемой модельной апостериорной информации на языке математики: формул, аналитических соотношений, уравнений и алгоритмов. Результатом подобных описаний яв- ляется построение комплекса математических моделей, представляющего собой инструмент для организации исследований, основанных на проведении целенаправленных математических экспериментов [1].
Математическая модель позволяет оценить эффективность РЛСР еще на ступени ее разработки и проектирования. Для математического моделирования необходимо построить специальную статистическую модель, на которой реализуется многократное повторение процесса распознавания объектов каждого класса. Модель должна позволять оценивать значения критерия эффективности в зависимости от состава алфавита классов при данном словаре признаков и, наоборот, при данном алфавите классов – в зависимости от объема апостери- орной информации, то есть конкретного словаря признаков. Модель должна обеспечивать возможность оценки влияния на значение критерия эффективности системы того или иного сокращения рабочего словаря признаков по сравнению с априорным, погрешностей измерения признаков, ошибок априорного описания классов на языке признаков предполагаемого рабочего словаря [1].
Цель – разработка математической модели РЛСР и программы для ЭВМ, позволяющей оценить ее эффективность в зависимости от различных факторов, в том числе от технических характеристик радиолокационного канала измерения признаков.
Общую модель РЛСР можно представить двумя группами основных моделей. Первая охватывает процессы измерения признаков, вторая предназначена для исследования процедуры распознавания и оценки эффективности РЛСР. В качестве третьей, дополнительной, модели в работе реализована модель оценки качества признаков распознавания.
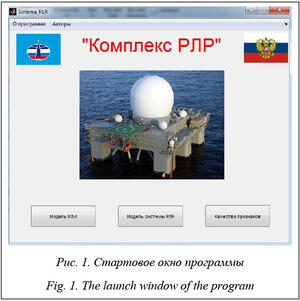
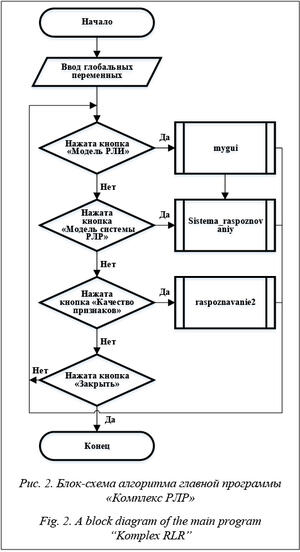 В результате проведенных исследований создана программа «Комплекс РЛР» (РЛР – радилокационное распознавание), представляющая собой приложение MATLAB с графическим интерфейсом, содержащее элементы управления, оси для вывода графиков и текстовые области для ввода исходных данных и выводы результатов (рис. 1). Блок-схема главного алгоритма программы пред- ставлена на рисунке 2.
В результате проведенных исследований создана программа «Комплекс РЛР» (РЛР – радилокационное распознавание), представляющая собой приложение MATLAB с графическим интерфейсом, содержащее элементы управления, оси для вывода графиков и текстовые области для ввода исходных данных и выводы результатов (рис. 1). Блок-схема главного алгоритма программы пред- ставлена на рисунке 2.
Модель радиолокационных измерений
Модуль «Модель РЛИ» (подпрограмма mugui) является математической моделью системы радиолокационных измерений (РЛИ). Модель имитирует процесс обнаружения, сопровождения по дальности и измерения эффективной поверхности рассеяния (ЭПР) объекта, а также позволяет оценить отношение сигнал/шум, дисперсию и среднее квадратичное отклонение (СКО) ошибки измерения ЭПР цели по формуле Крамера–Рао для амплитуды сигнала, считая, что ЭПР и амплитуда отраженного сигнала являются пропорциональными величинами.
Модель позволяет оценить влияние тактико-технических характеристик (ТТХ) радиолокационной системы (РЛС) на ошибку РЛИ.
В алгоритме работы программы сначала рассчитывается максимальная дальность радиолокационного обнаружения для РЛС с ТТХ и для объекта с ЭПР, введенными пользователем или заданными в программе:
 . (1)
. (1)
Далее рассчитывается отношение сигнал/шум для интервала дальностей от Rmin, заданной в ТТХ РЛС, до Rmax:
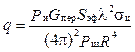 . (2)
. (2)
В РЛСР для принятия решений используют измерения, полученные с помощью РЛС, причем точность таких измерений оказывает непосредственное влияние на эффективность работы системы распознавания.
При определении точностных характеристик систем и синтеза их оптимальных схем внимание прежде всего уделяется анализу потенциальных ошибок, так как они позволяют выявить основные требования к структуре сигналов и алгоритмам их обработки. Потенциальная ошибка измерения ЭПР цели, считая, что ЭПР и амплитуда отраженного сигнала – пропорциональные величины [2]:
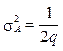 . (3)
. (3)
Разработанный алгоритм позволяет имитировать процесс сопровождения цели по дальности, вычислять значение ЭПР по результатам не только единичного замера, но и в зависимости от количества зондирований. Программа рассчитывает ЭПР цели в каждом зондировании и усредненное значение по всему циклу сопровождения, как на реальных РЛС, а также позволяет графически увидеть зависимость ошибок измерений от отношения сигнал/шум, как функции от дальности и от количества зондирований.
Разработанный алгоритм моделирования РЛИ включает в себя следующее.
1. Ввод исходных данных в виде технических характеристик радиолокационного канала, времени сопровождения и параметров наблюдаемого объекта.
2. Вычисление максимальной дальности обнаружения объекта РЛС с введенными ТТХ.
3. Вычисление зависимости отношения сигнал/шум на выходе согласованного фильтра от дальности при оптимальном методе обработки без учета потерь в приемном тракте.
4. Вычисление зависимости дисперсии и СКО ошибок измерения ЭПР объекта в зависимости от дальности.
5. Моделирование процесса обнаружения и сопровождения объекта, расчет его измеренного ЭПР с учетом ошибок.
6. Вывод результатов в виде графиков и текста на экран.
Таким образом, на выходе модели рассчитывается оценка измеренной ЭПР цели, что обусловливается наличием ошибок, в том числе зависящих от ТТХ РЛС. Измеренное значение математического ожидания значения ЭПР цели и дисперсия ошибки ее измерения используются в модуле «Модель системы РЛР» для оценки эффективности СРЛР.
Модель системы распознавания
 Модуль «Модель системы РЛР» (подпрограмма Sistema_raspoznavaniy) предназначен для оценки эффективности работы СРЛР при двухклассовом распознавании по признаку «измеренное ЭПР цели» в зависимости от априорных исходных данных и является статистической моделью системы распознавания (рис. 3). Полученное в результате статистических испытаний (метод Монте-Карло) множество случайных исходов решения задачи распознавания позволяет, используя методы математической статистики, определять искомые оценки для вероятностей правильных и ошибочных решений и, таким образом, оценивать зависимость этих вероятностей от условий функционирования системы, а значит, и от технических характеристик проектируемой РЛС. Тем самым в процессе разработки последней обеспечивается возможность так скорректировать ее характеристики, чтобы на выходе системы обеспечить надлежащее значение критерия эффективности [1].
Модуль «Модель системы РЛР» (подпрограмма Sistema_raspoznavaniy) предназначен для оценки эффективности работы СРЛР при двухклассовом распознавании по признаку «измеренное ЭПР цели» в зависимости от априорных исходных данных и является статистической моделью системы распознавания (рис. 3). Полученное в результате статистических испытаний (метод Монте-Карло) множество случайных исходов решения задачи распознавания позволяет, используя методы математической статистики, определять искомые оценки для вероятностей правильных и ошибочных решений и, таким образом, оценивать зависимость этих вероятностей от условий функционирования системы, а значит, и от технических характеристик проектируемой РЛС. Тем самым в процессе разработки последней обеспечивается возможность так скорректировать ее характеристики, чтобы на выходе системы обеспечить надлежащее значение критерия эффективности [1].
В качестве решающего правила в модели используется байесовская теория решений. Классификатор или решающее правило относит объект к одному из классов по его вектору признаков. Одним из преимуществ байесовского классификатора является его оптимальность по отношению к минимизации ошибки классификации. Недостатком метода является необходимость знания априорных данных об объектах, что не всегда возможно.
Для работы байесовского классификатора необходимо задание первоначальных условий: вероятности появления целей разных классов P(ωj), условные плотности распределений признака для разных классов p(x|ωj) и матрица потерь [3].
Пусть значения признака распознавания x в каждом классе подчинены нормальным законам распределения с математическими ожиданиями m1 и m2 и средними квадратичными отклонениями σ1 и σ2 соответственно:
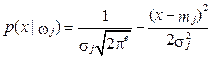 . (4)
. (4)
Правило Байеса показывает, как наличие измеренной величины x позволяет из априорной вероятности P(ωj) получить апостериорную вероятность:
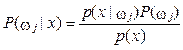 , (5)
, (5)
где .
.
В этом случае решение принимается в пользу того класса, для которого апостериорная вероятность P(ωj|x) будет больше.
Исходя из заданной пользователем программы матрицы потерь рассчитываются значения условного среднего риска:
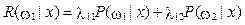 ,
,
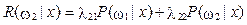 .
.
Решение принимается в пользу класса, для которого условный риск имеет минимальное значение.
В программе реализована возможность моделирования как объектов только одного или второго класса, так и случайного набора объектов двух классов.
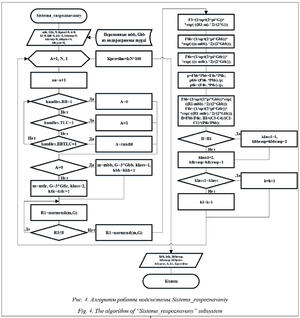 Блок-схема алгоритма подпрограммы моделирования системы распознавания Sistema_raspoznavaniy представлена на рисунке 4.
Блок-схема алгоритма подпрограммы моделирования системы распознавания Sistema_raspoznavaniy представлена на рисунке 4.
Модель оценки качества признаков распознавания
На практике при разработке систем распознавания достаточно часто возникает задача сравнительной оценки качества признаков. Это необходимо для составления рабочего словаря признаков из априорного для определения весовых коэффициентов каждого признака в общей задаче РЛР. К тому же оценка позволяет сократить количество признаков, отбросив наиболее неэффективные при ограничении на вычислительные ресурсы. В общем случае задача разработки рабочего словаря признаков системы распознавания сводится к тому, чтобы в пределах выделенных ресурсов определить перечень технических средств, создание которых обеспечивает измерение наиболее информативных признаков априорного словаря.
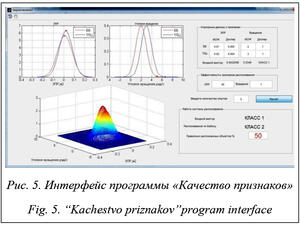
Модуль «Качество признаков» предназначен для исследования влияния качества (информативности) признаков на вероятность получения правильных решений системой распознавания (рис. 5).
Качество (информативность) выше у тех признаков, для которых объекты разных классов располагаются на большем удалении друг от друга по оси признака.
 Для сравнительной оценки эффективности при- знаков используется величина
Для сравнительной оценки эффективности при- знаков используется величина
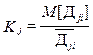 , (6)
, (6)
где M[Дji] – математическое ожидание дисперсии j-го признака i-го класса; 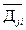 – дисперсия математического ожидания распределения признаков при переходе от класса к классу [4].
– дисперсия математического ожидания распределения признаков при переходе от класса к классу [4].
Величины, входящие в (6), имеют вид:
 , (7)
, (7)
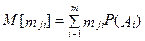 , (8)
, (8)
где P(Ai) – априорная вероятность появления i-го класса объектов.
Тогда наиболее эффективным является признак, который обеспечивает
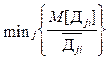 . (9)
. (9)
Результат работы программы – расчет эффективности системы распознавания в зависимости от качества выбранных признаков распознавания. Наилучшие результаты эффективности работы системы распознавания получаются для признаков с минимальным отношением, рассчитанным по формуле (9).
Таким образом, в ходе проведенной работы создана и программно реализована математическая модель РЛСР, позволяющая проводить исследова- ния ее эффективности в зависимости от различных факторов. Адекватность модели проверена по кор- ректности отражаемой ею концептуальной модели путем подачи на ее вход заведомо известного вектора и сравнения отклика системы с ожидаемым. На программный комплекс получено свидетельство о государственной регистрации программы для ЭВМ.
Литература
1. Горелик А.Л., Барабаш Ю.Л., Кривошеев О.В., Эпштейн С.С. Селекция и распознавание на основе локационной информации. М.: Радио и связь, 1990. 240 с.
2. Слока В.К. Вопросы обработки радиолокационных сигналов. М.: Сов. радио, 1970. 255 с.
3. Дуда Р., Харт П. Распознавание образов и анализ сцен. М.: Мир, 1976. 511 с.
4. Горелик А.Л., Скрипкин В.А. Методы распознавания. М.: Высш. шк., 1977. 222 с.
5. Дасгупта С., Пападимитриу Х., Вазирани У. Алгоритмы; [пер. с анг. под ред. А. Шеня]. М.: Изд-во МЦНМО, 2014. 320 с.
6. Хрестинин Д.В., Богомаз Д.В., Покора А.Ф., Трофи- мов М.О. Модель системы радиолокационного распознавания: свид. № 2015663387. Рос. Федерация. № 2015619508; заявл. 28.09.2015; опубл. 16.12.2015.
7. Теоретические основы радиолокации; [под ред. В.Е. Дулевича]. М.: Сов. радио, 1964. 732 с.
8. Сколник М. Введение в технику радиолокационных систем. М.: Мир, 1965. 747 с.
9. Фукунага К. Введение в статистическую теорию распознавания образов; [пер. с англ.]. М.: Наука, 1979. 368 с.
10. Местецкий Л.М. Математические методы распознавания образов. М.: Изд-во МГУ, 2004. 85 с.
References
- Gorelik A.L., Barabash Yu.L., Krivosheev O.V., Epshtein S.S. Selektsiya i raspoznavanie na osnove lokatsionnoy informatsii [Selection and Recognition Based on Radar Information]. Moscow, Radio i svyaz Publ., 1990, 240 p.
- Sloka V.K. Voprosy obrabotki radiolokatsionnykh signalov [Processing of Radar Signals]. Moscow, Sovetskoe radio Publ., 1970, 255 p.
- Duda R., Khart P. Raspoznavanie obrazov i analiz stsen [Pattern Recognition and Scene Analysis]. Moscow, Mir Publ., 1976, 511 p.
- Gorelik A.L., Skripkin V.A. Metody raspoznavaniya [Recognition Methods]. 3rd ed., Мoscow, Vysshaya shkola Publ., 1977, 222 p.
- Dasgupta S., Papadimitriou C.H., Vazirani U. Algorithms. McGraw-Hill Publ., 2006, 336 p. (Russ. ed.: Мoscow, МTsNМO Publ., 2014, 320 p.).
- Khrestinin D.V., Bogomaz D.V., Pokora A.F., Trofimov M.O. Model sistemy radiolokatsionnogo raspoznavaniya [The Model of Radar Recognition System]. Certificate no. 2015663387, Russian Federaton. No. 2015619508, cl. 28/09/2015, publ. December 16, 2015.
- Teoreticheskie osnovy radiolokatsii [Theoretical Basis of Radar Detection]. V.E. Dulevich (Ed.), Moscow, Sovetskoe radio Publ., 1964, 732 p.
- Skolnik M. Vvedenie v tekhniku radiolokatsionnykh sistem [Introduction to Radar Systems]. Moscow, Mir Publ., 1965, 747 p.
- Fukunaga K. Introduction to statistical pattern recognition. Academic Press, NY, 1972 (Russ. ed.: Мoscow, Nauka Publ., 1979, 368 p.).
- Mestetsky L.M. Matematicheskie metody raspoznavaniya obrazov [Mathematical Methods of Pattern Recognition]. Moscow State Univ. Publ., 2004, 85 p.


 . (1)
. (1)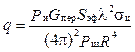 . (2)
. (2)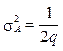 . (3)
. (3)
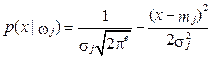 . (4)
. (4)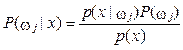 , (5)
, (5) .
.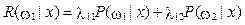 ,
,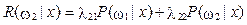 .
.

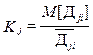 , (6)
, (6)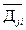 – дисперсия математического ожидания распределения признаков при переходе от класса к классу [4].
– дисперсия математического ожидания распределения признаков при переходе от класса к классу [4]. , (7)
, (7)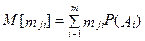 , (8)
, (8)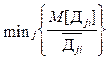 . (9)
. (9)