Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Косвенный метод нечеткого вывода для продукционных систем со многими входами
Аннотация:
Abstract:
| Авторы: Синюк В.Г. (lysevi@gmail.com) - Белгородский государственный технологический университет им. В.Г. Шухова, Северо-Кавказский филиал, г. Минеральные Воды, кандидат технических наук, Куценко Д.А. () - | |
| Ключевые слова: продукционная система, нечеткий вывод, моделирование |
|
| Keywords: expert system, fuzzy conclusion, modeling |
|
| Количество просмотров: 16008 |
Версия для печати Выпуск в формате PDF (1.92Мб) |
Рассмотрим систему с n входами Пусть заданы нечеткие множества Рассмотрим правило modus ponens следующего вида. Предпосылка: Правило:
Вывод: Чтобы получать выход В методе Заде (называемом прямым методом) правило
где В методах Болдуина и Цукамото (называемых косвенными методами) сначала определяется нечеткое значение истинности антецедента
Затем вычисляется нечеткое значение истинности для консеквента
В методе Болдуина
В методе Цукамото нечеткое значение истинности для высказывания «Если
и
Пусть зависимость между входами и выходом описывается нечеткими правилами «Если-то» Hk: где k – номер правила в системе, Рассмотрим алгоритм решения поставленной задачи для правил вида (7) на основе метода вывода Цукамото в виде следующей последовательности этапов. Агрегирование Для k-го правила (
где
при где T – Т-норма; S – S-конорма. В качестве T и S можно использовать различные n-местные Т-нормы и S-конормы, например, минимум
Если множества
где
Если входы имеют различную важность, тогда функция принадлежности нечеткой степени истинности (10) имеет следующий вид:
для Активизация Для k-го правила (
при Нечеткое значение истинности импликации
где В этом случае нечеткий логический вывод соответствует косвенному методу вывода Болдуина. Аккумуляция Для k-го правила (
Значение выходной переменной
Если консеквент правила представлен в виде одноточечного множества, то есть
то нечеткое значение выходной переменной
Аналогичным образом можно рассчитать нечеткое значение выходной переменной
Дефаззификация Четкое значение выходной переменной Преимущество рассмотренного метода нечеткого вывода по сравнению с композиционным правилом вывода заключается в том, что вычисления переносятся в пространство нечетких значений истинности. Это позволяет уйти от предметной области и использовать универсальное представление для выражения таких вербальных понятий, как «истинно», «очень истинно» и т.п. На основе данной системы нечеткого вывода можно построить нейро-нечеткую систему. Дальнейшие исследования связаны с разработкой специально адаптированного для данной задачи генетического алгоритма, с помощью которого реализуются процессы обучения и настройки нейро-нечеткой системы. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=97&lang=&like=1 |
Версия для печати Выпуск в формате PDF (1.92Мб) |
| Статья опубликована в выпуске журнала № 1 за 2008 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Программная система исследований динамики технологических процессов формования химических волокон
- Информационно-вычислительная система моделированияи прогнозирования торфяных пожаров
- Моделирование информационных процессов систем управления большими данными для решения задач кибербезопасности
- Алгоритм и программа расчета напряженно-деформированного состояния песчаных грунтов при циклическом нагружении
- Программа идентификации условий теплообмена для изделий плоской формы
Назад, к списку статей



 (5)
(5) (7)
(7)

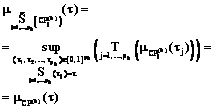
 (12)
(12) . (15)
. (15) . (16)
. (16)