Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Authors: (byg@yandex.ru) - , Ph.D, (midli@mail.ru) - , Ph.D | |
| Ключевое слово: |
|
| Page views: 14166 |
Print version Full issue in PDF (1.13Mb) |
Целью настоящей статьи является изложение результатов сравнительного анализа разработанного авторами алгоритма распознавания, реализующего методы адаптивной нечеткой логики с известными алгоритмами – методом эталонов и нейросетевым с использованием сети встречного распространения. Подобный анализ проводился путем реализации имитационного эксперимента в среде математической системы MATLAB [1]. Сравнение алгоритмов проводилось путем сопоставления количества ошибок распознавания при обучающих и тестовых выборках, одинаковых для всех алгоритмов. Процедура построения (обучения) предлагаемого нечеткого адаптивного распознавателя выглядит следующим образом. 1. Из m (m (возможно, с учетом имеющейся априорной информации) обучающей выборки составляется начальная база знаний распознавателя, отображаемая матрицей Um´(n+S) со строками вида ( Такое представление полагается эквивалентным набору нечетких правил: Pi: если … и и где
или двойной экспоненциальной формы
симметричные относительно центров
где 2. Для всех примеров обучающей выборки рассчитываются прогнозируемые значения
Четкое значение переменных вывода (с учетом их отмеченной бинарности) определяется при этом с помощью дискретного варианта центроидного метода:
Далее проверяется условие останова процедуры
где e>0 – заданное значение ошибки распознавателя. При выполнении неравенства – переход к п. 5 процедуры. 3. Для каждой новой экспериментальной точки (из числа точек, не вошедших в базу знаний) по соотношениям (5), (6) рассчитываются прогнозируемые значения
При его выполнении база знаний распознавателя пополняется путем добавления в матрицу U строки ( 4. Выполняется параметрическая оптимизация нечетких правил путем решения оптимизационной задачи
Принимается, что теперь функции принадлежности текущей базы правил зависят от найденного нового (оптимального) вектора параметров a. Осуществляется переход к п.2 процедуры, если только m 5. Конец процедуры. Вывод информации об элементах матрицы U и вектора a. Предлагаемая авторами процедура построения распознавателя обладает следующими свойствами: а) обеспечивает генерацию взаимно непротиворечивых правил; б) относится к классу процедур адаптивной нечеткой логики и обеспечивает получение оценки разделяющей функции в виде обобщенной регрессии; в) данная оценка идентична функции, восстанавливаемой обобщенно-регрессионной нейронной сетью (сетью GRNN) [1]; г) от процедур непараметрической регрессии и отмеченного нейросетевого подхода предложенная процедура отличается способом формирования базы знаний, в том числе за счет использования имеющейся априорной информации, а также наличием промежуточного этапа параметрической оптимизации; д) указанное формальное сходство с непараметрической регрессией и обобщенно-регрессионной нейронной сетью позволяет определить асимптотические свойства распознавателя: в случае разделимых классов при увеличении объема обучающей выборки вероятность ошибки распознавания стремится к нулю. Сравним работоспособность предложенного метода распознавания и его точность с нейросетевым методом и методом эталонов для различных случаев расположения объектов двух образов. Предварительно отметим, что процесс распознавания при известных U, a, m и заданном x отображается формулами (2) (или (3)), (5), (6). В качестве инструментального средства для проведения имитационного эксперимента была выбрана математическая система MATLAB. Это было сделано из следующих соображений: MATLAB сочетает в себе язык программирования высокого уровня для технических вычислений, наличие целого ряда пакетов и библиотек расширения системы (например, пакета оптимизации Optimization Toolbox, пакета нечеткой логики Fuzzy Logic, пакета расширения по нейронным сетям), наличие инструментальных средств для разработки графического интерфейса пользователя (GUI-интерфейса) и сервера независимо исполняемых приложений (Runtime Server). Для сравнения методов распознавания использовался созданный авторами комплекс программ в системе MATLAB. Комплекс программ состоит из следующих компонентов: - приложения с окном графической визуализации результатов для создания обучающей и тестовой выборки и сохранения ее в виде внешних файлов (с расширениями *.obv, и *.tsv); - приложений с реализацией классификатора на основе метода эталонов, классификатора с применением нейронной сети встречного распространения (для сравнения с описанным выше адаптивным нечетким распознавателем) с окном графической визуализации результатов; - приложения с реализацией адаптивного нечеткого распознавателя с окном графической визуализации результатов. Для распознавания в качестве модельных были выбраны примеры с двумя образами, объекты которых моделировались с использованием датчиков (функций) случайных чисел, распределенных по нормальному закону. Объекты характеризовались двумя независимыми признаками
Обучающие выборки для всех примеров имели по 12, а тестовые по 1000 объектов. Результаты моделирования отражены в таблице, в клетках которой указано количество ошибочно классифицированных объектов тестовых выборок.
Заметим, что чисто теоретический анализ погрешностей распознавателя в данной ситуации провести невозможно.
Выполненный сравнительный анализ показал высокую эффективность алгоритма распознавания, построенного на основе методов адаптивной нечеткой логики. Отметим, что в процессе реализации машинного эксперимента авторами была отработана недокументированная в известных источниках методика построения программных комплексов и GUI-приложений в среде MATLAB в сочетании с использованием имеющегося базового набора функций специализированных пакетов расширений. Список литературы 1. Дьяконов В.П., Абраменкова И.В., Круглов В.В. MATLAB 5.3.1 с пакетами расширений. - М.: Нолидж,- 2001. 2. Круглов В.В., Борисов В.В. Гибридные нейронные сети. - Смоленск.: Русич, 2001. 3. Круглов В.В., Борисов В.В. Искусственные нейронные сети. Теория и практика. - М.: Горячая линия – Телеком, 2001. |
| Permanent link: http://swsys.ru/index.php?page=article&id=706&lang=&lang=&like=1&lang=en |
Print version Full issue in PDF (1.13Mb) |
| The article was published in issue no. № 2, 2002 |
Perhaps, you might be interested in the following articles of similar topics:
- Программные средства автоматизации приборостроительного производства изделий радиоэлектронной аппаратуры
- Формулировка задачи планирования линейных и циклических участков кода
- Система поддержки принятия решений по планированию профессиональной структуры подготовки специалистов
- Автоматизированная информационная система маркетолога
- Правовая охрана программного обеспечения с точки зрения международного сотрудничества стран-членов СЭВ
Back to the list of articles
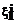 ,
,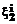 , … ,
, … , 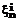 ,
, 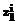 ,
, 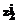 , … ,
, … , 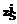 ),
), 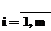 , где
, где 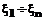 – количественные признаки образов (компоненты вектора признаков
– количественные признаки образов (компоненты вектора признаков 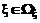 );
); 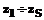 – индикаторы образов, принимающие значения +1 или –1 и образующие вектор Z; S – общее количество распознаваемых образов.
– индикаторы образов, принимающие значения +1 или –1 и образующие вектор Z; S – общее количество распознаваемых образов.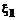 есть
есть 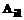 и
и 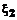 есть
есть 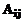 и …
и …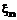 есть
есть 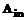 , то
, то 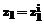 и
и 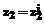 и …
и …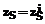 ,
, 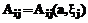 – функция принадлежности колоколообразной
– функция принадлежности колоколообразной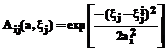 (2)
(2)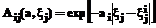 , (3)
, (3)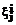 , ai – параметры данных функций (компоненты вектора a), для начальной базы правил выбираемые в соответствии с рекомендациями [2], например, для функции (2) как
, ai – параметры данных функций (компоненты вектора a), для начальной базы правил выбираемые в соответствии с рекомендациями [2], например, для функции (2) как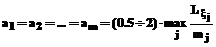 , (4)
, (4)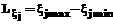 , mj – количество функций принадлежности, ассоциированных с
, mj – количество функций принадлежности, ассоциированных с  .
.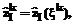
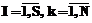 в соответствии с алгоритмом нечеткого вывода Сугэно нулевого порядка [1-3] с тем отличием от классического варианта данного алгоритма, что степень истинности предпосылки каждого правила находится как нечеткая импликация в форме Ларсена, то есть как произведение
в соответствии с алгоритмом нечеткого вывода Сугэно нулевого порядка [1-3] с тем отличием от классического варианта данного алгоритма, что степень истинности предпосылки каждого правила находится как нечеткая импликация в форме Ларсена, то есть как произведение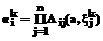 . (5)
. (5)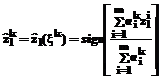 . (6)
. (6)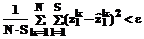 , (7)
, (7)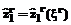 и проверяется неравенство
и проверяется неравенство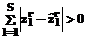 . (8)
. (8)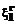 ,
,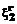 , … ,
, … , 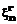 ,
, 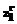 ,
, 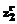 , … ,
, … , 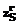 ). В противном случае матрица U остается без изменений.
). В противном случае матрица U остается без изменений.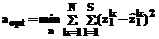 . (9)
. (9)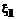 и
и 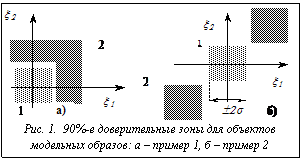 Разумеется, во многих случаях погрешность распознавания зависит и от типа распознавателя. Так, для ситуаций, отображенных на рисунке 1, практически неработоспособным будет метод эталонов, значительно хуже отрабатывает нейросетевой метод и хорошие результаты дает разработанный авторами адаптивный нечеткий распознаватель.
Разумеется, во многих случаях погрешность распознавания зависит и от типа распознавателя. Так, для ситуаций, отображенных на рисунке 1, практически неработоспособным будет метод эталонов, значительно хуже отрабатывает нейросетевой метод и хорошие результаты дает разработанный авторами адаптивный нечеткий распознаватель. Сравнение приведенных результатов, по крайней мере на рассмотренных модельных примерах, показывает очевидное преимущество разработанного распознавателя.
Сравнение приведенных результатов, по крайней мере на рассмотренных модельных примерах, показывает очевидное преимущество разработанного распознавателя.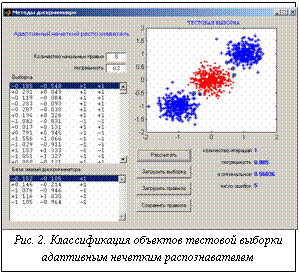 На рисунке 2 приведен пример функционирования разработанного комплекса программ – результат распознавания объектов с помощью одного из классификаторов (созданного по разработанному и описанному выше алгоритму адаптивного нечеткого распознавателя) – для заранее заданных и обсужденных выше проблемных областей.
На рисунке 2 приведен пример функционирования разработанного комплекса программ – результат распознавания объектов с помощью одного из классификаторов (созданного по разработанному и описанному выше алгоритму адаптивного нечеткого распознавателя) – для заранее заданных и обсужденных выше проблемных областей.