Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Инструментальные и программные средства построения сетевых моделей
Аннотация:
Abstract:
| Автор: Сенькина М.А. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 17567 |
Версия для печати Выпуск в формате PDF (1.31Мб) |
Все более широкое применение находят методы автоматизации управления проектами. В их числе системы сетевого планирования и управления (СПУ), основой которых является сетевая модель. Эти системы позволяют решать задачи оптимизации по времени и стоимости, распределения ограниченных ресурсов проекта и, в конечном счете, построения календарного плана выполнения работ. Очевидно, что от степени адекватности сетевой модели зависит качество управления проектом. Вместе с тем построение сетевой модели – достаточно трудоемкий процесс, фактически не имеющий формализованных правил синтеза топологии сети. Известны отдельные теоретические и практические работы по автоматизации построения сетевых моделей [2], но применяемый в них подход практически не снижает трудоемкости построения сетей и не обеспечивает необходимой степени адекватности модели. В связи с практической актуальностью проблемы в данной работе рассматриваются вопросы разработки и обоснования алгоритмов построения сетевых моделей и структура программного комплекса. Частично эти вопросы представлены в работах [1,3]. Алгоритмы синтеза топологии сетевых моделей Пусть задан граф G=[P,R], состоящий из множества вершин P и множества дуг Дуги Ориентированный граф с введенным на нем отношением частичного порядка на множестве дуг будем обозначать [G,≤]. Такой граф можно описать матрицей, введя в рассмотрение функцию вида:
Матрица А определяется через (1) в виде: Назовем бинарную матрицу А порядка N, где N=|R|, матрицей следования ориентированных дуг. Из (1) следует, что Элементы Следовательно, функция (1) обладает свойством:
Процесс изменения значений элементов неполной матрицы следования дуг на основе свойства (2) будем называть корректировкой. Сформулируем положения, лежащие в основе алгоритмов автоматизированного проектирования топологии сетевых моделей. Теорема 1. Пусть [G,≤] – ориентированный граф, имеющий цикл Доказательство. Из определения частичного порядка на множество дуг имеем: Следствие 1. Петля является циклом единичной длины. При наличии в ориентированном графе петли Следствие 2. В ориентированном ациклическом графе диагональные элементы полной матрицы следования дуг равны нулю. Теорема 2. Пусть [G,≤] – ориентированный ациклический граф, А – соответствующая ему полная матрица следования дуг, S – матрица смежности дуг и Е – единичная матрица того же порядка. Утверждается, что если Предварительно докажем следующую лемму. Лемма 1. Пусть А – полная матрица следования дуг ациклического ориентированного графа [G,≤]. Тогда матрица С=А×А определяет число дуг, заключенных между любыми двумя дугами. Доказательство. Элементы матрицы С вычисляются по формуле: Поскольку А – бинарная матрица, то Следствие 3. Элементы 1) если дуга 2) если дуги 3) если дуга Перейдем к доказательству теоремы 2. Рассмотрим матрицу В=С+А=A2+А=А(А+Е). Ее элементы Если Следствие 4. Если дуга Теорема 3. Пусть А – матрица следования дуг ориентированного ациклического графа [G,≤], Е – единичная матрица того же порядка. Утверждается, что если элементы
где Предварительно докажем следующую лемму. Лемма 2. Пусть Тогда матрица Доказательство. Элементы
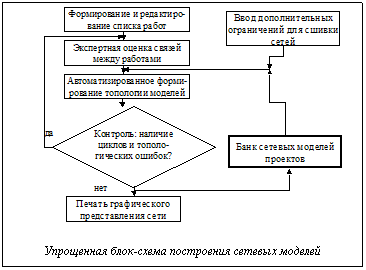
Если дуги Если Перейдем к доказательству теоремы. При n=1 имеем В=А+Е, С=В, D=А. При n=2, обозначив На основании доказанных положений предлагается алгоритм контроля и корректировки матрицы следования ориентированных дуг и получения матрицы смежности дуг ориентированного ациклического графа. 1. Если 2. Присваиваем 3. Вычисляем 4. Если 5. Если 6. Вычисляем 7. Если S2=S1 (условие окончания процесса корректировки), то переходим к п. 8. Иначе S1=S2 и переходим к п. 4. 8. Вычисляем 9. Для всех 10. Если 11. Печать полученных результатов. Структура программного комплекса Укрупненная блок-схема комплекса представлена на рисунке. Она включает в себя программные модули, обеспечивающие ввод и редактирование данных, построение сети и ее корректировку, а также модуль сшивки сетей различных проектов в единую сеть.
Работа над новым проектом начинается с редактирования списка работ. В случае необходимости в проект можно включать ранее разработанные сетевые модели. Работы включаемого проекта будут занесены в конец списка с сохранением связей между ними, что значительно экономит время разработки и повышает качество проекта. После завершения редактирования списка работ можно перейти непосредственно к построению сети. Процесс идет в интерактивном режиме. Необходимым и достаточным условием построения адекватной сетевой модели является определение экспертом основных связей. Данный этап является самым ответственным при работе с программой, а качество сети будет определяться квалификацией эксперта. После завершения оценки связей для текущей работы программа вводит дополнительные связи между работами, используя условия транзитивности. Это значительно уменьшает время подготовки исходных данных. Случайные ошибки эксперта могут привести к образованию циклов. Поэтому предусмотрена проверка сети на наличие циклов и петель и их автоматическое разрушение. Эксперту выдается сообщение о возникновении цикла и список работ, образовавших его. Когда все связи между работами установлены, выдается соответствующее сообщение и формируется сетевой график. Сетевая модель представляется в виде графа – «работы-дуги», при необходимости вводятся фиктивные работы. Сетевой график формируется автоматически. Случайную ошибку можно оперативно исправить в режиме редактирования. Полученную сетевую модель можно распечатать, сохранить и в дальнейшем использовать в качестве основы для других проектов или сшивать с другими проектами. Программа написана на языке Visual C++. Она отвечает современным требованиям пользовательского интерфейса, имеет подробную справку по всем этапам работы. Количество работ в проекте зависит от размера оперативной памяти компьютера. На современном компьютере программа позволяет создавать проекты, включающие более 1000 работ. Программа апробирована в строительстве, при разработке бытовых и научно-технических проектов. Временная оценка показала, что автоматизация построения сетевого графика позволяет сократить время более чем на 80%. При этом сетевая модель, полученная программным путем, более полно удовлетворяет принципу максимальной независимости работ, чем построенная вручную [1]. В заключение отметим, что целесообразна разработка пакета прикладных программ для управления проектами. Он должен включать в себя автоматическое формирование топологии сети, расчет ее временных параметров и решение оптимизационных и распределительных задач. Список литературы 1. Ильягуев П.М. К вопросу построения сетевых моделей. / В сб.: Совершенствование хозяйственного механизма и рациональное использование ресурсов. – Махачкала: - Даг. ФАН СССР. - 1985. - С. 163 – 189. 2. Егоров О.П. Комплекс программ автоматизированного построения сетевых структур (Инв. № П007295) // Информ. бюллетень: Алгоритмы и программы. – М.: ВНТИЦ, 1989. 3. Ильягуев П.М., Сенькина М.А., Бережной Д.А. Экспертная система автоматизации построения сетевых моделей. // Матер. Республик. науч.-практ. конф.: Информационные и телекоммуникационные системы: состояние и перспективы развития. – Махачкала: РАН ДНЦ. – 2001. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=570&lang=&lang=&like=1 |
Версия для печати Выпуск в формате PDF (1.31Мб) |
| Статья опубликована в выпуске журнала № 4 за 2004 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Формулировка задачи планирования линейных и циклических участков кода
- Расчет нечеткого сбалансированного показателя в задачах взвешивания терминов электронных документов
- Учебно-исследовательский программно-лабораторный комплекс NET_LAB
- Системное тестирование программных изделий
- Основные характеристики методики АДЕСА-2 для разработки информационных систем и возможности ее практического применения
Назад, к списку статей



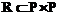 . Будем считать, что вершина
. Будем считать, что вершина 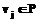 достижима из вершины
достижима из вершины  , если существует путь
, если существует путь 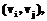
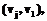
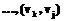 из
из 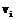 в
в  и обозначать
и обозначать 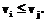 Геометрически это означает, что, двигаясь по дугам графического изображения графа, можно из
Геометрически это означает, что, двигаясь по дугам графического изображения графа, можно из 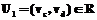 достижима из дуги
достижима из дуги 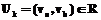 , если
, если 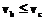 и обозначать
и обозначать 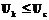 . Данное определение также удовлетворяет требованиям, предъявляемым отношениям частичного порядка. Геометрическая интерпретация частичного порядка на множестве дуг – это существование пути из конечной вершины
. Данное определение также удовлетворяет требованиям, предъявляемым отношениям частичного порядка. Геометрическая интерпретация частичного порядка на множестве дуг – это существование пути из конечной вершины 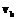 дуги
дуги 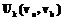 в начальную вершину
в начальную вершину 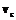 дуги
дуги  .
.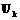 и
и  будем называть сравнимыми, если будет верно одно из следующих соотношений:
будем называть сравнимыми, если будет верно одно из следующих соотношений: 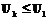 или
или 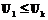 , в противном случае они несравнимы.
, в противном случае они несравнимы.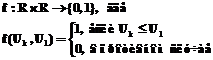 . (1)
. (1)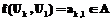 .
.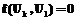 в следующих двух случаях: если дуги
в следующих двух случаях: если дуги 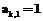 определяют связи между дугами, которые могут быть основными и дополнительными. Основные связи определяют непосредственное предшествование дуг, когда конец одной дуги
определяют связи между дугами, которые могут быть основными и дополнительными. Основные связи определяют непосредственное предшествование дуг, когда конец одной дуги 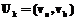 совпадает с началом другой
совпадает с началом другой 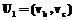 . Матрицу следования дуг, в которой есть основные и все дополнительные связи, будем называть полной матрицей следования дуг, а если в ней не все дополнительные связи – неполной матрицей следования дуг. Имея матрицу смежности дуг или неполную матрицу следования дуг, можно получить полную матрицу следования дуг, если учесть, что отношение частичного порядка транзитивно: если
. Матрицу следования дуг, в которой есть основные и все дополнительные связи, будем называть полной матрицей следования дуг, а если в ней не все дополнительные связи – неполной матрицей следования дуг. Имея матрицу смежности дуг или неполную матрицу следования дуг, можно получить полную матрицу следования дуг, если учесть, что отношение частичного порядка транзитивно: если 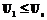 , то
, то 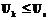 .
.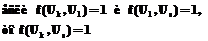 . (2)
. (2)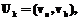
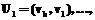
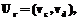
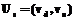 . Тогда подматрица полной матрицы следования дуг, образованная пересечением строк и столбцов дуг, образующих цикл, состоит из единиц.
. Тогда подматрица полной матрицы следования дуг, образованная пересечением строк и столбцов дуг, образующих цикл, состоит из единиц.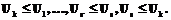 Поскольку отношение частичного порядка транзитивно, то имеет место:
Поскольку отношение частичного порядка транзитивно, то имеет место: 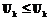 ,
, 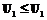 ,
, 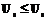 ,
, 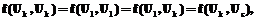 то есть
то есть 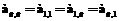 , что и требовалось доказать.
, что и требовалось доказать.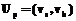 имеем
имеем  .
.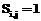 , то
, то 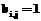 , где
, где 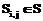 ,
, 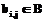 и В=А(А+Е).
и В=А(А+Е).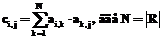 .
. , тогда и только тогда, когда
, тогда и только тогда, когда 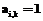 и
и 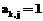 , то есть тогда и только тогда, когда дуга Uk следует за другой Ui и дуга Uk предшествует дуге Uj. Следовательно, численное значение
, то есть тогда и только тогда, когда дуга Uk следует за другой Ui и дуга Uk предшествует дуге Uj. Следовательно, численное значение 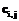 будет равно числу дуг, заключенных между дугами Ui и Uj.
будет равно числу дуг, заключенных между дугами Ui и Uj.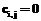 будут в следующих случаях:
будут в следующих случаях: предшествует дуге
предшествует дуге 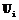 , то есть
, то есть  ;
;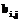 вычисляются по формуле:
вычисляются по формуле: 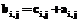 .
.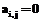 , то есть дуги
, то есть дуги 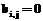 , так как
, так как 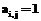 , то
, то 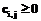 , причем
, причем 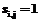 , то и
, то и 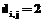 , где
, где  и
и 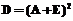 .
.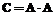 удовлетворяют соотношению:
удовлетворяют соотношению: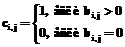 ,
,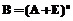 ,
, 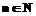 , то матрица D=С–Е также является матрицей следования дуг.
, то матрица D=С–Е также является матрицей следования дуг.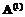 и
и 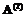 – матрицы следования ориентированного ациклического графа [G,£] при одинаковом упорядочении дуг, Е – единичная матрица. Определим матрицу
– матрицы следования ориентированного ациклического графа [G,£] при одинаковом упорядочении дуг, Е – единичная матрица. Определим матрицу 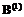 в виде
в виде 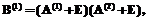 а элементы
а элементы 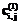 матрицы
матрицы 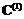

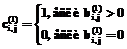 .
.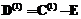 также является матрицей следования дуг.
также является матрицей следования дуг.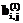 матрицы B
матрицы B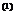 вычисляются по формуле:
вычисляются по формуле: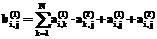 , (3)
, (3)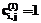 , если
, если 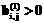 , а так как матрицы
, а так как матрицы 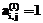 и (или)
и (или) 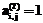 , то
, то 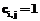 . Если
. Если 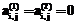 , то
, то 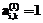 и
и 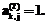 Учитывая, что
Учитывая, что 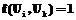 и
и 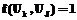 , то есть если
, то есть если 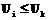 и
и 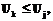 следовательно,
следовательно, 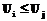 .
.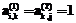 , иначе
, иначе 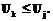
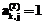 , то получаем
, то получаем 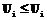 , то есть граф [G,≤] имеет цикл, что противоречит условиям леммы. Поскольку диагональные элементы
, то есть граф [G,≤] имеет цикл, что противоречит условиям леммы. Поскольку диагональные элементы 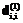 матрицы
матрицы 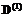 равны нулю, то матрица
равны нулю, то матрица 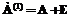 и
и 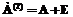 , из леммы 2 следует, что D – матрица следования дуг. Пусть утверждение верно при p=n–1. Обозначив
, из леммы 2 следует, что D – матрица следования дуг. Пусть утверждение верно при p=n–1. Обозначив  и А+Е=А(2) и воспользовавшись леммой 2, получим, что утверждение теоремы верно при любом n.
и А+Е=А(2) и воспользовавшись леммой 2, получим, что утверждение теоремы верно при любом n.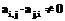 ,
, 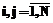 , то переходим к п. 11 (контроль исходных данных).
, то переходим к п. 11 (контроль исходных данных).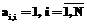 (получение матрицы А+Е).
(получение матрицы А+Е).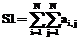 .
.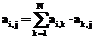 .
.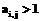 , то присваиваем
, то присваиваем  .
.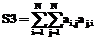 . Если S3>N (контроль на наличие циклов), то переходим к п. 11.
. Если S3>N (контроль на наличие циклов), то переходим к п. 11.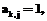 вычисляем
вычисляем 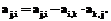
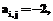 то
то 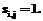
 Исходными данными служат список работ проекта и экспертная оценка связей между работами, которая определяется в диалоговом режиме.
Исходными данными служат список работ проекта и экспертная оценка связей между работами, которая определяется в диалоговом режиме.