Авторитетность издания
Добавить в закладки
Следующий номер на сайте
О совмещении спектральных и временных оценок
Аннотация:
Abstract:
| Автор: Юшин В.И. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 16781 |
Версия для печати Выпуск в формате PDF (1.17Мб) |
Спектральные представления анализируемых сигналов в настоящее время столь же привычны, как и их осциллографическое изучение. Однако традиционные оценки в виде спектральной плотности мощности (СПМ) или амплитудных спектров страдают тем существенным недостатком, что по ним трудно проводить абсолютные количественные сопоставления сигналов разных типов или сравнивать параметры сигналов во временной и частотной области. Причина не только в том, что временные и спектральные представления имеют разные физические размерности. Даже оценки одной природы, как, например, СПМ и просто амплитудный спектр, точнее, спектральная плотность амплитуд, количественно на одном графике и в одном масштабе несопоставимы. В конечном итоге это сужает практическое применение спектров, зачастую ограничивая их арсенал нормированными оценками. В настоящей статье сделана попытка анализа некоторых спектральных оценок, позволяющих более целенаправленно анализировать колебания любого характера, а также использующихся для тестирования аппаратурного тракта по собственным шумам. Обращение к этой проблеме вызвано тем, что с внедрением цифровых осциллографов, регистраторов и мощных персональных компьютеров алгоритмы спектральных преобразований стали легко доступными практикам. Однако пользуются ими не всегда корректно. Предлагаемые ниже оценки представляют собой функциональные преобразования от традиционных спектральных оценок, таких как амплитудный спектр, периодограмма, спектральная плотность мощности [1,2], и ни в коей мере не затрагивают классические основы спектрального анализа. Более того, некоторые из них встречаются и в классической теории, но, к сожалению, еще не получили достойного применения на практике. Спектр, периодограмма и спектральная плотность мощности Пусть функция времени Понятие и определение комплексного спектра Фурье может относиться к любому физически возможному сигналу
Комплексный спектр Фурье (1) определен на всей частотной оси и имеет размерность код·с, или код/Гц. Обозначим его модуль как
где
называется в теории случайных функций [1,2] периодограммой, а точнее, односторонней периодограммой. Если
где M – символ операции математического ожидания – усреднения по ансамблю реализаций. Как видим, для получения СПМ через амплитудный спектр необходимы два предельных перехода – по времени и по множеству. При этом, как доказал В.С. Пугачев [3], операция M не может быть заменена предельным переходом при Т → ∞ (удлинением интервала Фурье-преобразования). Это связано с тем обстоятельством, что оценка периодограммы по одной, даже сколь угодно длинной реализации В результате ее график выглядит как очень сильно и беспорядочно осциллирующая в неотрицательной области функция, причем с ростом интервала Т размах осцилляций не убывает, а становится лишь более "высокочастотным". Такую функцию можно сгладить, применив простое усреднение в скользящем окне вдоль частотной оси, что часто используется на практике. В [3] показано, что для случайного процесса это как раз и эквивалентно тому, что исходная длинная реализация разбивается на ряд более коротких отрезков, после чего оценка спектральной плотности все равно находится по множеству периодограмм этих отрезков в соответствии с выражением (4). В целом корректная оценка СПМ эргодического стационарного случайного процесса может быть получена тремя статистически равноценными способами. Первый способ, как упомянуто, состоит в разбиении длинной реализации x(t) на множество К относительно коротких (длиной Т каждый) отрезков, в вычислении по каждому из них периодограммы (3) и с последующим их усреднением по полученному множеству К:
Второй способ состоит в однократном вычислении периодограммы (3) и последующим сглаживанием ее вдоль оси частот. Третий способ следует из альтернативного определения СПМ как преобразования Фурье автокорреляционной функ ции (здесь мы на нем не будем останавливаться). На практике, однако, вместо СПМ чаще всего используют недостаточно усредненную или даже одиночную периодограмму (3) со всеми ее недостатками. Помимо сильной изрезанности, которая мешает, например, поместить на один график несколько сравниваемых спектров, периодограмма (и СПМ) имеет еще два существенных с точки зрения визуального анализа недостатка. Если в анализируемом сигнале присутствуют гармонические компоненты, то они проявляются в виде узких спектральных линий большой амплитуды, совершенно неадекватной их сравнительному с шумовой компонентой уровню в исходном сигнале. Их амплитуда пропорциональна интервалу Т, тогда как уровень сплошной части СПМ не зависит от Т. Другой недостаток состоит в следующем. СПМ (как и периодограмма) имеет размерность код2 с или код2/Гц и физически может интерпретироваться как средняя мощность (или дисперсия) исходного сигнала в фиксированной абсолютной полосе частот шириной 1 Гц в окрестности данной частоты. Однако на графике функции времени (например сейсмограмме) человек способен визуально охватить лишь ограниченную относительную полосу частот независимо от того, к какой области абсолютных частот относится эта запись. В результате восприятие спектральной плотности оказывается в целом искажено относительно субъективного восприятия исходного сигнала неадекватным подчеркиванием низкочастотных составляющих. С другой стороны, привычным способом частотного анализа во временной области является полосовая или узкополосная фильтрация. Она сохраняет временное представление сигнала, в то же время снабжая его спектральными параметрами, такими как центральная частота и полоса частот. Чтобы сопоставить наблюдаемые амплитуды и мощность такого отфильтрованного сигнала с его СПМ, заданной в широкой полосе частот, необходимо выполнить интегрирование последней в соответствующей узкой полосе. Но если эту операцию приходится (явно или мысленно) выполнять почти всегда, то возникает вопрос, не проще ли заранее преобразовать спектральную плотность таким образом, чтобы результат был бы сразу сопоставим с привычными амплитудными оценками сигнала? Непосредственно же к СПМ целесообразно обращаться лишь тогда, когда это действительно необходимо, например, для вычисления корреляционных функций, расчета оптимальных операторов и т.п. Октавные спектры. Рассмотрим скользящее интегральное преобразование односторонней спектральной плотности в области положительных частот вида
где a – постоянный коэффициент, определяющий относительную ширину полосы частот, в которой выполняется интегрирование односторонней спектральной плотности, то есть, вычисляется дисперсия отфильтрованного сигнала. Полагая, что на коротком интервале интегрирования по частоте спектральная плотность случайного сигнала изменяется мало, можем приближенно вместо (6) записать:
Величина a выражается через основание относительной шкалы частот
На практике используются полосы: треть октавы (a –1 = 0.26), 1/6 октавы (a –1 = 0.12) и примерно равная ей величина 1/20 декады (a –1 = 0.12). Соответствующие октавные спектры выразим как: Поскольку мы в действительности не выполняли интегрирование (6), а дали оценку ожидаемой величине того или иного октавного спектра исключительно по "мгновенным" значениям исходной СПМ, то в качестве общего определения октавного спектра дисперсии примем самое простое выражение (8). Оно показывает, какова была бы средняя мощность данного случайного сигнала в полосе частот в одну октаву, если бы спектральная плотность этого сигнала была бы постоянна в этой полосе и равна ее фактическому значению на данной абсолютной частоте f. Тем самым мы переводим размерность СПМ в привычную физически ощутимую размерность мощности сигнала – код2. Переход от октавы к другой относительной полосе частот сводится, как показано выше, всего лишь к умножению октавного спектра на соответствующий коэффициент. Определим также спектр октавного среднеквадратического отклонения (СКО) как
Спектры гармоник. С точки зрения наглядности спектрального анализа сложных сигналов, содержащих как случайный шум, так и гармонические компоненты, СПМ и октавные спектры в определении (8) неудовлетворительны. Строго говоря, указанные характеристики адекватны только для чисто случайных сигналов. Если же в исходном сигнале присутствуют стабильные гармонические компоненты, которые обнаруживаются в виде спектральных линий на амплитудных спектрах и периодограммах, то оценивать их амплитуды по периодограммам, СПМ или октавным спектрам без дополнительной информации нельзя. Спектральное преобразование надо видоизменить. Разумно потребовать, чтобы амплитуды спектральных линий в такой спектральной оценке совпадали бы по размерности и величине с амплитудами или мощностями гармонических составляющих независимо от длины анализируемой реализации Т. При этом придется пожертвовать правильным отображением сплошной части спектра. Этому требованию отвечает простое масштабирование обычного амплитудного спектра (2), полученного по одной реализации, коэффициентом, обратным ее длительности Т:
Выражение (10) назовем спектром амплитуд гармоник, или спектром гармоник. Оно имеет ту же размерность, что и исходный сигнал. Используя это выражение, можно по амплитудному спектру (2) измерить абсолютные амплитуды и частоты всех стабильных по частоте гармонических компонент в исходном сигнале, даже если они лежат ниже уровня шума. Здесь Фурье-преобразование выступает как оператор оптимального выделения монохроматических колебаний на фоне шума. Сравнивать затем полученные амплитуды гармоник следует с суммарным среднеквадратическим уровнем исходного сигнала, вычисленного во временной области, или же со сплошной частью октавного спектра СКО (9). Для этого достаточно просто поместить на общий график обе спектральные оценки и принимать во внимание в октавном спектре только сплошную часть, игнорируя его непомерно большие спектральные линии, а в спектре гармоник – только эти линии. В некоторых случаях вместо спектра амплитуд гармоник удобнее пользоваться спектром мощностей гармоник, который определяется как
имеет размерность мощности сигнала и может сравниваться непосредственно со сплошной частью октавного спектра дисперсии (8). Отметим, однако, принципиальное отличие оценок СПМ и спектра гармоник. Если первая является статистической характеристикой и для получения ее состоятельной оценки требуется усреднение множества периодограмм по достаточно большой выборке или частотное сглаживание, то вторая представляет собой оценку параметра амплитуды детерминированного сигнала, замаскированного случайным шумом; здесь требуется выборка, лишь минимально необходимая для того, чтобы детерминированная гармоническая компонента проявилась как спектральная линия. Требование минимизации длины анализируемой реализации становится актуальным, если частота гармоники нестабильна. В этом случае спектральная линия размывается (расширяется и падает по амплитуде), и, стало быть, спектр гармоник становится недостоверным. Критерий корректности оценки спектра амплитуд гармоник – наблюдаемая ширина спектральной линии, которая, как известно, должна быть обратной длине Т исходной реализации сигнала. Но и "правильная" ширина спектральной линии не гарантирует точности ее измерения. Известно, что при использовании БПФ для анализа сигналов, содержащих гармоники, некратные по периоду интервалу анализа, без существенного увеличения исходного временного массива за счет дополнительных нулей, имеет место «эффект растекания», природа которого сродни алайсинг-эффекту. В результате наблюдаемые амплитуды спектральных линий могут оказаться ниже истинных значений в худшем случае на 30%. Этому недостатку подвержен и спектр гармоник. Всех перечисленных недостатков лишена следующая, наиболее универсальная спектральная оценка – интегральный спектр, или спектральная функция [1,2]. Интегральные спектры дисперсии и среднеквадратического отклонения Интегральный спектр дисперсии определяется как дисперсия сигнала в переменной полосе частот, начиная от некоторой фиксированной f0 до текущей частоты f. Он вычисляется интегрированием СПМ или периодограммы в переменной полосе частот с фиксированным нижним пределом:
Частота f0 здесь выступает как параметр, а f как аргумент интегрального спектра. Соответственно, можно определить интегральный спектр СКО как Для получения интегрального спектра можно использовать вместо спектральной плотности S(f) даже одиночную периодограмму ST(f), что делает интегральный спектр универсальным инструментом анализа шумоподобных и гармонических сигналов, включая нестабильные по частоте и свип-сигналы. Выбор начальной частоты интегрирования f0 определяется характером решаемой задачи, но во всех случаях она не должна быть ниже, чем 1/Т, где Т – длина реализации, по которой вычисляется периодограмма. Важнейшие свойства интегральных спектров достаточно очевидны, исходя из определения (12) и положительной определенности СПМ. 1. Интегральный спектр является неубывающей функцией частоты. 2. Дисперсия сигнала в любой заданной фиксированной полосе частот
3. Конечное значение интегрального спектра дисперсии равно общей дисперсии сигнала, вычисленной непосредственно во временной области, а интегрального спектра СКО, соответственно, СКО сигнала. Это свойство, в частности, удобно использовать для контроля правильности вычисления интегральных спектров.
С точки зрения практического спектрального анализа это достоинство очень существенно, поскольку позволяет наносить на один график несколько однотипных спектров разных сигналов, не сливающихся в неразборчивую картину. 5. Наличие гармонической составляющей в сигнале проявляется в интегральном спектре дисперсии в виде скачка, высота которого равна мощности гармоники. Если гармоника нестабильна по частоте, это приводит лишь к сглаживанию фронта такого скачка, но высота его все равно сохраняется равной мощности гармоники. Важно особо подчеркнуть это достоинство интегрального спектра, которое делает его нечувствительным также и к вышеупомянутому "эффекту растекания". Благодаря этому свойству при формировании массива для БПФ нет необходимости увеличивать его за счет дополнительных нулей, что приходится делать, например, при вычислении спектра гармоник, чтобы избежать "растекания". 6. Оценки интегральных спектров независимо от типа сигналов инвариантны к длине реализации. Это означает, в частности, что если программа БПФ не имеет ограничений по максимальной длине массива, вычисление интегрального спектра целесообразно выполнять по одной периодограмме без разбиения реализации на псевдоансамбль. Если же такие ограничения существуют, то при создании псевдоансамбля из одной длинной реализации не имеет значения, на сколько отрезков ее резать и какой длины они должны быть. 7. Интегральные спектры дисперсии обладают свойством аддитивности по отношению к любым непрерывным квазистационарным процессам, таким как шумоподобные, гармонические, частотно-модулированные и т.п. Другими словами, смесь стационарного шума и квазигармонических колебаний имеет интегральный спектр дисперсии, равный сумме интегральных спектров составляющих. Таким образом, интегральный спектр мощности является наиболее универсальной из наглядных спектральных оценок для анализа непрерывных колебаний различной природы. Чтобы привыкнуть правильно интерпретировать его, полезно промоделировать это преобразование на тест-сигналах разного типа. На рисунке 1 показан синтетический сигнал и его интегральный спектр мощности. Тест-сигнал (рис. 1а) состоит из случайного шума, трех гармонических компонент и свип-сигнала – все одинаковой мощности. Частоты гармонических компонент равны 30, 55 и 72 Гц, свип на интервале анализа пробегает полосу частот 50–100 Гц. На рис.1б показаны интегральные спектры мощности каждой из этих компонент и суммарного сигнала. Важно еще раз отметить: спектр суммарного сигнала равен сумме интегральных спектров мощности всех его компонент, что хорошо видно по графику. Высота скачков в интегральном спектре равна точно мощностям гармоник. Средняя мощность свип-сигнала определяется по перепаду значений интегрального спектра этой компоненты на его конечной и начальной частоте. Полоса частот шума шире полосы частот графика, и поэтому его спектральная функция продолжает монотонно возрастать на всем частотном интервале.
На рисунке 2а показан короткий фрагмент записи колебаний, полученной на удалении 50 км от мощного сейсмического вибратора. Вибратор работал на постоянной частоте 8 Гц. Для спектрального анализа был взят отрезок продолжительностью 40 с при частоте дискретизации 100 Гц. На рисунке 2б показаны несглаженная и сглаженная по частоте скользящим окном по 10 соседним ординатам периодограмма в логарифмическом масштабе по ординате, поскольку в линейном масштабе первая просто необозрима. На рисунке 2в на одном графике представлены октавный спектр СКО, полученный по сглаженной периодограмме, и спектр амплитуд гармоник. Здесь уже можно сопоставлять СКО случайной составляющей в октавной полосе частот и амплитуду наблюдаемых спектральных линий в спектре гармоник. Все они имеют размерность первичного сигнала код. На рисунке 2г показан интегральный спектр мощности этого сигнала в линейном (что важно!) масштабе. Величина крутого большого скачка точно соответствует мощности гармонического сигнала вибратора. Другие уступы в этой кривой также отображают мощности каких-то сторонних гармонических помех. Максимальное значение равно дисперсии исходного сигнала, в чем мы убедились непосредственно по первичному сигналу. Список литературы 1. Дженкинс Г., Ваттс Д. Спектральный анализ и его приложения. - М.: Мир. - Т. 1. - 1971. 2. Бендат Дж., Пирсол А. Измерение и анализ случайных процессов. - М.: Мир, 1974. 3. Пугачев В.С. Теория случайных функций и ее применение к задачам автоматического управления. - М.: Физматгиз, 3-е изд., 1962. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=555 |
Версия для печати Выпуск в формате PDF (1.17Мб) |
| Статья опубликована в выпуске журнала № 1 за 2005 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Компьютерная технология проектирования перестраиваемых нерекурсивных фильтров
- Расчет нечеткого сбалансированного показателя в задачах взвешивания терминов электронных документов
- Новый подход к проблеме коллективного выбора на базе удовлетворения взаимных требований сторон
- Прототип интеллектуальной системы поддержки принятия решений для управления энергообъектом
- Сравнение сложных программных систем по критерию функциональной полноты
Назад, к списку статей



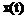 представляет собой цифровую запись некоторого физического процесса, то есть безразмерное число. Чтобы оттенить этот факт, будем обозначать такую "безразмерную размерность" единицей код (в зависимости от конкретной задачи ее затем можно заменить любой физической величиной).
представляет собой цифровую запись некоторого физического процесса, то есть безразмерное число. Чтобы оттенить этот факт, будем обозначать такую "безразмерную размерность" единицей код (в зависимости от конкретной задачи ее затем можно заменить любой физической величиной).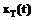 ограниченной продолжительности T или к произвольно выбранному отрезку [0,T] не ограниченного во времени сигнала x(t):
ограниченной продолжительности T или к произвольно выбранному отрезку [0,T] не ограниченного во времени сигнала x(t): . (1)
. (1) , (2)
, (2)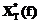 – комплексно сопряженный спектр. Функцию
– комплексно сопряженный спектр. Функцию  обычно называют амплитудным спектром, а точнее, спектральной плотностью амплитуд. Здесь индекс Т напоминает об ее зависимости от интервала времени, на котором выполнялось преобразование. Функция от комплексного спектра (1), определенная только на положительных частотах, вида
обычно называют амплитудным спектром, а точнее, спектральной плотностью амплитуд. Здесь индекс Т напоминает об ее зависимости от интервала времени, на котором выполнялось преобразование. Функция от комплексного спектра (1), определенная только на положительных частотах, вида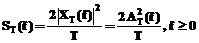 (3)
(3)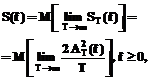 (4)
(4)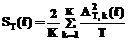 . (5)
. (5)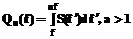 , (6)
, (6) . (7)
. (7) (обычно это октава,
(обычно это октава,  . При полосе ровно в одну октаву a–1=1 и выражение (7) получается простейшим:
. При полосе ровно в одну октаву a–1=1 и выражение (7) получается простейшим: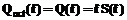 . (8)
. (8)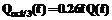 ,
,  и т.п. Как видим, все они различаются только безразмерным масштабным коэффициентом.
и т.п. Как видим, все они различаются только безразмерным масштабным коэффициентом. . (9)
. (9) . (10)
. (10)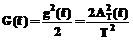 , (11)
, (11)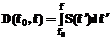 . (12)
. (12)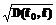 , но эта оценка менее удобна.
, но эта оценка менее удобна.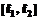 определяется просто как разность значений интегрального спектра дисперсии на этих граничных частотах:
определяется просто как разность значений интегрального спектра дисперсии на этих граничных частотах: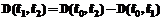 . (13)
. (13)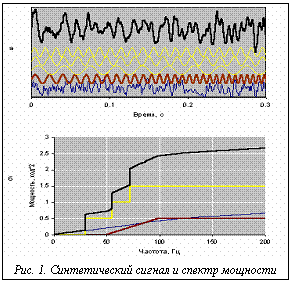 4. Крутизна возрастания интегрального спектра пропорциональна СПМ. Мы намеренно употребляем здесь понятие крутизна вместо производная, поскольку, во-первых, производная не всегда существует, а во-вторых, когда оценка интегрального спектра определяется по одиночной периодограмме, его производная (то есть сама периодограмма) является сильно осциллирующей, визуально нечитаемой функцией, тогда как интегральный спектр выглядит всего лишь как шероховатая, но вполне локализованная кривая, имеющая хорошо различимую глазом крутизну.
4. Крутизна возрастания интегрального спектра пропорциональна СПМ. Мы намеренно употребляем здесь понятие крутизна вместо производная, поскольку, во-первых, производная не всегда существует, а во-вторых, когда оценка интегрального спектра определяется по одиночной периодограмме, его производная (то есть сама периодограмма) является сильно осциллирующей, визуально нечитаемой функцией, тогда как интегральный спектр выглядит всего лишь как шероховатая, но вполне локализованная кривая, имеющая хорошо различимую глазом крутизну.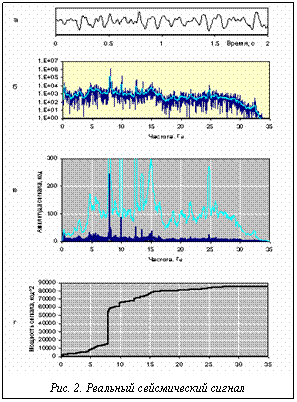 На рисунке 2 проиллюстрированы спектральные оценки при анализе реального сейсмического сигнала, содержащего шум и гармоническую составляющую.
На рисунке 2 проиллюстрированы спектральные оценки при анализе реального сейсмического сигнала, содержащего шум и гармоническую составляющую.