Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Authors: () - , () - , () - , () - | |
| Ключевое слово: |
|
| Page views: 10276 |
Print version Full issue in PDF (1.17Mb) |
Рассмотрим систему с жестким циклом реального времени (РВ) Δτ, обрабатывающую информацию, снимаемую со множества однородных источников данных {Di}, i=1,2,…,M. Данные от источников могут обрабатываться с помощью N типов задач {Zj}, причем решение задачи Zj автоматически включает в себя решение задачи Zj+1, j=1,2,…,N-1, над подмножеством того же набора данных. Решаемая на цикле РВ задача Zj может обрабатывать подмножество данных Dij только от одного источника i: Di,1= Di; Di,j+1 На цикле РВ может быть решено Kj экземпляров задачи Zj, каждый со своим набором данных. Будем считать, что все Kj являются делителя- ми М. Информация на любом источнике данных может возникать случайно независимо друг от друга, причем момент времени ее возникновения не может быть сообщен системе обработки. Степень полноты j данных источника i описывается множеством вероятностей {Pj}, j=1,2,…,N.
Время актуальности данных типа j источников Δtj ограничено и имеет функцию распределения вероятностей Gj(t)=P{Δtj Для решения задачи Zj система потребляет Rlj количество ресурса l, общая составляющая которого ограничена величиной Rlmax, l=1,2,…,L. Причем Для описанной системы требуется построить расписание решения задач Zj над данными Di для обеспечения минимальной вероятности потери данных при существовании ограничений на потребляемые ресурсы системы. Рассмотрим множество алгоритмов А(F), где F = {F0, F1, …, FN} – вектор частот запуска на решение задач Zj каждого типа; F0 – число циклов РВ, на которых не решаются никакие задачи; Fj – количество запусков задач j-го типа, необходимое для обработки всего множества данных. Любой из алгоритмов А(F) является периодическим; период в циклах РВ равен
На периоде работы алгоритма задача типа j решается
Рассмотрим только те алгоритмы из множества А(F), которые имеют наименьшую сумму дисперсий случайных величин τj, оставив за рамками данной статьи способы их построения. В этом случае можно считать, что попытки обработки конкретного набора данных типа j в пределах периода работы алгоритма также являются периодическими процессами с периодом, заданным выражением (3). Так как данные на источниках информации могут появляться равновероятно на периоде их обработок, то вероятность потери данных для источника типа j будет равна
а общая вероятность потери данных
Оценим ресурсы, потребляемые А(F):
На основе полученных выражений (4) и (5) теперь можно дать формальную постановку решаемой задачи, а именно: найти целочисленные значения координат вектора F = {F0, F1, …, FN}, минимизирующие (5), при ограничениях
В общем случае сформулированная задача представляет собой задачу нелинейной целочисленной оптимизации. Причем ее решение не ограничено сверху в том смысле, что если вектор F есть решение, то вектор αF также является решением для всех целых значений α ≥ 2. Поэтому целесообразно ввести дополнительный критерий
В ряде случаев для рассматриваемой задачи диспетчирования достаточно задать наибольшее допустимое значение вероятности потерь Qmax. В этом случае критерий (8) становится основным, а к ограничениям (7) добавляется ограничение
Покажем, что в этой постановке задача может быть сведена к линейной целочисленной задаче. Из выражений (1) и (5) следует, что достаточным условием выполнения ограничения (9) является выполнение системы неравенств Qj ≤ Qmax для всех j. Рассмотрим следующие функции
Для них справедливо при любых распределениях Gj(t): 1. 2. 3. Таким образом, для заданного ограничения Qmax>0 для всех j мы можем найти τj пор=φ1j(Qmax). Причем при ограничение (9) автоматически удовлетворяется, а, как видно из (2) и (3), ограничение (10) преобразуется к линейному относительно F. Последовательные алгоритмы диспетчирования не учитывают в полной мере вероятностные распределения моментов возникновения и периодов актуальности обрабатываемых данных. Такой учет возможен только тогда, когда управление запуском задач на обработку осуществляется индивидуально по каждому источнику. Пусть известна матрица вероятностей возникновения j-го типа данных на i-м источнике
Зададим матрицы W – текущих весов, ΔW – статических весов и T – счетчиков неопрошенных циклов размерности N×M и матрицу-строку из L элементов ΔR – среднее (на цикл РВ) потребление ресурсов. Элементы матрицы ΔW заполним из следующих посылок: 1) чем больше вероятность pji, тем больше элемент Δwji; 2) чем больше математическое ожидание времени актуальности данных, тем меньше элемент Δwji.
Первоначально заполним матрицу W=ΔW, ΔR=0 и T=0. Вес запускаемой задачи типа j, обрабатывающей данные от i-го источника, определим как Представим алгоритм запуска задач в следующем виде. 1. Найдем минимальный тип задачи jmin, удовлетворяющий ограничениям на ресурсы, исходя из текущего состояния ΔR и ресурсов, потребляемых Kj экземплярами задачи Zj. Если никакой тип задачи не может быть запущен, то цикл РВ пропускаем. Переходим к п. 3, иначе – к п. 2. 2. Для всех уровней задач j ≥ jmin множество Ij формируется из Kj элементов – источников данных, для которых 3. В соответствии с выбранным типом задач пересчитываем матрицу ΔR. Для матриц W и T все элементы j* строки и столбцов с индексами из множества Ij* обнуляются. К остальным элементам матрицы W прибавляются соответствующие элементы матрицы ΔW, а к остальным элементам матрицы T прибавляется 1. Переходим к новому циклу РВ (п. 1). Адаптивный алгоритм динамического построения расписания запуска задач был исследован на имитационной модели системы. Результаты проведенных исследований показали, что матрица статических весов, задаваемая (11), не является оптимальной в том смысле, что не обеспечивает при работе алгоритма наименьшую вероятность потери данных. На основе выражения (10) был построен алгоритм получения весовой матрицы ΔW, а на имитационной модели получены более высокие показатели эффективности алгоритма. Задача построения статического последовательного алгоритма диспетчирования сведена к целочисленной задаче линейного программирования, решение которой позволяет получить параметры алгоритма, обеспечивающие заданную вероятность потери данных. Построен адаптивный динамический алгоритм, который при оптимизации его параметров обеспечивает более высокие показатели эффективности. |
| Permanent link: http://swsys.ru/index.php?page=article&id=548&lang=&lang=en |
Print version Full issue in PDF (1.17Mb) |
| The article was published in issue no. № 1, 2005 |
Perhaps, you might be interested in the following articles of similar topics:
- Информационно-вычислительный комплекс по применению мембран в биотехнологии
- Программные средства автоматизации приборостроительного производства изделий радиоэлектронной аппаратуры
- Интеллектуальные хранилища данных в системах государственного управления
- ДИНАМИКА-2 - программа для решения осесимметричных и плоских задач
- Общедоступные математические САПР для персональных компьютеров класса IBM PC
Back to the list of articles
 Dij.
Dij. (1)
(1) .
.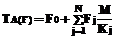 . (2)
. (2)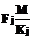 раз, а средний интервал времени между последовательными попытками обработки конкретного набора данных типа j одной из задач типа n (n ≤ j) будет равен
раз, а средний интервал времени между последовательными попытками обработки конкретного набора данных типа j одной из задач типа n (n ≤ j) будет равен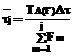 . (3)
. (3) , (4)
, (4) . (5)
. (5)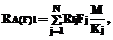 l = 1, 2, … , L. (6)
l = 1, 2, … , L. (6) . (7)
. (7)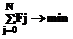 . (8)
. (8)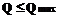 . (9)
. (9) .
.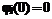 ,
, ,
,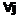 , если
, если 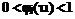 и τ2 > τ1, то
и τ2 > τ1, то 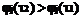 .
.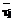 ≤ τj пор (10)
≤ τj пор (10)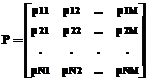 .
. . (11)
. (11) . (12)
. (12)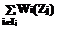 (12) максимальна. Среди максимальных элементов для каждого уровня найдем максимальный. Если таких элементов несколько, то выбирается тот, у которого по матрице T наибольшая сумма неопрошенных циклов. Пусть уровень этого элемента равен j*. Тогда на данном цикле РВ запускается
(12) максимальна. Среди максимальных элементов для каждого уровня найдем максимальный. Если таких элементов несколько, то выбирается тот, у которого по матрице T наибольшая сумма неопрошенных циклов. Пусть уровень этого элемента равен j*. Тогда на данном цикле РВ запускается 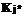 экземпляров задачи
экземпляров задачи  над источниками данных из множества
над источниками данных из множества  . Переходим к пункту 3.
. Переходим к пункту 3.