Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Исследование компьютерных методов построения моделей сложных объектов
Аннотация:
Abstract:
| Авторы: Усков А.А. (prof.uskov@gmail.com) - Российский университет кооперации, г. Мытищи, Россия, доктор технических наук, Санатин Д.В. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 13439 |
Версия для печати Выпуск в формате PDF (1.97Мб) |
Методы идентификации сложных объектов имеют важное значение при создании систем поддержки принятия управленческих решений, используемых в самых различных предметных областях. Большинство методов, используемых при решении задач идентификации, включают в себя алгоритмы построения моделей статических объектов, которые во многом и определяют эффективность данных методов. К числу наиболее известных методов идентификации статических объектов можно отнести: модели, основанные на методе наименьших квадратов (МНК); непараметрические (локально-аппроксимационные) и нейросетевые модели. В настоящей статье приводятся результаты экспериментального исследования указанных методов, касающиеся точности получаемых моделей, а также вычислительных затрат, требуемых для их построения и тестирования. Пусть имеется статический объект, имеющий n входов (векторный вход y = η( где η( Необходимо построить модели данного статического объекта (оценки функций η( < с использованием различных методов и определить затраты машинного времени на создание и тестирование моделей. Экспериментальное исследование методов идентификации статических объектов при решении поставленной задачи предполагает построение моделей множества самых различных объектов, описываемых формулой (1), с использованием различных алгоритмов и сравнение свойств полученных моделей. В связи с ограниченным объемом статьи приведем результаты построения и исследования свойств моделей одного объекта, имеющего ярко выраженный нелинейный характер при нормальном законе распределения аддитивной помехи ξ, описываемым формулой (1), при
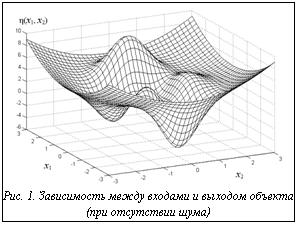
Вид зависимости (3) на области определения входных сигналов объекта представлен на рисун- ке 1. В качестве алгоритмов построения моделей объекта были использованы следующие: 1) метод аппроксимации искомой зависимости полиномом k-го порядка, определение коэффициентов полинома осуществляется по методу наименьших квадратов (Pk) [1] (получаемые с использованием данного метода модели аналогичны моделям на основе нейронных Σ-Π сетей [2]); 2) локальная аппроксимация с линейными локальными функциями и числом ближайших узлов для нахождения параметров функции, равным M (метод M ближайших узлов – LA M) [3]; 3) нейронная сеть с радиальными базисными функциями, имеющая линейный выходной слой (RBFN) [2], для построения которой используется алгоритм самоорганизации, решающий задачу максимизации точности модели, при минималь 4) 5) нейронная сеть, многослойный персептрон (MLP) [2], содержащая два скрытых слоя, состоящих из 12 и 5 нейронов соответственно с сигмоидальными функциями активации, метод обучения – один из видов квазиньютоновского алгоритма обратного распространения ошибки, реализованный в системе MATLAB [4]. Для построения моделей количество обучающих точек N (см. (2)) было выбрано равным 64. При этом было рассмотрено два случая расположения обучающих точек: в узлах равномерной сетки и случайное с равномерным законом распределения. Для вычисления среднеквадратической ошибки моделей количество тестирующих точек было выбрано равным 400 (тестирующие точки располагались в узлах равномерной сетки и не совпадали с обучающими). Полученные зависимости среднеквадратической ошибки (E) моделей рассматриваемого объекта от уровня среднеквадратического отклонения (СКО) (σ) случайной составляющей ξ представлены на рисунках 2 и 3. Приведем вычислительные затраты, определяемые как требуемое машинное время, выраженное в относительных единицах на получение аппроксимационных моделей, и их тестирование для рассматриваемого примера (рис. 4).
Можно выделить следующие особенности исследованных методов идентификации. 1. Полиномиальные МНК модели имеют низкую точность при существенном отличии аппроксимируемой зависимости от полиномиальной, в то же время малочувствительны к аддитивной помехе. Вычислительные затраты на построение и тестирование данных моделей относительно малы. 2. Локально-аппроксимационные модели (метод M ближайших узлов) с линейными локальными функциями имеют достаточно высокую точность, однако очень чувствительны к наличию аддитивного шума. Следует заметить, что с ростом M увеличивается погрешность получаемых моделей и уменьшается чувствительность к шуму. Вычислительные затраты при построении модели весьма незначительны. В то же время при тестировании поиск отклика модели занимает относительно длительное время. 3. Модели на основе сетей с радиальными базисными функциями, имеющих линейный выходной слой (RBFN), показали относительно высокую точность, невысокую чувствительность к аддитивному шуму и невысокие вычислительные затраты. 4. Модели на основе обобщенно-регрессионных нейронных сетей (GRNN) – разновидность нейронной сети с радиальными базисными функциями – имеют достаточно высокую точность и относительно невысокую чувствительность к аддитивному шуму, особенно это проявляется при случайном расположении обучающих точек. Вычислительные затраты на построение и тестирование указанных моделей достаточно малы. Однако, в отличие от моделей, построенных на основе RBFN, с ростом обучающей выборки в данном случае могут возникнуть вычислительные сложности. 5. Модели на основе многослойных персептронов (MLP) показали средние результаты по точности и высокую чувствительность к аддитив-ной помехе. Вычислительные затраты на этапе построения модели (обучения сети) значительны.
Проведенные исследования могут быть полезны при построении систем моделирования, прогнозирования и поддержки принятия решений. Список литературы 1. Демиденко Е.З. Линейная и нелинейная регрессия. - М.: Финансы и статистика, 1981. 2. Круглов В.В., Дли М.И., Голунов Р.Ю. Нечеткая логика и искусственные нейронные сети. - М.: Физматлит, 2001. 3. Дли М.И., Круглов В.В., Осокин М.В. Локально-аппроксимационные модели социально-экономических систем и процессов. - М.: Физматлит, 2000. 4. Demuth H., Beale M. Neural Network Toolbox User’s Guide. The MathWorks, Inc. 2001. 5. Катовник В.Я. Непараметрическая идентификация и сглаживание данных. - М.: Наука, 1985. 6. Медведев А.В. Адаптация в условиях непараметрической неопределенности // Адаптивные системы и их приложения. - Новосибирск: Наука, 1978. - С. 4-34. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=537 |
Версия для печати Выпуск в формате PDF (1.97Мб) |
| Статья опубликована в выпуске журнала № 2 за 2005 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Информационная поддежка технического обеспечения кораблей при первой операции флота
- Методы поисковой адаптации на основе механизмов генетики, самообучения и самоорганизации
- Разработка корпоративной базы в области химии и химической технологии
- Информационная система оптимизации расписания доставки грузов от производителей сырья
- Информационные модели на основе CASE–средств промышленных объектов для информационной поддержки принятия решений
Назад, к списку статей



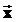 ) и один выход y. Входы и выход данного объекта связаны некоторой нелинейной зависимостью:
) и один выход y. Входы и выход данного объекта связаны некоторой нелинейной зависимостью: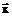 ) + ξ, (1)
) + ξ, (1)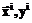 >, i=1, 2, .., N (2)
>, i=1, 2, .., N (2)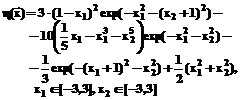 (3)
(3) ном числе радиальных нейронов, реализованный в системе MATLAB [4];
ном числе радиальных нейронов, реализованный в системе MATLAB [4];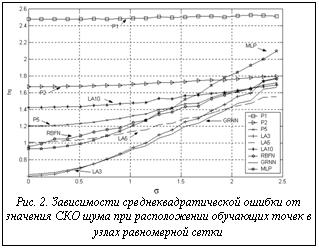 обобщенно-регрессионная нейронная сеть (GRNN) [2] – разновидность искусственной нейронной сети с радиальными базисными функциями (аналогична непараметрической оценке ядерного типа Надарая-Ватсона [5,6]).
обобщенно-регрессионная нейронная сеть (GRNN) [2] – разновидность искусственной нейронной сети с радиальными базисными функциями (аналогична непараметрической оценке ядерного типа Надарая-Ватсона [5,6]).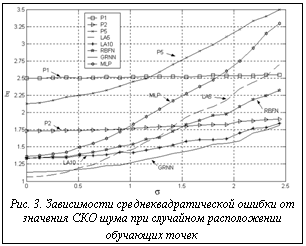 Полученные результаты хотя и являются частными, но в целом отражают общую ситуацию, справедливую для широкого класса объектов.
Полученные результаты хотя и являются частными, но в целом отражают общую ситуацию, справедливую для широкого класса объектов.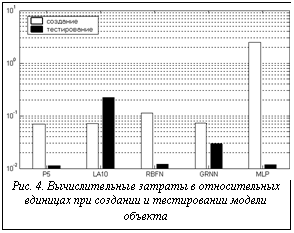 В заключение отметим, что в настоящей статье приводятся результаты экспериментальных исследований наиболее распространенных алгоритмов построения моделей статических объектов, которые показали перспективность по интегральному показателю (точность, чувствительность к аддитивной помехе, вычислительные затраты на создание и тестирование) моделей на основе нейронных сетей с радиальными базисными функциями.
В заключение отметим, что в настоящей статье приводятся результаты экспериментальных исследований наиболее распространенных алгоритмов построения моделей статических объектов, которые показали перспективность по интегральному показателю (точность, чувствительность к аддитивной помехе, вычислительные затраты на создание и тестирование) моделей на основе нейронных сетей с радиальными базисными функциями.