Journal influence
Bookmark
Next issue
The DecernsFMCDA fuzzy multi-criteria decision support system
Abstract:Risk management in the field of environmental protection, remediation of contaminated sites and land use planning requires using modern decision support systems. This paper presents a DecernsFMCDA fuzzy decision support system, which includes both well-known ordinary multicriteria decision analysis methods and original methods for dealing with uncer-tainties based on fuzzy sets and probabilistic approaches. There is an overview of the available com-puter systems for multi-criteria decision analysis, as well as a detailed description of the structure of DecernsFMCDA, its main components and differences from other multi-criteria analysis systems. The paper includes the list of classical, probabilistic and original fuzzy models of multicriteria decision analysis implemented as part of the system, as well as diagrams and descriptions of the general modular architecture of DecernsFMCDA and the original libraries of multicriteria decision analysis (mcda-lib4) and a library for working with fuzzy numbers (fuzzylib). A practical application of the DecernsFMCDA system is shown on the case of the multicriteria problem of finding the optimal method for producing single-wall carbon nanotubes. The problem anal-ysis involves the original fuzzy models FTOPSIS and FMAVT implemented within the framework of the system. The DecernsFMCDA fuzzy decision support system is currently the only system that actu-ally implements all the main methods for solving discrete MADM problems, including dealing with un-certainties. The system allows forming and exploring scenarios using various models of multicriteria decision analysis, including those with different sets of parameters of specified models, for subsequent comparison and analysis of the output results as a part of the decision support process.
Аннотация:Управление рисками при решении экологических проблем, задач охраны окружающей среды, реабилитации загрязненных территорий и планирования землепользования требует применения современных компьютерных систем поддержки принятия решений. В статье представлена компьютерная система поддержки принятия решений DecernsFMCDA, которая включает в себя как широко известные методы многокритериального анализа решений, так и оригинальные подходы к анализу неопределенностей, основанные на применении нечетких множеств и вероятностных методов. Сделан обзор доступных на сегодняшний день компьютер-ных систем многокритериального анализа решений, детально описаны структуры системы поддержки принятия решений DecernsFMCDA и ее основных компонент, а также отличия от других систем, реализующих методы многокритериального анализа решений. Перечислены классические, вероятностные и оригинальные нечеткие модели многокритериального анализа решений, реализованные в составе системы, приведены схемы и описания общей модульной архитектуры DecernsFMCDA и оригинальных библиотек многокритериального анализа решений, а также библиотеки работы с нечеткими числами. Практическое применение DecernsFMCDA рассматривается на примере многокритериальной задачи поиска оптимального способа производства одностенных углеродных нанотрубок, при решении которой используются оригинальные нечеткие модели FTOPSIS и FMAVT, реализованные в рамках системы. В настоящее время DecernsFMCDA является единственной системой, в которой фактически реализованы все основные методы для решения дискретных задач многокритериального анализа решений, в том числе в условиях неопределенности. Система позволяет формировать и исследо-вать сценарии с применением различных моделей многокритериального анализа решений, в том числе с разными наборами параметров заданных моделей, для последующего сравнения и анализа выходных результатов в рамках процесса поддержки принятия решений.
| Authors: Gritsyuk S.V. (s.gritsyuk@gmail.com) - Obninsk Institute for Nuclear Power Engineering – branch of National Research Nuclear University MEPhI, Obninsk, Russia, Ph.D, A.V. Korobov (alexander.korobov.1993@gmail.com) - Obninsk Institute for Nuclear Power Engineering of the National Research Nuclear University "MIPhI", Obninsk, Russia, A.V. Radaev (rad.yyhh@yandex.ru) - Obninsk Institute for Nuclear Power Engineering of the National Research Nuclear University "MIPhI", Obninsk, Russia, Yatsalo B.I. (yatsalo@gmail.com) - Obninsk Institute for Nuclear Power Engineering – branch of National Research Nuclear University MEPhI, Obninsk, Russia, Ph.D | |
| Keywords: decernsfmcda system, decerns project, fuzzy number, fuzzy set, management of risk, uncertainty analysis, multi-criteria decision analysis, decision support system |
|
| Page views: 3718 |
PDF version article |
Принятие решений в различных областях человеческой деятельности, таких как планирование строительства новых объектов, землепользование, защита окружающей среды и многие другие, зависит, как правило, от множества альтернативных решений и критериев для их оценки. Методы анализа решений используются для поиска компромиссов и определения лучших альтернатив (в рамках выбранной/заданной системы ценностей) из множества рассматриваемых вариантов [1]. Системы поддержки принятия решений (ППР) включают в себя реализации различных методов/подходов и полезны, а часто незаменимы, при реализации комплекса оценок и представления входной/выходной информации в рамках решения задач выбора, ранжирования и сортировки аль- тернатив [2]. Среди различных подходов к анализу решений можно выделить классические методы однокритериальной оптимизации (включая методы линейного/нелинейного программирования), методы анализа «затраты–выгода», а также методы многокритериального анализа решений (МКАР) [1, 3, 4]. МКАР – это набор формальных методов, содействующих процессу учета различных критериев при анализе альтернатив и помогающих лицу или группе лиц исследовать и обосновывать те или иные решения. Методы МКАР являются основой многих современных систем ППР [2]. МКАР позволяет интегрировать коли- чественную и качественную информацию, в том числе с учетом неопределенностей объективных данных и/или субъективных суждений. МКАР представляет собой процесс, в котором можно выделить три ключевые фазы [1, 3]. · Идентификация проблемы и структурирование. В начале процесса решения задачи все заинтересованные стороны, включая консультантов по принятию решений (аналитиков, экспертов), вырабатывают общее отношение к рассматриваемой проблеме, ее целям, а также к формированию множества альтернатив и учитываемых критериев, различного рода ограничений и неопределенностей. Структурирование – это идентификация тех факторов и возможных решений, которые должны составить список основных положений для последующего обсуждения и анализа. · Построение модели и ее использование. Исходной и базовой характеристикой МКАР являются формализация и разработка модели (моделей), соответствующей предпочтениям ЛПР/экспертов в рамках рассматриваемых целей, с использованием которой анализ и сравнение альтернатив представляются систематическим и прозрачным процессом. · Принятие решения/разработка плана действий. На основе проведенных оценок, включая анализ неопределенностей, принимается то или иное решение или осуществляется возврат на один из предыдущих этапов МКАР. Таким образом, корректно организованная на основе системного анализа реализация многокритериального анализа представляется процессом, не только оперирующим набором алгоритмов и различного рода аналитическими возможностями, но и ведущим к всесторонней проработке и пониманию природы рассматриваемой задачи. По своим целям задачи (и соответствующие методы) МКАР можно разделить на следующие основные группы [1, 3, 4]: - задачи, направленные на определение наилучшей (компромиссной) альтернативы; - задачи, предназначенные для ранжирования альтернатив; - задачи сортировки, позволяющие разбивать альтернативы на предопределенные упорядоченные группы (например, неприемлемые, приемлемые, частично приемлемые альтернативы); - методы скрининга/фильтрации, направленные на выявление более узкого множества (подмножества) альтернатив для их последую- щего анализа. Кроме того, существуют отдельные методы, направленные на генерацию новых альтернатив, декомпозицию проблемы для ее более глубокого понимания, учет несовпадающих мнений различных экспертов и др.
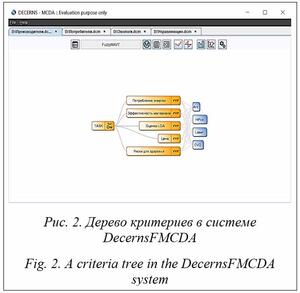
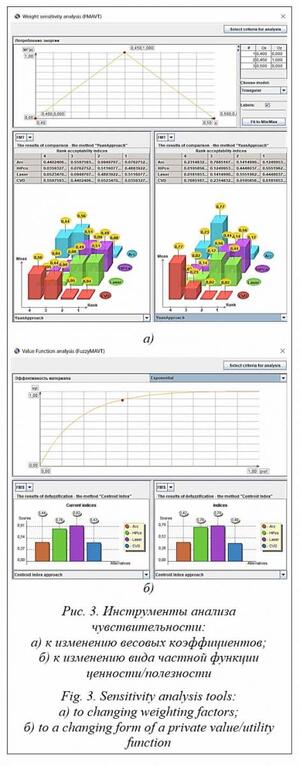
Дискретные методы (Multi-Attribute Decision Making, MADM) применяются для задач с конечным числом заранее заданных альтернатив, в то время как многоцелевые оптимизационные методы (Multi-Objective Decision Making, MODM) – для задач, в которых число альтернатив бесконечно или достаточно велико, а сами альтернативы задаются, как правило, неявно (например, указываются различного рода ограничения, в том числе в форме математических выражений). И одна, и другая группы методов подразделяются на индивидуальные и групповые. Индивидуальные методы подразумевают их реализацию одним экспертом/ЛПР (или однородной группой экспертов, находящихся в согласии или имеющих согласованный подход к решению многокритериальной задачи); групповые методы включают набор специализированных алгоритмов для учета мнений экспертов (заинтересованных лиц/сторон) в реализации всего процесса МКАР. Кроме того, разработаны методы для реализации МКАР в условиях неопределенности объективных значений критериев и субъективных предпочтений/суждений. В рамках данной статьи обсуждаются компьютерные системы (КС), реализующие модели/методы MADM в условиях как определенности, так и неопределенности. Обзор КС для МКАР Методы МКАР и соответствующие КС предлагают широкий спектр подходов к ана- лизу и сравнению альтернатив с использованием объективных и субъективных значений критериев и суждений. Разработан целый ряд академических и коммерческих КС, реализующих различные модели и дополнительные средства для решения всех основных классов задач МКАР [3, 4]. Далее описаны наиболее известные и востребованные КС, реализующие те или иные модели МКАР. · Criterium Decision Plus. Реализует методы MAVT и AHP, обеспечивает структу- рирование задачи с использованием дерева критериев, содержит инструменты анализа чувствительности и (ограниченного) учета неопределенности; доступны версии для веб и ППР в группах. · Decision Lab. Реализует метод PROMETHEE, предоставляет средства визуализации и анализа геометрических данных в пространстве критериев с помощью инструмента GAIA, осуществляет анализ чувствительности к весовым коэффициентам, а также позволяет анализ нескольких сценариев и поддержку принятия групповых решений. · Visual PROMETHEE. Реализует метод PROMETHEE и инструмент визуального анализа GAIA; разработана на замену устаревшему пакету Decision Lab. · Expert Choice. Реализует классический метод AHP, позволяет проводить анализ чувствительности к весам и поддержку групповых решений. · D-Sight. Реализует методы MAUT, AHP, PROMETHEE в рамках веб-системы, доступной с различных устройств. · HIPRE. Реализует методы MAVT и AHP с использованием значений интервальных критериев; доступна веб-версия (Web-HIPRE) для поддержки группового анализа. · SANNA. Приложение для MS Excel; включает методы TOPSIS, ELECTRE I, PROMETHEE II. · Logical Decisions. Реализует методы MAUT и AHP, поддерживает групповой анализ решений, распространяется по бесплатной лицензии. · Decision Deck. Проект представляет собой инициативу по созданию ПО с открытым исходным кодом и обеспечивает процесс разработки различных методов и инструментов MCDA. · Smart Picker Pro. Приложение позволяет ЛПР решать задачи ранжирования и сорти- ровки посредством простого пользователь- ского интерфейса; реализовано как настольное и мобильное приложение; распространяется бесплатно, но опция сохранения проекта приобретается через «встроенные покупки». · AHP Software. Реализует метод AHP, распространяется бесплатно, но регистрация новых пользователей приостановлена (на июль 2021 г.). · JSMAA. Реализует методы SMAA-2 и SMAA-TRI (стохастическая реализация методов MAVT и ELECTRE-TRI на основе концепции приемлемости). · FLINTSTONES. Программный инструмент для решения лингвистических проблем принятия решений в условиях неопределенности; содержит расширения для работы со сложными структурами, такими как многоуровневые лингвистические структуры, разнородные структуры и несбалансированные лингвистические структуры. · DecideIT, Helision. Реализуют средства для моделирования и оценки деревьев критериев, а также деревьев решений для оценки решений в условиях риска; может обрабатывать неточные утверждения с точки зрения интервалов, ранжирования и сравнений посредством метода Delta MCDM; имеет упрощенную веб-версию, доступную под названием Helision. · 1000minds. Использует метод PAPRIKA (оценка относительной важности критериев и альтернатив) для задач ранжирования, приоритизации или выбора альтернатив; реализована как веб-система и может применяться для задач группового анализа решений. Необходимо отметить, что при всем разнообразии описанных КС определенная их часть устарела и/или не поддерживается разработчиками, другие реализуют специфические методы и фактически могут быть использованы только специалистами, а какие-то применяются для решения определенного круга узко- специализированных прикладных задач (финансовых, экологических, медицинских и др.). В то же время ряд КС являются востребованными и весьма популярными у широкого круга пользователей. Среди таких систем можно выделить Criterium Decision Plus, Expert Choice и Decision Lab. Criterium Decision Plus является удобным инструментом как для структурирования многокритериальной задачи с использованием дерева критериев, так и для реализации дальнейшего процесса МКАР с помощью методов (по выбору пользователя) MAVT или AHP [3, 4]; пользователю предоставлены также ограни- ченные возможности учета неопределенностей значения критериев и проведения анализа чувствительности результатов ранжирования альтернатив к изменению весовых коэффициентов критериев. Expert Choice представляет собой классический вариант системы, реализующей метод AHP [4] и ряд средств, включая вопросы иерархической структуры целей/критериев многокритериальной задачи и анализа чувствительности результатов к изменению весовых коэффициентов. В рамках Decision Lab, а также ее наследника Visual PROMETHEE реализован один из наиболее популярных методов МКАР из семейства моделей оценки превосходства – PROMETHEE, включая PROMETHEE I и PROMETHEE II [4]. Гибкий интерфейс системы предоставляет пользователю удобный инструментарий для задания всех параметров модели PROMETHEE, проведения анализа чувствительности к изменению весов критериев, визуального анализа векторных значений моделируемых величин для многокритериальной оценки альтернатив с использованием встроенного инструмента GAIA, а также возможность анализа нескольких сценариев многокритериальной задачи. Особое место в списке используемых для решения научно-прикладных многокритериальных задач занимает JSMAA. Система представляет собой Java-реализацию методов SMAA (Stochastic Multicriteria Acceptability Analysis) с применением алгоритмов Монте-Карло для учета неопределенностей значений критериев и весовых коэффициентов и выбора лучших альтернатив (метод SMAA-2, основанный на использовании модели MAVT), а также сортировки альтернатив (метод SMAA-TRI, представляющий собой стохастическую реализацию модели ELECTRE-TRI) [5, 6]. Одной из известных многокритериальных систем ППР является и разработанная авторами данной статьи DecernsMCDA [7], включающая базовые методы МКАР (MAVT, TOPSIS, AHP, PROMETHEE), а также ряд инструментов для анализа чувствительности. Данная КС эффективно используется в рамках университетского образования и решения научно-практических задач [8]. КС DecernsFMCDA DecernsFMCDA представляет собой настоль- ную систему ППР, включающую реализации различных методов МКАР для решения много- критериальных задач выбора, ранжирования и сортировки альтернатив, в том числе моделей нечеткого МКАР (НМКАР) и дополнительных инструментов ППР. DecernsFMCDA представляет собой существенную модификацию и дальнейшее развитие КС DecernsMCDA [7]. Пользовательский интерфейс DecernsFMCDA. В рамках системы DecernsFMCDA реализованы следующие методы МКАР: - базовые MADM: MAVT [1, 4], AHP [4, 9], TOPSIS [10], PROMETHEE [4] и FlowSort [11]; - MADM на основе вероятностных методов: MAUT [1, 4], ProMAA; - модели НМКАР, являющиеся нечеткими расширениями базовых методов MADM [12]: FuzzyMAVT (FMAVT), FuzzyTOPSIS (FTOPSIS), FuzzyPROMETHEE (FPROMETHEE); - нечеткие модели многокритериальной сортировки альтернатив, являющиеся адаптацией НМКАР-моделей для решения задач сортировки в нечеткой среде: FMAVT-Sort, FTOPSIS-Sort, FPROMETHEE-Sort. Реализация методов MAUT и ProMAA основана на оригинальной библиотеке для вычисления функций от случайной величины (без использования методов Монте-Карло); реализация нечетких методов в DecernsFMCDA основана на оригинальной библиотеке для оценки функций от нечетких чисел (НЧ). Пользователь системы DecernsFMCDA имеет возможность выбрать соответствующий метод МКАР. После исследования задачи различными методами при необходимости может сравнить результаты, что позволяет проводить анализ неопределенностей, связанных с выбранным методом/моделью МКАР/НМКАР [8]. Для эффективной реализации методов МКАР и процесса принятия решений в DecernsFMCDA используются следующие инструменты. · · Таблица характеристик предназначена для загрузки, представления и редактирования данных модели рассматриваемой задачи (см. http://www.swsys.ru/uploaded/image/2022-2/ 2022-2-dop/6.jpg). В DecernsFMCDA реализо- вана расширенная таблица характеристик, которая включает не только матрицу оценок по критериям, но и описание критерия, единицы измерения, свойства шкалы и весовые коэффициенты. · Путь значений предоставляет графики значений критериев для альтернатив, а диаграмма рассеяния представляет значения критериев для альтернатив на двумерной плоскости в соответствии с любыми двумя выбранными критериями; также разработан специальный инструмент для анализа доминирования альтернатив по Парето (альтернатива a1 доминирует a2 по Парето, если по каждому из заданных критериев a1 не хуже, чем a2, и хотя бы по одному из критериев a1 превосходит a2). · Анализ неопределенности в DecernsFMCDA осуществляется на основе анализа чувствительности результатов к изменению весовых коэффициентов и/или функций ценности/полезности, а также принятия во внимание неопределенностей на основе вероятностных методов и нечетких множеств (например, использование различных плотностей вероятности или входных нечетких величин различной формы). Для анализа конкретной многокритериальной задачи пользователи DecernsFMCDA могут сравнить выходные результаты нескольких методов МКАР при наличии соответствующих данных. Такой подход также можно рассматривать как анализ неопределенности к выбору модели МКАР для проведения иссле- дований заданного множества альтернатив. Дерево критериев для рассматриваемой задачи не зависит от выбранного метода МКАР, а таблица характеристик меняет свой вид в зависимости от выбранного метода. Кроме того, инструменты для выбора конкретного метода МКАР и задания весовых коэффициентов поз- воляют создавать различные сценарии для анализа и сравнения. Например, пользователь может создать сценарии с именами MAVT-Ecological-W-S1 и MAVT-Economical-W-S2, назначить метод MAVT для обоих сценариев, но при этом использовать разные наборы весовых коэффициентов (W-S1 и W-S2) и/или другие параметры модели (например, параметры частных функций ценности).
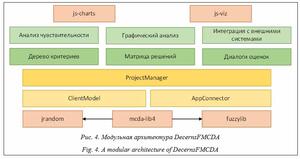
Дерево критериев, матрица решений, диалоги оценок реализованы в виде отдельных графических компонентов. Все компоненты пользовательского интерфейса работают со структурой данных модели ППР, созданием и управлением которой занимается внутренний компонент ProjectManager. В задачи этого компонента входят управление открытыми проектами, создание и сохранение проектов, предоставление доступа к соответствующей проекту модели ППР, которая представлена объектом ClientModel. Данный объект по своей сути является пользовательским/интерфейсным (то есть не содержащим код для расчетов) представлением модели ППР. Посредством объекта AppConnector и разработанной модели событий (описывает все варианты событий, которые могут происходить в системе) данное клиентское представление модели ППР взаимодействует с реализацией математических алгоритмов, формирующих методы ППР. Такое разделение моделей данных, во-первых, позволяет провести четкую декомпозицию на компоненты с разной сферой ответственности, а во-вторых, в случае необходимости перенести приложение в сетевую среду, разделив на серверную и клиентскую части и разработав специализированную версию AppConnector. Расчеты по методам МКАР реализуются библиотекой mcda-lib4, при этом для работы с вероятностными распределениями и нечеткими числами используются специализированные библиотеки jrandom и fuzzylib соответственно. Использование группового анализа решений возможно благодаря интеграции с внешней системой DecernsMCDA-G. Кроме того, поддерживается интеграция с форматом MS Excel и другими табличными форматами данных.
Библиотека ППР mcda-lib4 проектировалась таким образом, чтобы разделять данные и реализации (вычисления) методов МКАР. Такой подход позволяет гибко расширять библиотеку новыми методами. В ее структуре можно выделить несколько основных сущностей: Модель ППР, Критерий, Альтернатива, Категория, Значение, Хранилище данных (Данные), Метод задания весовых коэффициентов, Метод/Модель МКАР. Модель ППР является базовым классом и реализует инструменты для структуризации модели – создания критериев, задания связей между ними, создания альтернатив и категорий. С помощью Хранилищ данных Модель ППР реализует хранение весовых коэффициентов, оценок альтернатив по критериям, профилей категорий в задачах сортировки, оценок попарного сравнения, а также глобальных параметров и параметров критериев. Все методы МКАР, представленные в библиотеке mcda-lib4, реализуются через расширение базового класса Метод и должны представлять специальный набор заранее определенных функций (например, расчет модели, проверка весовых коэффициентов и т.д.). В процессе расчетов Методы обращаются за данными напрямую к Модели ППР, а также используют ряд специализированных классов, например, таких как Метод задания весовых коэффициентов, который реализуют все классы методов взвешивания (задания относительной важности) критериев, поддерживаемых системой: Swing, ранжирование, рейтинг, попарное сравнение, прямой метод, метод энтропии. Оригинальные библиотеки jrandom и fuzzylib предоставляют реализации концепции вероятност- ного распределения и НЧ соответственно, которые используются для представления не- определенностей в вероятностных и нечетких моделях (рис. 5). Анализ чувствительности реализуется за рамками библиотеки mcda-lib4 и может быть представлен как специализированная надстройка/модуль над библиотекой (рис. 4), которая использует встроенные функции сохранения и восстановления состояния модели и многократные расчеты с различными данными для анализа. Методы сортировки, реализованные в библиотеке mcda-lib4, представляют собой специализированные версии классических методов, адаптированных для решения задач сортировки. При этом метод FlowSort [11] можно рассматривать как соответствующую адаптацию метода PROMETHEE к решению задач многокритериальной сортировки. Классические, нечеткие и вероятностные модели МКАР. Классические методы МКАР, реализованные в DecernsFMCDA (рис. 5), описаны в [1, 3, 4], а также в работах авторов данного исследования, например [7]. Вероятностные модели представлены в [4]. В рамках DecernsFMCDA особое внимание уделяется подходам к анализу неопределенностей входных величин при решении приклад- ных задач. Вероятностные модели (MAUT, ProMAA) [4] (рис. 5), использующие распределенные значе- ния критериев или/и весовых коэффициентов и входящие в состав DecernsMCDA [7], были модернизированы (внесены соответствующие изменения в библиотеку mcda-lib4 для оптимизации вычислений разности зависимых случайных величин). Модели НМКАР (FMAVT, FTOPSIS, FPROMETHEE, а также их адаптация к моделям нечеткой многокритериальной сортировки) (рис. 5) являются оригинальными и представлены в работе [12]. Особенностями данных моделей являются возможность использования различных подходов к вычислению функций от НЧ: приближенных методов, основанных на последовательной реализации функций в классе треугольных/трапециевидных НЧ (данный подход используется практически во всех известных приложениях в рамках НМКАР), использование стандартной нечеткой арифметики (вычисления проводятся с использованием заданного количества альфа-срезов, при этом все НЧ рассматриваются как независимые) [14], а также реализация методов трансформации (учитывающих наличие зависимых переменных). В рамках DecernsFMCDA реализованы также основные методы ранжирования НЧ: Centroid Index (CI), Integral of Means (IM), Yuan’s ranking (Y) и их модификации [14].
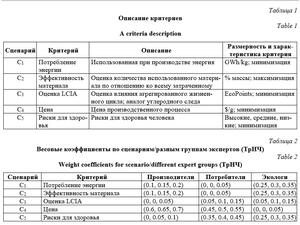
Применение DecernsFMCDA Рссмотрим пример практического примене- ния DecernsFMCDA с использованием нечетких моделей FTOPSIS и FMAVT. В [8] рассмотрена задача поиска оптимального способа производства одностенных углеродных нанотрубок (4 альтернативы и 5 критериев). Одностенные углеродные нанотрубки выдерживают значительные физические воздействия (имеют высокий относительно других доступных материалов предел прочности) и обладают полезными в промышленности электрическими свойствами. Нанотрубки применяются в литий-ионных аккумуляторах, сенсорах, суперкондесаторах и т.д. Так, в кислотно-свинцовых аккумуляторах добавление одностенных нанотрубок значительно увеличивает число циклов перезарядки, что делает нанотрубки очень востребованным материалом. Для решения задачи рассматриваются четыре популярных способа (альтернативы) производства одностенных углеродных нанотрубок [8]: - Arc (A1) – статичный катод и подвижный анод – электрическая дуга, возникающая между катодом и анодом, испаряет анод; - HiPco (A2) – с помощью высокого давления и температур монооксид углерода напыляется на железо (данный метод требует высокой степени очистки); - CVD (A3) – нагретые газы (водород, аргон и метан) используются вместе с катализатором из железа; - Laser (A4) – материал испаряется посредством использования лазера.
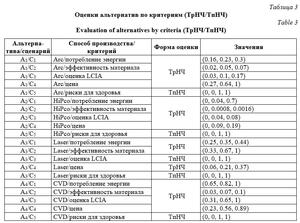
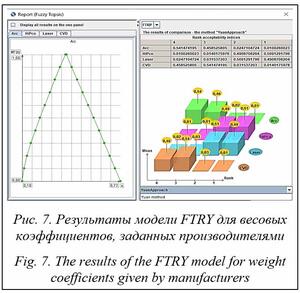
Назначение весовых коэффициентов с использованием треугольных НЧ (ТрНЧ) проводилось следующими группами экспертов: производители, потребители, экологи и управляющие [8] (табл. 2). Оценки альтернатив по критериям представлены в таблице 3 согласно [8]. Для решения рассматриваемой задачи выбраны следующие варианты нечетких моделей FMAVT и FTOPSIS: FMSI (FM обозначает модель FMAVT, S – использование стандартной нечеткой арифметики при вычислении всех функций в модели [14], I – используемый метод ранжирования НЧ), FTRI (FT – модель FTOPSIS, R – редуцированный метод трансформации, применяемый для вычисления функций от НЧ [15], I – используемый метод ранжирования НЧ), I = CI, IM, Y. Таким образом, для решения рассматриваемой многокритериальной задачи с нечеткими данными используются модели FMAVT – FMSCI и FMSIM, а также модели FTOPSIS – FTRCI, FTRIM и FTRY для всех сценариев весовых ко- эффициентов, указанных в таблице 2. Для моделей FMAVT, согласно полученным оценкам (табл. 4), лучшей (компромис- сной) альтернативой является альтернатива А3 для сценариев весовых коэффициентов, заданных производителями и экологами, в то время как для сценария «потребители» ранг 1 имеет альтернатива А2. Для сценария «экологи» ранги 2 и 3 зависят от выбора метода ранжирования.
Таким образом, использование различных моделей, в том числе различных методов ранжирования, может приводить к разным результатам для задач как выбора, так и ранжирования. Методы/модели МКАР/НМКАР могут приводить к различным результатам [3, 7, 13]. Влияние выбора метода ранжирования и/или подхода к оценке функций от НЧ в рамках моделей НМКАР исследуется в работе [13]. При наличии отличий в ранжировании альтернатив различными моделями проводятся детальный анализ чувствительности/неопреде- ленности, переструктурирование многокритериальной задачи, выбор более обоснованной модели для анализа конкретной задачи МКАР/ НМКАР или ряд других подходов. Единственно верного подхода для решения проблем такого рода в общем случае не существует.
Выбор модели МКАР/НМКАР зависит от конкретной многокритериальной задачи, а также опыта и мнений экспертов, решающих ее. Для реализации такого выбора авторы данной работы предлагают использовать комплекс моделей и средств анализа многокритериальных задач, входящих в систему DecernsFMCDA. Заключение Представленная в данной работе система ППР DecernsFMCDA является оригинальной и не имеет аналогов как по набору методов/моделей МКАР, так и по широкому спектру инстру- ментов многокритериального анализа, реализованных в рамках единой программной платформы. Ключевое отличие DecernsFMCDA от других систем МКАР заключается в том, что в настоящее время DecernsFMCDA – единственная система, в которой фактически реализованы все основные методы для решения дискретных задач МКАР, в том числе в условиях неопределенности; гибкая архитектура системы позволяет переходить от одного метода МКАР к другому и после выполнения соответствующих процедур анализа сравнивать полученные результаты для последующего принятия решений. В рамках системы DecernsFMCDA реализован ряд оригинальных моделей нечеткого МКАР (FMAVT, FTOPSIS, FPROMETHEE) для решения многокритериальных задач выбора, ранжирования и сортировки в условиях неопределенности/нечеткости объективных значений критериев и субъективных суждений. Инструментарий DecernsFMCDA позволяет анализировать влияние неопределенностей при задании весовых коэффициентов и частных функций ценности/полезности. DecernsFMCDA зарекомендовала себя как эффективный инструмент ППР при анализе широкого спектра многокритериальных проблем в области управления рисками, экологии, охраны окружающей среды, реабилитации загрязненных территорий, планирования землепользования, экономики и в других сферах. DecernsFMCDA может также эффективно использоваться в рамках целого ряда университетских курсов. Работа выполнена при финансовой поддержке РФФИ в рамках научного проекта № 19-07-01039. Литература 1. Edwards W., Miles R.F., von Winterfeldt D. Advances in Decision Analysis: From Foundations to Applications. NY: Cambridge University Press, 2007. DOI: 10.1017/CBO9780511611308. 2. Marcomini A., Suter G.W., Critto A. Decision Support Systems for Risk-Based Management of Contaminated Sites. NY, Springer Publ., 2009, 436 p. 3. Belton V., Steward T. Multiple Criteria Decision Analysis: An Integrated Approach. MA, Boston, Springer Publ., 2002, 372 p. DOI: 10.1007/978-1-4615-1495-4. 4. Greco S., Ehrgott M., Figueira J.R. Multiple Criteria Decision Analysis. State of the Art Surveys. NY, Springer Publ., 2016, 1048 p. 5. Lahdelma R., Salminen P. SMAA-2: Stochastic multicriteria acceptability analysis for group decision making. Operations Research, 2001, vol. 49, no. 3, pp. 444–454. DOI: 10.1287/OPRE.49.3.444.11220. 6. Tervonen T., Figueira J.R. A survey on stochastic multicriteria acceptability analysis methods. JMCDA, 2008, vol. 15, pp. 1–14. DOI: 10.1002/MCDA.407. 7. Яцало Б.И., Грицюк С.В., Диденко В.И., Мирзеабасов О.А. Система многокритериального анализа решений DecernsMCDA и ее практическое применение // Программные продукты и системы. 2014. № 2. С. 73–84. 8. Linkov I., Moberg E., Trump B.D., Yatsalo B., Keisler J.M. Multi-Criteria Decision Analysis. Case Studies in Engineering and the Environment. Environmental Assessment and Management. USA, CRC Press Publ., 2021, 420 p. 9. Saaty T.L. The analytic hierarchy and analytic network processes for the measurement of intangible criteria and for decision-making. In: Multiple Criteria Decision Analysis, 2016, pp. 363–419. DOI: 10.1007/978-1-4939-3094-4_10. 10. Opricovic S., Tzeng G.-H. Compromise solution by MCDM methods: a comparative analysis of VIKOR and TOPSIS. European J. of Operational Research, 2004, vol. 156, pp. 445–455. DOI: 10.1016/S0377-2217(03)00020-1. 11. Nemery P., Lamboray C. FLOWSORT: A flow-based sorting method with limiting or central proles. TOP, 2008, vol. 16, pp. 90–113. DOI: 10.1007/s11750-007-0036-x. 12. Yatsalo B., Korobov A., Martinez L. Fuzzy multi-criteria acceptability analysis: A new approach to multi-criteria decision analysis under fuzzy environment. Expert Systems with Applications, 2017, no. 84, pp. 262–271. DOI: 10.1016/j.eswa.2017.05.005. 13. Yatsalo B., Korobov A., Radaev A., Qin J., Martinez L. Ranking of independent and dependent fuzzy numbers and intransitivity in fuzzy MCDA. IEEE Transactions on Fuzzy Systems, 2021. DOI: 10.1109/tfuzz.2021.3058613. 14. Dubois D., Prade H. Fuzzy Sets and Systems: Theory and Applications. Mathematics in Science and Engineering. Academic Press, 1980, 393 p. 15. Hanss M. Applied fuzzy arithmetic: An introduction with engineering applications. Choice Reviews Online, 2005, vol. 43, no. 4, pp. 43–2258. DOI: 10.5860/choice.43-2258. References
|
| Permanent link: http://swsys.ru/index.php?page=article&id=4893&lang=en |
Print version |
| The article was published in issue no. № 2, 2022 [ pp. 171-183 ] |
Perhaps, you might be interested in the following articles of similar topics:
- Система многокритериального анализа решений DecernsMCDA и ее практическое применение
- Модуль группового многокритериального анализа решений на основе нечеткого расширения метода TOPSIS
- F-Ranking: компьютерная система для ранжирования нечетких чисел
- Анализ систем обработки информации и управления с помощью групповых нечетких чисел
- Диагностика блоков атомных станций с применением многоагентного подхода
Back to the list of articles