Химическая реакция является сложным явлением, и для ее успешного моделирования необходимо точно сформулировать задачу и выявить ключевые факторы, имеющие определяющие значения для модели. Введем формальное описание химических реакций (ХР), необходимое для формулирования задачи.
Пусть имеется ХР c набором исходных веществ {S1, S2, …, Sm}, в результате которой образуется совокупность продуктов {P1, P2, …, Pn}. Возможность протекания данной реакции и степень превращения исходных веществ существенно зависят от набора условий {c1, c2, …, ck}, в которых протекает данная реакция. Под ними подразумеваются физические ус- ловия (давление, температура), исходные концентрации веществ, катализаторы, растворители и т.д.
Количественной характеристикой протекания ХР является выход ее продуктов – отношение фактического количества продукта к теоретически возможному:
 (1)
(1)
где mif – фактический выход продукта; mit – тео- ретический выход продукта. Так как mit > mif, то wi Î [0, 1]. Очевидно, что wi является функцией от условий и времени проведения реакции:
wi = F(c1, c2, …, ck, t). (2)
В большинстве случаев время t проведения одной и той же реакции постоянно, тогда как выходы продуктов реакции будут зависеть только от набора конкретных условий.
В ряде случаев имеется накопленный экспериментальный материал о протекании реакции в различных условиях, на основе которого можно сформировать оценку эффективности для условий {c1, c2, …, ck}. Для получения оценок можно использовать нейронные сети (НС). В настоящее время НС активно применяются в современной химии для прогнозирования свойств индивидуальных веществ [1–3] и возможности протекания ХР [4–6].
Применение НС в интересах прогнозирования идет по двум направлениям – прогноз возможности взаимодействия субстратов без учета условий и катализаторов [5, 6] и прогноз протекания процессов в зависимости от состава системы [4].
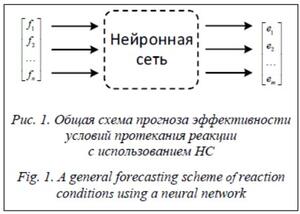 На рисунке 1 показана применяемая в данной работе общая схема использования НС для прогноза эффективности условий ХР. Пусть имеется вектор {f1, f2, …, fn}, кодирующий условия протекания реакции. Тогда на его основе сформированная и обученная НС выдаст оценку эффективности условий в виде выход- ного вектора {e1, e2, …, em}.
На рисунке 1 показана применяемая в данной работе общая схема использования НС для прогноза эффективности условий ХР. Пусть имеется вектор {f1, f2, …, fn}, кодирующий условия протекания реакции. Тогда на его основе сформированная и обученная НС выдаст оценку эффективности условий в виде выход- ного вектора {e1, e2, …, em}.
В зависимости от условий и степени детализации данных об условии вектор {f1, f2, …, fn} может быть задан в бинарном виде либо содержать числовые значения, характеризующие параметры.
Выходные значения {e1, e2, …, em} кодируют эффективность условий протекания ХР. Например, выходной вектор может содержать прогнозируемые выходы продуктов ХР за время t, при этом производится аппроксимация функции (2). Также выходной вектор может со- держать бинарные данные и классифицировать условия (например, в конкретных условиях реакция не протекает, или протекает с низким выходом, или протекает практически полностью).
Кодирование данных об условиях протекания реакции
Данные о протекании ХР можно разделить на три большие группы: компоненты ХР, условия протекания реакции и физические условия. На рисунке 2 показана иерархия данных. В виде эллипса изображены вводные данные, которые можно кодировать в бинарном виде, в виде прямоугольника – данные, которые подразумевают формирование входных векторов на основе числовых параметров. Если некоторое условие протекания реакции сi кодируется вектором значений fi = {f1i, …, fki}, то результирующий входной вектор будет конкатенацией векторов f1 • … • fn.
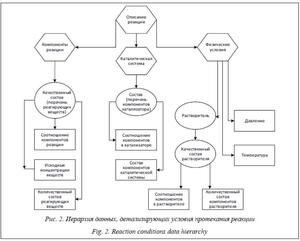
Основной вопрос составляет методика кодирования химических веществ. Существуют различные подходы при кодировании информации о строении и свойствах веществ с различной степенью детализации о составе всех участников химического процесса.
Пусть имеется набор p веществ, которые используются в качестве катализаторов некоторой реакции. Простейшим способом кодирования является бинарный вектор b; bi = 1, если конкретные условия предполагают использование вещества i, bi = 0 в противном случае. Если катализатор составной (содержит смесь веществ), то количество единичных элементов в векторе b будет равно количеству веществ в каталитической системе. Кроме того, для составных катализаторов можно ввести вектор d, каждый элемент которого содержит долю вещества i в каталитической системе. Пусть для каждого вещества мы знаем брутто-формулу, то есть количество атомов, входящих в состав каждого компонента. Данный способ кодирования детализирует состав веществ, хотя и не решает проблему изомеров (веществ, имеющих одинаковый состав, но разное химическое строение). Аналогичный способ кодирования можно применить для средообразователей.
Архитектура НС для прогноза
Для прогноза эффективности условий проведения ХР в данной работе использована НС с архитектурой многослойный персептрон. Персептрон состоит из формальных нейронов (ФН), которые организованы в слои. ФН каждого слоя соединены с нейронами соседних слоев по принципу «каждый с каждым» [7–9], при этом выходной сигнал каждого нейрона определяется формулой
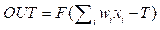 , (3)
, (3)
где wi – весовые коэффициенты; xi – входные сигналы нейрона; T – пороговое значение данного нейрона; F – функция активации нейрона; OUT – выходной сигнал. В качестве функции активации часто используется сигмоида
 (4)
(4)
где OUT – выходной сигнал нейрона; NET – входной сигнал.
В работе применялись НС с одним скрытым слоем. Для обучения НС использовался алгоритм обратного распространения ошибки (Backpropagation algorithm) [5–7].
Алгоритм обратного распространения ошибок предполагает на каждой итерации обучения проведение коррекции весовых коэффициентов и пороговых значений каждого ФН по формулам:
Dwij = e(dj – yj)xij, DTj = –e(dj – yj), (5)
где e – некоторое положительное число (learning rate), определяющее скорость обучения. В зависимости от реализации алгоритма обратного распространения e может быть константой либо функцией от номера итерации обучения e = f(i).
В данной работе при обучении НС использовались как константное значение e, так и функция
e(i) = 1/ai, (6)
где a – константа, определяющая скорость уменьшения значений e от номера итерации.
При решении задач классификации активно применяются НС Кохонена – особый тип НС, содержащих слой Кохонена, состоящий из адаптивных линейных сумматоров (линейных ФН). Применяющиеся в данной работе слои Кохонена обрабатывают выходные сигналы по правилу «Победитель получает все»: наибольший сигнал превращается в единичный, остальные – в ноль.
Прогноз эффективности условий реакции с использованием НС на примере реакции карбонилирования олефинов
Реакция карбонилирования олефинов является важной промышленной реакцией, широко применяемой в фармацевтической промышленности при производстве нестероидных жаропонижающих препаратов. Данная реакция описывается уравнением Olefine + CO + + H2O → A + B, где A – основной продукт; B – побочный продукт. Реакция протекает в присутствии различных катализаторов, но проведение ее в наиболее мягких условиях обеспечивает присутствие комплексов палладия (II) в качестве катализатора [10, 11].
Прогноз активности промотора. При проведении реакции карбонилирования актив- ность палладиевого катализатора существенно повышается введением промотора (вещества, не обладающего отдельной каталитической активностью, но повышающего активность катализатора). Имеется информация об использовании в качестве промотора вещества состава MeXn, Me ∈ {Cu, Ni, Zn, Sn, W}, X ∈ {Cl, CO}.
Для прогноза активности промотора был обучен персептрон со слоем Кохонена, содержащий один скрытый слой (4 нейрона) и один выходной слой (3 нейрона).
Входными сигналами являлись четыре параметра: {{Np, Ng}, {NСl, NCO}}. Металл закодирован двумя цифрами – номер группы Ng и номер периода Np в таблице Менделеева, тип и количество лигандов Cl и CO.
Выходные параметры: прогнозируемая эффективность промотора, закодированная тремя булевыми значениями:
{0, 0, 1} – низкая эффективность;
{0, 1, 0} – средняя эффективность;
{1, 0, 0} – высокая эффективность.
Прогноз эффективности катализатора. В таблице 1 приведены результаты оценки эффективности соединений LaCl3 и LaCl3, которые были выделены в контрольную выборку и не применялись в обучении.
Таблица 1
Прогнозируемая эффективность промоторов состава MeXn, Me ∈ {Cu, Ni, Zn, Sn, W}, X ∈ {Cl, CO}
Table 1
Predictive efficiency of the combination promoter MeXn, Me ∈ {Cu, Ni, Zn, Sn, W}, X ∈ {Cl, CO}
|
Формула
|
Np
|
Ng
|
NCO
|
NCl
|
Выход
|
|
FeCl3
|
4
|
8
|
0
|
3
|
0, 1, 0
|
|
LaCl3
|
6
|
3
|
0
|
3
|
1, 0, 0
|
Как показано в таблице, НС корректно классифицировала активность промотора, основываясь на брутто-формуле последнего.
Прогноз эффективности системы «Растворитель–Катализатор». В соответствии с экспериментальными данными для реакций карбонилирования используются катализатор PdLn, L∈ (OAc, Cl, PPh3, PhCN, Py), и растворитель вида AnCm, A ∈ (Cl, Br, PF6, AlF4), C ∈ (TBA, BMIM). Сформирован и обучен персептрон со слоем Кохонена. Сеть содержит один скрытый слой (10 нейронов) и один выходной слой (4 нейрона). При обучении применялся алгоритм обратного распространения ошибки.
Входные параметры: {{NOAc, NCl, NPhCN, NPy, NPPh3}, {NCl, NBr, NTBA, NBMIM, other}}.
Тип лиганда L и его количество в катализаторе закодированы в первом подмножестве NOAc, NCl, NPhCN, NPy, NPPh3, во втором подмножестве закодирован состав растворителя.
Выходные параметры: прогнозируемая эффективность системы «Катализатор-ИЖ», закодированная четырьмя булевыми значениями:
{0, 0, 0, 1} – выход < 30 %;
{0, 0, 1, 0} – выход в интервале [30, 50];
{0, 1, 0, 0} – выход в интервале (50, 80];
{1, 0, 0, 0} – выход в интервале (80, 80].
В таблице 2 приведены результаты оценки эффективности ряда каталитических систем.
Таблица 2
Прогноз эффективности системы «Растворитель–Катализатор»
Table 2
The system efficiency forecast “Dissolving agent–Accelerant”
|
Состав
|
Катализатор
|
Растворитель
|
Прогноз
|
|
Pd(OAc)2, TBABr
|
2, 0, 0, 0, 0
|
0, 1, 0, 1, 0
|
0, 0, 0, 1
|
|
PdCl2(PPh3)2, TBABr
|
0, 2, 0, 0, 2
|
0, 1, 0, 1, 0
|
0, 1, 0, 0
|
|
Pd(PPh3)4, TBACl
|
0, 0, 0, 0, 4
|
1, 0, 0, 1, 0
|
1, 0, 0, 0
|
Прогноз выходов реакции карбонилирования стирола на основе исходных концентраций компонентов. Для прогноза выходов был разработан модуль для расчета изменения концентраций во времени на основе кинетических моделей (решение прямой кинетической задачи). Данный модуль производит перерасчет концентрации методом Эйлера за указанный период времени. Результаты данного расчета используются для обучения НС. Общая схема моделирования показана на рисунке 3. Для хранения и работы с нейросетевыми моделями использовалась специальная информационная система [12].
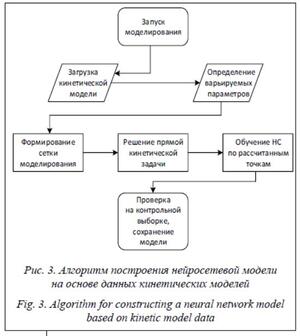
Выбраны параметры модели:
- давление P (от 4 до 8 атмосфер);
- концентрация стирола (от 1 200 до 1 800 кмоль/м3);
- концентрация катализатора (от 0.3 до 0.8 кмоль/м3).
Расчет проводился на основе кинетической модели [13]. В данной модели предполагается прогноз выхода только основного продукта реакции (гидратроповой кислоты).
На первом этапе формировалась сетка условий, обеспечивающая равномерное распределение входных параметров. Далее проводился расчет выходов по кинетической модели. Выход продуктов рассчитывался спустя 120 минут после начала реакции. Затем производилось обучение НС на выборках различного размера, при этом каждая десятая точка попадала в контрольную выборку.
Первый эксперимент по обучению НС включал попытку прогнозировать значение выхода целевого продукта. В таблице 3 представлены результаты прогноза на тестовой выборке с помощью НС с одним скрытым слоем, где Ndata – размер выборки, Ncycles – количество циклов обучения НС, Nn – количество нейронов в скрытом слое. Обучение проводилось с использованием формулы (6) для вычисления коэффициента, при этом был выбран параметр a = 0.1. Для оценки точности рассчитывалась ошибка аппроксимации по формуле
 (7)
(7)
 где N – размер контрольной выборки; wi – целевое значение выхода (из тестовой выборки); yi – прогнозируемый выход.
где N – размер контрольной выборки; wi – целевое значение выхода (из тестовой выборки); yi – прогнозируемый выход.
Как показано в таблице 3, с увеличением количества циклов обучения увеличивается точность аппроксимации. С увеличением количества ФН в скрытом слое в значительном количестве случаев также повышается точность аппроксимации. Количество циклов обучения НС также увеличивает точность прогноза. Размер выборки в данном случае не оказывал существенного влияния на точность прогноза.
 Также НС была обучена классификации условий проведения реакции (по значениям выхода основного продукта). Для этого в НС был введен слой Кохонена. Выходной вектор при этом кодирует условия проведения реакции следующим образом:
Также НС была обучена классификации условий проведения реакции (по значениям выхода основного продукта). Для этого в НС был введен слой Кохонена. Выходной вектор при этом кодирует условия проведения реакции следующим образом:
- хорошие условия (выход целевого продукта w > 0.8);
- средние условия (выход целевого продукта 0.8 > w > 0.5);
- плохие условия (выход целевого продукта w < 0.5).
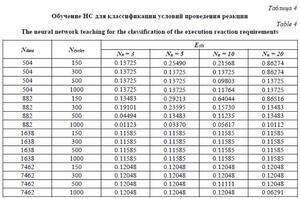 Данные по обучению НС со слоем Кохонена приведены в таблице 4. При обучении использовалось постоянное значение коэффициента обучения e = 0.5. Ошибка классификации рассчитывалась как отношение количества ошибок к размеру контрольной выборки:
Данные по обучению НС со слоем Кохонена приведены в таблице 4. При обучении использовалось постоянное значение коэффициента обучения e = 0.5. Ошибка классификации рассчитывалась как отношение количества ошибок к размеру контрольной выборки:
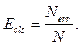 (8)
(8)
Как показано в таблице 4, обучение НС для классификации условий проведения реакции в большинстве экспериментов имеет ошибку больше 10 %. При этом увеличение числа ФН в скрытом слое не приводит к увеличению точности, а для ряда экспериментов, наоборот, снижает точность классификации. При размере выборки свыше 1 000 значений обучение приводит к постоянной ошибке вне зависимости от количества ФН в скрытом слое и количества циклов обучения.
Выводы
Очевидно, что НС являются удобным инструментом, позволяющим прогнозировать протекание ХР в определенных условиях. Особое внимание уделено кодированию данных об условиях проведения реакции для обучения и непосредственного прогноза. Задачи прогноза эффективности условий разделены на две группы: классификация условий по выходу конечного продукта и аппроксимация выхода на основе данных об условиях протекания ХР.
Построено несколько нейросетевых моделей для прогноза влияния условий на протекание реакции карбонилирования олефинов. Для обучения НС использовались как экспериментальные данные о протекании реакций, так и результаты моделирования данной реакции. В результате НС были успешно обучены классификации промоторов и растворителей на основе их элементарного состава (брутто-формулы), а также аппроксимации с хорошей точностью выхода продукта реакции карбонилирования стирола.
Для проведения компьютерного эксперимента была разработана программа, позволяющая подготавливать входные данные для моде- лирования, а также непосредственно обучать НС.
Литература
1. Halberstam N.M., Baskin I.I., Palyulin V.A., Zefirov N.S. Neural networks as a method for elucidating structure-property relationships for organic compounds. Russian Chemical Reviews, 2003, vol. 72, no. 7, pp. 629–649. DOI: 10.1070/RC2003v072n07ABEH000754.
2. Baskin I.I. Machine learning methods in computational toxicology. Methods in molecular biology, 2018, vol. 1800, pp. 119–139. DOI: 10.1007/978-1-4939-7899-1_5.
3. Wu Y., Wang G. Machine learning based toxicity prediction: from chemical structural description to transcriptome analysis. J. of Molecular Sciences, 2018, vol. 19, no. 8, art. 2358. DOI: 10.3390/ijms19082358.
4. Te Su H., McAvoy T.J., Werbos P. Long-term predictions of chemical processes using recurrent neural networks. A parallel training approach. Ind. Eng. Chem. Res., 1992, vol. 31, no. 5, pp. 1338–1352. DOI: 10.1021/ie00005a014.
5. Wei J.N., Duvenaud D., Aspuru-Guzik A. Neural networks for the prediction of organic chemistry reactions. ACS Cent. Sc., 2016, vol. 2, no. 10, pp. 725–732. DOI: 10.1021/acscentsci.6b00219.
6. Coley C.W., Jin W., Rogers L., Jamison T.F., Jaakkola T.S., Green W.H., Barzilay R., Jensen K.F. A graph-convolutional neural network model for the prediction of chemical reactivity. Chem. Sci., 2019, vol. 2, no. 10, pp. 370–377. DOI: 10.1039/c8sc04228d.
7. Stephen I., Gallant S.I. Neural network learning and expert systems. The MIT Press, 1994, vol. 7, iss. 3–4, pp. 238–240.
8. Rojas R. Neural Networks. Springer-Verlag, Berlin, 1996, 524 p.
9. Hagan M.T., Demuth H.B., Beale M.H. Neural Network Design. PWS Publ., Boston, 1996.
10. Eliseev O.L., Stepin N.N., Bondarenko T.N., Lapidus A.L. Phosphine-free catalytic system for the carboxylation of olefins with carbon oxide. Doklady Chemistry, 2005, vol. 401, iss. 4–6, pp. 59–61. DOI: 10.1007/s10631-005-0032-3.
11. Lapidus A.L., Eliseev O.L., Bondarenko T.N., Chau N.H. Hydroxy- and alkoxycarbonylation of ethylene in molten salt medium. Proc. DGMK/SCI Conf., Dresden, Germany, 2009, pp. 225–231.
12. Звягинцев Н.В., Биллиг В.А. Информационная система обработки и хранения данных о кинетике химических реакций // Программные продукты и системы. 2018. Т. 31. № 4. С. 808–813. DOI: 10.15827/0236-235X.124.808-813.
13. Li Y., Chaudhari R.V. Kinetic modeling of hydroxycarbonylation of styrene using a homogeneous palladium complex catalyst. Ind. Eng. Chem. Res., 2011, vol. 50, no. 16, pp. 9577–9586. DOI: 10.1021/ ie200676h.
References
- Halberstam N.M., Baskin I.I., Palyulin V.A., Zefirov N.S. Neural networks as a method for elucidating structure-property relationships for organic compounds. Russian Chemical Reviews. 2003, vol. 72, no. 7,
pp. 629–649. DOI: 10.1070/RC2003v072n07ABEH000754.
- Baskin I.I. Machine learning methods in computational toxicology. Methods in Molecular Biology. 2018, vol. 1800, pp. 119–139. DOI: 10.1007/978-1-4939-7899-1_5.
- Wu Y., Wang G. Machine Learning Based Toxicity Prediction: from chemical structural description to transcriptome analysis. Int. J. Mol. Sci. 2018, vol. 19, no. 8, art. 2358. DOI: 10.3390/ijms19082358.
- Te Su H., McAvoy T.J., Werbos P. Long-term predictions of chemical processes using recurrent neural networks. A parallel training approach. Ind. Eng. Chem. Res. 1992, vol. 31, no. 5. DOI: 10.1021/
ie00005a014.
- Wei J.N., Duvenaud D., Aspuru-Guzik A. Neural networks for the prediction of organic chemistry reactions. ACS Cent. Sci. 2016, vol. 2, no. 10, pp. 725–732. DOI: 10.1021/acscentsci.6b00219.
- Coley C.W., Jin W., Rogers L., Jamison T.F., Jaakkola T.S., Green W.H., Barzilay R., Jensen K.F.
A graph-convolutional neural network model for the prediction of chemical reactivity. Chem. Sci. 2019,
vol. 2, no. 10, pp. 370–377. DOI: 10.1039/c8sc04228d.
- Stephen I. Gallant S.I. Neural network learning and expert systems. The MIT Press. 1994, vol. 7,
iss. 3–4, pp. 238–240.
- Rojas R. Neural Networks. Springer-Verlag, Berlin, 1996, 524 p.
- Hagan M.T., Demuth H.B., Beale M.H. Neural Network Design. PWS Publ., Boston, 1996.
- Eliseev O.L., Stepin N.N., Bondarenko T.N., Lapidus A.L. Phosphine-free catalytic system for the carboxylation of olefins with carbon oxide. Doklady Chemistry. 2005, vol. 401, iss. 4–6, pp. 59–61. DOI: 10.1007/s10631-005-0032-3.
- Lapidus A.L., Eliseev O.L., Bondarenko T.N., Chau N.H. Hydroxy- and alkoxycarbonylation of ethylene in molten salt medium. Proc. DGMK/SCI Conf. Dresden, Germany, 2009, pp. 225–231.
- Zvyagintsev N.V., Billig V.A. Information system for processing and storing information on chemical reaction kinetics. Software & Systems. 2018, vol. 31, no. 4, pp. 808–813. DOI: 10.15827/0236-235X.124.808-813 (in Russ.).
- Li Y., Chaudhari R.V. Kinetic modeling of hydroxycarbonylation of styrene using a homogeneous palladium complex catalyst. Ind. Eng. Chem. Res. 2011, vol. 50, no. 16, pp. 9577–9586. DOI: 10.1021/
ie200676h.





