Journal influence
Bookmark
Next issue
A comparative analysis of methods of calculation the number Pi by standard means
Abstract:The process of the research on finding the number Pi can be divided into three periods: the ancient period, the classical era and the era of modern computers. Each of them has its own methods and tools. The purpose of this work is to analyze and compare various methods of calculating the number Pi using standard tools: MS Excel spreadsheet and Free Pascal programming environment. Computational methods are based on mathematical expressions, which are a qualitative approximation of the number Pi. They are the series of Gregory-Leibniz, Madhava, Neelakant, Euler's and Wallis's formulas, etc. The comparative analysis of these expressions and algo-rithms created on their basis has revealed the fastest and exact method of finding thhe number Pi. The paper describes computational studies, the result of which is finding the number Pi accurate within the 10th decimal place. The pur-pose of this study was to determine which computing environment is more accurate and effective for finding the number Pi. Based on the study results, there is a comparative analysis of MS Excel and Free Pascal computational capabilities regarding laboriousness, calculation time and Pi number computing accuracy. The originality of the work is in calculation of the sum of a series that converges to Pi for each new place of summands. Thus, the author shows in practice the dynamics of series convergence to the number Pi. For each of these approximate values of Pi, the absolute and relative errors are calculated. The number of summands is chosen based on calculation accuracy, which is considered satisfactory if the relative error is <0.001%.
Аннотация:Процесс исследования нахождения числа Пи можно разделить на три периода: древний период, классическая эра и эра современных компьютеров. Каждый из них характеризуется своими методами и инструментами. Цель данной работы заключается в анализе и сравнении различных методов вычисления числа Пи с использованием стандартных инструментов – табличного процессора MS Excel и среды программирования Free Pascal. В основе вычислительных методов лежат математические выражения, которые являются качественной аппроксимацией числа Пи. Это ряды Грегори–Лейбница, Мадхавы, Нилаканта, формулы Эйлера и Валлиса и другие. Сравнительный анализ этих выражений и алгоритмов, созданных на их основе, позволил выявить самый быстрый и точный метод нахождения числа Пи. Результатом проведенных исследований вычислительного характера стало нахождение числа Пи с точностью до 10-го знака после запятой. Указанные вычисления были выполнены в табличном процессоре MS Excel и программной среде Free Pascal. Цель данного исследования состояла в том, чтобы выяснить, какая из вычислительных сред является более точной и эффективной для нахождения числа Пи. По результатам исследования представлен сравнительный анализ вычислительных возможностей MS Excel и Free Pascal относительно трудоемкости, времени расчетов и точности вычислений числа Пи. Оригинальность работы состоит в том, что для каждого нового разряда слагаемых вычисляется сумма ряда, которая сходится к Пи. Таким образом, показана динамика сходимости рядов к числу Пи на практике. Для каждого из этих приближенных значений числа Пи рассчитаны абсолютная и относительная ошибки. Количество слагаемых выбирается, исходя из точности вычислений, которая считается удовлетворительной, если относительная ошибка < 0,001 %.
| Authors: Bakaeva, O.A. (helga_rm@rambler.ru) - Mordovian State Pedagogical Institute (Associate Professor), Saransk, Russia, Ph.D | |
| Keywords: number pi, sum of series, ms excel, free pascal, relative error, absolute error |
|
| Page views: 9561 |
PDF version article Full issue in PDF (19.46Mb) |
Число Пи ‒ одна из фундаментальных математических констант, равная отношению длины окружности к ее диаметру в пространстве с евклидовой метрикой. Значение 3,14 является достаточно приблизительным и используется для обучения и простоты расчетов. На данный момент известны триллионы знаков после запятой у этой константы. Данное число появляется в формулах и расчетах, используемых во многих сферах: в физике, космосе, электротехнике, электронике, теории вероятностей, строительстве, навигации и пр. Причем с развитием техники и увеличением вычислительных мощностей современных компьютеров открываются новые возможности исследования самой константы и ее практического применения. На протяжении всей истории математической науки не прекращается работа по уточнению значения числа Пи. О том, насколько далеко продвинулась математика, можно судить по количеству десятичных знаков числа, которое удалось определить на данном историческом этапе. Хронологическое развитие процесса вычисления числа Пи. Процесс исследования этой константы можно разделить на три периода: древний период (геометрическая интерпретация числа Пи), классическая эра (теория рядов, пределы и интегралы ‒ после становления математического анализа) и эра современных компьютеров. Древний период вычисления числа Пи. Еще в древности математики знали, что вычисление зна- чения π и площади круга − задачи, тесно связанные между собой [1]. Древние китайцы и евреи считали число π равным 3. В древнеегипетском папирусе писца Ахмеса значение числа π ≈ 3,1605, в Вавилоне π оценивалось как 25/8 ≈ 3,125, а в самом Египте как 256/81 ≈ 3,160 (1850 г. до н.э.). Архимед путем многократного описывания вокруг окружности и вписывания в нее правильных многоугольников получил π ≈ 3,142857142857143. В средние века были получены следующие результаты: 339/108 ≈ 3,139 (Индия, IX в. до н.э.); 3,1416 ‒ Лю Хуэй (Китай, 263 г.); 3,1415926 < π < < 3,1415927 ‒ Цзу Чунчжи (Китай, ок. 480 г.) [2]. В дальнейшем точность вычисления числа Пи определялась уже десятками знаков после запятой. Практически все вычисления на данном этапе были связаны с представлением числа π в виде дроби, которая давала большую погрешность, и имели геометрическую интерпретацию. Классическая эра. В это время происходит научное становление числа Пи. Обозначение π вводит британский математик Джонс в 1706 году, а общепринятым оно становится после работ Л. Эйлера в 1737 году. В XVIII–XIX вв. были произведены расчеты, в результате которых получены сотни знаков в дробной части. Развитие математического анализа в XVII веке привело к открытию многих рядов, сумма которых с увеличением числа слагаемых, но с различной по- грешностью, стремилась к Пи. К таким рядам относятся следующие: ряд Грегори–Лейбница, ряд Мадхавы (уточнение ряда Грегори–Лейбница), ряд Нилаканта, формула Эйлера, формула Валлиса, формула Дж. Мэчина с разложением функции arctg(x) в ряд Тейлора, рекурсивная формула Виета с использованием выражения Ö2. Существуют и другие, более сложные выражения для вычисления числа Пи. К ним относятся ряды, пределы, интегралы и малоизвестные математические взаимосвязи числа Пи и различных функций [3–5]. Эра цифровых компьютеров. Начиная с середины ХХ века, с момента внедрения компьютеров в научные исследования, число Пи удалось вычислить с колоссальной точностью: Джон фон Нейман (США, 1949 г., ENIAC), Франсуа Женюи (Франция, 1959 г., IBM704), Джин Гийу и Мартин Буйе (Франция, 1973г. CDC 7600), братья Чудновские (США, 1989 г., IBM3090), Ясумаса Канада (Япония, 2002 г., HITACHI, SR8000/MPP), Александр Йи и Сингэру Кондо (Япония, десктоп 2×Intel Xeon Х). Одной из перспективных формул недавнего времени стала формула Бэйли–Боруэйна–Плаффа, открытая С. Плаффом [6, 7]. Особенность этой формулы в том, что она позволяет извлечь любую конкретную шестнадцатеричную или двоичную цифру числа Пи без вычисления предыдущих. В настоящее время существуют различные подходы к вычислению числа Пи, в основе которых часто лежит физический смысл [8] или так называемая длинная арифметика [9]. Материалы и методы. Цель данной работы в том, чтобы проанализировать и сравнить различные методы вычисления числа Пи с использованием стандартных инструментов: табличного процессора MS Excel и среды программирования Free Pascal. Для моделирования вычисления числа Пи могут использоваться различные программные средства: табличный процессор MS Excel, языки программирования Free Pascal, C++, пакеты ком- пьютерной математики MathCAD, MATLAB и др. Моделирование вычисления числа Пи чаще всего сводится к нахождению суммы ряда. А все указанные программные средства позволяют осуществлять необходимые расчеты [10, 11]. Понятно, что нахождение числа π ≈ 3 и даже π = 3,14 не станет открытием. Но, увеличивая количество слагаемых в математической формуле и число итераций в программе, можно получить любое количество знаков в дробной части числа и необходимую точность. Тем самым выяснится, какой из методов вычисления числа Пи самый точный и какой инструмент из доступных вычислительных средств является самым эффективным для этого конкретного метода и для всего данного вида исследований. Для моделирования вычисления числа Пи используются стандартные вычислительные средства: табличный процессор MS Excel и язык про- граммирования Free Pascal. Данные инструменты выбраны в силу своей доступности и простоты использования, так как основное внимание должно быть сосредоточено на вычислительном эксперименте, а не на инструменте моделирования. К тому же, используя эти инструменты, не имеющие ярко выраженной профессиональной математической направленности, можно получить приемлемую точность вычисления и провести вычислительный эксперимент с высокой надежностью. Задачи данного исследования состоят в том, чтобы выяснить, какое из вычислительных средств является более точным и эффективным для вычисления числа Пи. Необходимо сравнить их вычислительные возможности: трудоемкость, время расчетов и точность вычислений. Задача состоит в том, чтобы провести вычисления числа Пи с точностью до 10-10 в MS Excel и Free Pascal, найти абсолютные и относительные ошибки вычисления. Для моделирования вычисления числа Пи использовались следующие алгоритмы. Алгоритм вычисления числа Пи с помощью метода Грегори–Лейбница. В 1671 году Джеймс Грегори установил:
Результат позволил Лейбницу получить очень простое выражение для Пи [12]:
Этот результат известен как ряд Грегори–Лейбница (Мадхавы–Лейбница). Однако он сходится очень медленно, что на практике приводит к объемным рутинным вычислениям. Например, необходимо просуммировать около 4 000 членов ряда, чтобы улучшить оценку Архимеда. При реализации этого алгоритма на компьютере n будет принимать довольно большие значения для достижения необходимой точности [13]. Листинг программы вычисления числа Пи методом Грегори–Лейбница: Program GregoryLeybnic; var n,i:longint; S:real; z:integer; begin write('Введите число слагаемых: '); readln(n); S:=4; z:=-1; For i:=1 to n do begin S:=S+z*4/(2*i+1); z:=-z; end; writeln('pi=',S:12:10); ReadLn; end. MS Excel (2007) позволяет работать с 500 000 ячеек в столбце. Это число примем как максимальный номер слагаемого. Результаты вычисления Пи методом Грегори–Лейбница приведены в табли- це 1. Таблица 1 Вычисление числа Пи методом Грегори–Лейбница Table 1 Calculation of the number Pi by Gregory-Leibniz method
Результаты вычислений в MS Excel и Free Pascal совпадают. Значение π ≈ 3,1415946536 получено при n = 500 000. Абсолютная ошибка составляет 2·10-6, а относительная ничтожно мала (< 0,001 %). Уточнение ряда Мадхавы. Мадхава, уточняя стандартный знакочередующийся гармонический ряд, пришел к выводу, что число Пи имеет следующее представление, которое дает хорошую качественную оценку числа и высокую точность при малом количестве слагаемых:
Листинг программы вычисления числа Пи через ряд Мадхавы: Program Madhava; var n,i:longint; S1:real; z:integer; begin write('Введите число слагаемых:'); readln(n); S1:=1; z:=1; For i:=1 to n do begin S1:=S1-z/((2*i+1)*exp((i)*ln(3))); z:=-z; end; S1:=S1*sqrt(12); writeln(s1:12:10); ReadLn; end. Вычисления в MS Excel и Pascal дают результаты, отраженные в таблице 2. Как видно из результатов вычислительного эксперимента, абсолютная ошибка равна нулю (при точности 10-10) уже на 20-м слагаемом. И обе среды моделирования, и MS Excel, и Pascal, это подтверждают, так как данные различаются незначительно. Но при аппроксимации числа Пи методом Мадхавы среда Free Pascal эффективнее, так как дает более точные значения на самых первых итерациях, используя всего лишь несколько первых слагаемых. Таблица 2 Вычисление числа Пи методом Мадхавы Table 2 Calculation of the number Pi by Madhava method
Ряд Нилаканта. Еще один бесконечный ряд для вычисления числа Пи − ряд Нилаканта. Он более сложный, чем ряд Лейбница, но дает точное значение Пи гораздо быстрее [3–5]:
Листинг программы вычисления числа Пи через ряд Нилаканта: Program Nilacant; var n,i:int64; S1:real; z:integer; begin write('Введите число слагаемых: '); readln(n); S1:=3; z:=1; i:=2; While i<=n do begin S1:=S1+4*z/(i*(i+1)*(i+2)); i:=i+2; z:=-z; end; writeln(s1:12:10); ReadLn; end. Используя данную формулу, достаточно вычислить тысячу первых слагаемых, чтобы получить точное значение Пи (табл. 3).
Как показывают результаты, ряд Нилаканта сходится намного быстрее, чем ряд Лейбница, но медленнее, чем ряд Мадхавы. Формула Эйлера. Формула Л. Эйлера отличается от остальных тем, что вычисляется квадрат числа Пи, а не само число. Выражение для вычисления квадрата числа Пи имеет следующий вид:
Листинг программы вычисления числа Пи через ряд Эйлера: Program Eyler; var n,i:longint; S:real; begin clrscr; write('Введите число слагаемых: '); readln(n); S:=0; For i:=1 to n do S:=S+1/sqr(i); S:=sqrt(6*S); writeln(S:12:10); ReadLn; end. Результаты вычислений приведены в таблице 4. Таблица 4 Вычисление числа Пи по формуле Эйлера Table 4 Calculation of the number Pi by Euler formula
Значение π ≈ 3,1415831043 получено при n = 100 000. Абсолютная ошибка составляет 9·10-6, а относительная ничтожно мала (< 0,001 %). Формула Валлиса. Отличается от аппроксимаций, приведенных выше, тем, что не является рядом, сумма которого сходится к Пи. Это произведение множителей, которые в результате дают число, близкое к точному значению Пи:
Если вынести первый множитель ‒ число 2 и рассматривать данные произведения попарно, то в числителе будет квадрат четных чисел, а в знаменателе квадрат нечетных чисел, меньших на единицу. Листинг программы вычисления числа Пи через формулу Валлиса: Program vallis; var n,i:longint; P:real; begin write('Введите число слагаемых: '); readln(n); P:=2; i:=2; While i<=n do begin P:=P*sqr(i)/((i-1)*(i+1)); i:=i+2; end; writeln(P:12:10); ReadLn; end. Результаты вычислений приведены в таблице 5. Таблица 5 Вычисление числа Пи методом Валлиса Table 5 Calculation of the number Pi by Wallis method
Используя формулу Валлиса, необходимо вычислить произведение 100 000 множителей, чтобы получить в итоге приближенное значение Пи с необходимой точностью. Обсуждение. В ходе исследования проведены практические вычисления, в основе которых лежат ряды и прочие математические выражения, дающие качественную аппроксимацию числа Пи. Точность вычислений варьируется от 10-5 до 10-10 в MS Excel и Free Pascal, найдены абсолютная и относительная ошибки вычисления. Как показывают результаты вычислений и проведенного исследования, самое точное значение с минимальной абсолютной и относительной ошибкой дает ряд Мадхавы. Оказалось достаточным вычислить сумму всего лишь 20 слагаемых, чтобы получить 10 точных знаков в дробной части числа Пи. Причем указанная точность была достигнута за 20 итераций в двух вычислительных средах: MS Excel и Free Pascal (см. табл. 6). Из сводной таблицы видно, что самым долго сходящимся рядом является ряд Грегори–Лейбница. Потребовалось просуммировать полмилли- она слагаемых, чтобы достичь указанной точности и получить относительную ошибку ≤ 10-3. Далее по точности идут формулы Эйлера и Валлиса. Потре- бовалось около 100 000 слагаемых (множителей), чтобы эти выражения хорошо аппроксимировали число Пи. Ряд Нилаканта при суммировании более 1 000 слагаемых дает 9 верных знаков в числе Пи, но уступает ряду Мадхавы, который достигает ука- занной точности всего лишь за 20 слагаемых. В итоге самым быстро сходящимся и точным рядом является алгоритм Мадхавы. Число слагаемых равно всего лишь 20, абсолютная точность 10-10, а относительная ошибка ≤ 10-3. Выводы. В работе проведен сравнительный анализ различных методов вычисления числа Пи. Для решения этой задачи использовались алгоритмы, основанные на сходимости рядов, и другие математические выражения. В результате вычислительного эксперимента решена задача нахождения числа Пи различными методами с точностью до 10 знаков в дробной части. Рассчитаны абсолютная и относительная ошибки. Самым точным и быстрым алгоритмом является ряд Мадхавы (n = 20). Проведен сравнительный анализ различных методов вычисления числа Пи с использованием двух инструментов – MS Excel и Free Pascal. Показано, что язык программирования является более точным и менее затратным средством проведения расчетов по времени вычисления и объему работу. Литература 1. Кымпан Ф. История числа Пи. М.: Наука, 1971. 217 с. 2. Жуков А.В. О числе π. М.: Изд-во МЦНМО, 2013. 32 с. 3. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. М.: Физматлит, 2003. Т. 2. 864 с. 4. How to Calculate Pi. URL: https://www.wikihow.com/Calculate-Pi (дата обращения: 07.02.2018). 5. Как вычислить значение Пи? URL: http://ru.wikihow. com/вычислить-значение-Пи (дата обращения: 07.02.2018). 6. Bailey D., Borwein P., Plouffe S. On the Rapid computation of various polylogarithmic constants. Mathematics of Computation, 1997, vol. 66, no. 218, рp. 903–913. 7. Bailey D., Borwein J. Pi: The next generation a sourcebook on the recent history of Pi and its computation. Springer, 2016, 507 p. 8. Сальников М.М. О точности исчисления числа Пи // Вестн. Пермского ун-та: Сер: Математика. Механика. Информатика. 2009. № 7. С. 148–156. 9. Чепасов В.И., Токарева М.А., Буреш О.В. Вычисление числа Пи методом касательных в длинной арифметике. Оренбург: Изд-во ОГУ, 2011. 119 с. 10. Кормилицына Т.В. Вычислительный эксперимент и компьютерные модели в свободном программном обеспечении // Учебный эксперимент в образовании. 2010. № 1. С. 18–22. 11. Клинаев Ю.В., Терин Д.В. Методы и технологии компьютерных вычислений в математическом моделировании. Саратов: Изд-во СГТУ, 2010. 205 c. 12. Arndt J., Haenel C. Pi. Algorithmen, computer, arithmetik. Springer-Verlag, Berlin Heidelberg, 2001, 280 p. 13. Цветков А.С. Язык программирования Pascal. СПб, 2013. 46 с. |
| Permanent link: http://swsys.ru/index.php?page=article&id=4475&lang=en |
Print version Full issue in PDF (19.46Mb) |
| The article was published in issue no. № 2, 2018 [ pp. 409-413 ] |
Back to the list of articles

 (1)
(1) (2)
(2)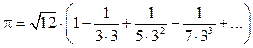 . (3)
. (3)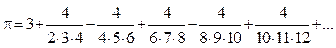 (4)
(4)
 . (5)
. (5)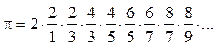 (6)
(6)
