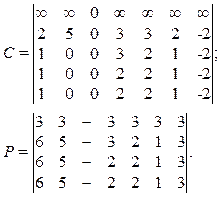Графовые модели широко используются при анализе и синтезе систем сложной структуры, особенно сильно связанных. Программные средства решения данных задач, а также методы визуали- зации свойств графовых структур широко применяются как в прикладных пакетах общего назначения, так и в специализированных системах, например, Intelligent Graph Visualizer, Visual Graph, WEGA и др.
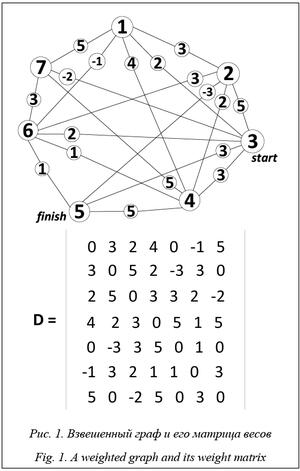 Одной из наиболее распространенных задач на графовых моделях является построение во взвешенном графе маршрута между двумя заданными вершинами, обладающего минимальной стоимостью – суммой весов входящих в него ребер [1–6]. В случае ребер неотрицательного веса для поиска точного решения оптимальным является алгоритм Дейкстры [7]. Однако данный алгоритм нельзя применять в случае наличия ребер отрицательного веса, поскольку в ряде случаев, например, при наличии ребер отрицательного веса, инцидентных стартовой вершине, он не находит даже приближенных решений. Ребра отрицательного веса характерны для экономических задач, в которых вы- полнение отдельных операций может приносить не только прибыль, но и убытки. Пример такой модели дан на рисунке 1.
Одной из наиболее распространенных задач на графовых моделях является построение во взвешенном графе маршрута между двумя заданными вершинами, обладающего минимальной стоимостью – суммой весов входящих в него ребер [1–6]. В случае ребер неотрицательного веса для поиска точного решения оптимальным является алгоритм Дейкстры [7]. Однако данный алгоритм нельзя применять в случае наличия ребер отрицательного веса, поскольку в ряде случаев, например, при наличии ребер отрицательного веса, инцидентных стартовой вершине, он не находит даже приближенных решений. Ребра отрицательного веса характерны для экономических задач, в которых вы- полнение отдельных операций может приносить не только прибыль, но и убытки. Пример такой модели дан на рисунке 1.
Рекомендуемый для решения этой задачи алгоритм Беллмана–Форда, как показывает анализ, даже при самой глубокой модификации гарантирует получение только приближенных решений. Поскольку точное определение минимального пути в графах с ребрами отрицательного веса является актуальной задачей в целом ряде областей, особенно в экономике, в работе рассмотрен алгоритм, гарантированно дающий искомое решение. Его применение может устранить данный существенный пробел в современных программных графовых системах.
Основная проблема графов с отрицательными весами ребер – так называемые отрицательные циклы, в которых сумма весов ребер отрицательна. Исследование данных циклов представляет собой отдельную задачу, для решения которой применяется алгоритм Флойда–Уоршелла [8, 9]. Исследованию их в динамических графах посвящена рабо- та [10].
Поскольку каждый проход по такому циклу уменьшает общую стоимость всего маршрута, в общем случае путь с минимальной стоимостью между заданными вершинами не существует, так как за счет повторения отрицательного цикла ее можно сделать сколь угодно малой. Отрицательные циклы появляются даже при наличии в графе одного ребра с отрицательным весом. Поскольку в реальных системах циклы в маршрутах недопустимы, в этом случае на них налагается дополнительное требование отсутствия циклов – ацикличность.
Существующие подходы к решению задачи. Базовый алгоритм Беллмана–Форда
Исходными данными задачи являются следующие структуры данных:
- взвешенный граф G, заданный тройкой структур: множеством вершин V = {vi} = {v1, …, vn}, множеством ребер Х = {хj} = {х1, …, хm}, матрицей с неотрицательными весами ребер D = {хik} (i =0, …, n–1; k = 0, …, n–1);
- номера start и finish начальной и конечной вершин пути.
В процессе работы алгоритма Беллмана–Форда строятся две вспомогательные структуры:
- матрица стоимостей маршрутов С размерностью n×n, в которой строки с номерами s = 0, …, n–1 соответствуют длинам сsi кратчайших путей из начальной вершины start в вершину vi (номер ее i соответствует номеру столбца матрицы);
- матрица P размерностью (n – 1) × n, в которой для строк с номерами s = 1, 2 ,…, n – 1 в элемент рsi заносится номер s-й по счету вершины в кратчайшем пути в вершину с номером i.
Далее приведен базовый вариант метода.
Шаг 1. Задание начальной строки с номером s = 0 в матрице С, соответствующей путям длины 0. В ней при с0 start = 0 для всех остальных столбцов (i ¹ start) с0i = +∞. Строки с номером 0 в матрице Р нет.
Шаг 2. Расчет строк s = 1, …, n – 1 в матрицах C и Р. Для каждой очередной строки s в С для элемента с[s, i] вначале полагаем, что длина кратчайшего пути длины s такая же, как и найденного ранее пути длины (s – 1), предыдущая вершина – сама вершина i: с[s, i]: = с[s – 1, i]; р[s, i]: = i. Затем путем перебора значений во всех столбцах (t = 1, …, n–1, t ¹ i) предыдущей строки (s – 1) и весов ребер dti производится поиск самого короткого пути длины s из start в i. При их наличии вносятся следующие изменения в матрицы С и Р: если (с(s -1) t + + dti < с si), то с si := с(s-1) t + dti; p si: = t}.
Шаг 3. Определение минимальной стоимости пути Min_cost и числа ребер r в нем по следующему правилу. В строках s столбца finish матрицы С выбираем наименьшее значение. Если таких строк несколько, берем наименьшее значение s. При этом Min_cost: = с s finish; r: = s.
Шаг 4. Определение минимального пути. Начало и конец: Path[1]: = start; Path[r + 1]: = finish. Промежуточные вершины определяются в цикле по номерам строк s = r, …, 2: Path[s]: = = р(s +1)(Path[s +1]).
Применение алгоритма Беллмана–Форда при наличии ребер с отрицательным весом
Для гарантированного построения в графе всех содержательных ациклических минимальных путей обычно в литературе рекомендуется внешний цикл на шаге 2 по расчету строк в матрице C и формированию матрицы Р выполнить (n–1) раз, поскольку самый длинный путь без циклов не может содержать более (n–1) ребер. Однако данные способы предотвращения отрицательных циклов путем наложения общих ограничений (уменьшение длины минимального пути до какой-либо вершины на итерации с номером n, контроль длины таких путей) малоэффективны. Рассмотрим возможные модификации алгоритма, гарантированно обеспечивающие определение ациклического пути.
Первая модификация алгоритма Беллмана–Форда (шаги 3 и 4) – отбрасывание маршрутов с циклами. После выполнения (n – 1) раз внешнего цикла на шаге 2 в столбце, соответствующем конечной вершине finish, необходим дополнитель- ный анализ. Поскольку с увеличением длины путей s стоимости их Min_costf не возрастают, надо последовательно рассмотреть все множество полученных путей {Pathf(n-1), Pathf (n-2), …} в порядке убывания их длин и удалять те их них, которые содержат циклы (их можно обнаружить по повторяющимся вершинам). Первый из оставшихся путей и будет задавать найденный путь минимальной стоимости.
При такой модификации изменяется выполнение только шагов 3 и 4 базового алгоритма.
Вторая модификация алгоритма Беллмана–Форда (шаг 2) – предотвращение появления циклов. Первая модификация предусматривает на шагах 3 и 4 специальную процедуру анализа уже построенных по обычному алгоритму минимальных путей. В общем случае при ее использовании решение может быть приближенным по следующей причине – маршруты с отрицательными циклами могут блокировать построение несколько более длинных ациклических путей на шаге 2. Существенным недостатком данной модификации является генерация излишнего числа строк в матрицах С и Р.
В среднем лучшие результаты дает предотвращение появления отрицательных циклов уже на шаге 2 – при построении матриц С и Р. Рассмотрим данную модификацию более подробно.
Поскольку теоретически циклы могут появиться уже при длине маршрутов s = 2 у начальной вершины start, в строке 2 необходима проверка на цикл только в столбце t = start, а начиная со строки s = 3 в общем случае проверять необходимо все столбцы. Для этого выполнение шага 2 нужно модифицировать следующим образом.
Как и в основном алгоритме, вначале для каждого столбца j производится инициализация элементов матриц: с[s, i]: = с[s – 1, i]; р[s, i]: = i. Затем осуществляется перебор значений во всех столбцах t = 1, …, n – 1 предыдущей строки с номером (s – 1) и соответствующих весов ребер dst, при котором определяются все варианты построения более коротких путей длины s из вершины start в i, упорядочиваемых по возрастанию получаемых значений стоимостей маршрутов.
Если таких вариантов нет, то обработка вершины с номером i прекращается и осуществляется переход к обработке (i + 1). Когда они есть, то начиная с самого малого значения их стоимости производится дополнительная проверка для суммы с(s-1)t + dit; проверяется включение вершины i в оптимальный путь длины (s – 1) для столбца t, соответствующий стоимости с(s-1)t. Если такого включения нет, то данный вариант является оптимальным и производятся обычные изменения в матрицах С и Р: с si:= с(s-1) t + dti; p si:= t. Возможно, что будут отброшены все варианты улучшения стоимости сsi. Обычно процесс построения матриц С и Р завершается не после расчета в них строк с предельным но- мером s = (n – 1), а при их стабилизации, когда текущая строка повторяет предыдущую.
Преимуществом данной модификации перед первой является сокращенный размер матриц С и Р, а также то, что в среднем ее результаты лучше. Однако в общем случае данная модификация не гарантирует получение абсолютно оптимального решения.
Рассмотрим применение второй модификации алгоритма к взвешенному графу, для которого общий вид и матрица весов представлены на рисун- ке 1. Начальная и конечная вершины: start = 3, finish = 5.
Результирующие матрицы С и Р, полученные после стабилизации их строк 3 и 4, имеют следующий вид:
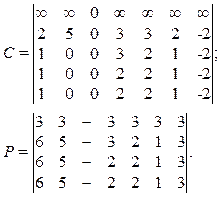
Из матриц С и Р следует, что найденный минимальный путь (3–2–5) имеет стоимость 2. Однако он является приближенным, поскольку абсолютно оптимальным является путь (3–7–6–1–2–5), имеющий стоимость 0.
Таким образом, при наличии в графе ребер отрицательного веса модификации алгоритма Бел- лмана–Форда позволяют в общем случае только приближенно найти минимальный ациклический путь.
Точное решение задачи с использованием метода ветвей и границ
Основная причина потери точных решений при использовании алгоритма Беллмана–Форда в том, что предложенный в нем (как и в методе Дейкстры) вариант применения принципа динамического программирования основан на использовании монотонного возрастания стоимости пути при его продлении, при котором в него добавляется очередное ребро. При наличии ребер отрицательного веса данный принцип нарушается, поскольку добавление ребра с отрицательным весом не увеличивает, а уменьшает суммарный вес пути. Поэтому при точном решении задачи на графах с ребрами отрицательного веса соответствующие модификации данного метода могут быть использованы только для нахождения достаточно близких начальных приближений.
Для точного решения задачи на графах с ребрами отрицательного веса предложено использовать общий метод ветвей и границ, который эффек- тивно применяется в теории графов, например, для решения задачи коммивояжера [11].
Алгоритм поиска минимального ациклического пути в графах, имеющих ребра отрицательного веса, назван алгоритмом исчерпывания вершин, поскольку в нем принцип динамического программирования основан на последовательном решении самоподобных задач построения удлиненного пути с контролем его ацикличности и получаемой возможной минимальной стоимости с учетом ее возможного уменьшения при удлинении пути. Поскольку требование ацикличности рассматриваемых путей сочетается с перебором всех вариантов решения, способных дать оптимальный путь, такой метод позволяет гарантированно найти искомое глобально минимальное ациклическое решение, то есть искомое точное решение задачи. Только учет возможного уменьшения стоимости пути при его продолжении позволяет корректно применить принцип динамического программирования для построения точного решения. В случае отсутствия начального приближения вначале минимальную стоимость пути надо принимать бесконечной, но при этом во вспомогательной структуре будет генерироваться максимальное число узлов. Для сокращения количества анализируемых вариантов в алгоритме можно применять достаточно близкое к точному приближенное решение задачи, которое, в частности, можно определить с использованием второй модификации алгоритма Беллмана–Форда.
Поскольку в предлагаемом методе так же, как и по алгоритму Беллмана–Форда, минимальный путь определяется вначале в обратном порядке, в процессе вычислений данный порядок сохраняется, а реверсирование выполняется однократно – при завершении расчетов.
Алгоритм исчерпывания вершин поиска минимального ациклического пути во взвешенном графе, содержащем ребра отрицательного веса
Исходные и выходные данные алгоритма – те же. Нумерация элементов массивов – с 0.
Вспомогательные структуры:
1) текущая минимальная стоимость minCost ациклического пути из начальной вершины start в конечную вершину finish;
2) список вершин в обратной записи данного пути way [];
3) дерево ациклического перебора, реализованное в виде иерархически послойно связанных между собой однонаправленных списков, в которых узлы имеют структуру Node, включающую следующие элементы:
parent – указатель на предыдущий родительский узел;
vert – номер текущей проходимой вершины графа;
next – указатель на следующий узел в своем слое, в последнем узле слоя next = NULL;
cost – стоимость пути из начальной вершины start в текущую вершину vert;
mv [] – список вершин, которые потенциально могут быть добавлены к уже построенному участку пути при его продолжении;
me [3][] – список ребер отрицательного веса, которые потенциально могут быть включены в продолжение уже построенного участка пути и уменьшить его стоимость.
Также в общую структуру дерева входят следующие указатели:
pPrev – на начало (его начальный узел) предыдущего слоя;
pCur, pCurCur – на начало (начальный узел) и текущий узел текущего слоя;
pNew, pNewCur – на начало (начальный узел) и текущий узел нового (формируемого) слоя;
pВuf – на буферный узел.
Чтобы унифицировать обработку всех слоев, в том числе пустого, предложено каждый слой заканчивать пустым узлом, который не обозначает никакую вершину графа. В нем значение vert = –1.
В общем случае граф может быть несвязным и в нем не существует путей из начальной вершины start в конечную вершину finish. В этом случае алгоритм должен выдать значение minCost, равное бесконечности. При использовании в качестве начального приближения результатов применения второй модификации метода Беллмана–Форда данное значение будет получено уже из него.
Построение вспомогательной структуры данных осуществляется послойно. Номер текущего слоя означает число вершин в путях, задаваемых его узлами. Процесс продолжается до тех пор, пока не будет получен пустой слой New, то есть на текущем шаге не будет найдено ни одного перспективного продолжения пути. Одной из причин пустоты слоя New может быть и достижение предельного числа вершин n в уже построенных путях.
Для упрощения построения, обхода и финального удаления требуемых узлов дерева предложено организовать его структуру в виде иерархически послойно связанных между собой однонаправленных списков, каждый их которых всегда заканчивается пустым узлом. При порождении очередного узла из вышележащего родительского списки вершин и ребер отрицательного веса переносятся в дочерний узел с удалением из них вершины дочернего узла и всех ребер отрицательного веса, инцидентных ей.
Каждый раз при прохождении конечной вершины стоимость вновь построенного пути срав- нивается с текущим значением minCost. Если построен более короткий путь, то его данные заносятся в minCost и way[]. Иначе данный путь пропускается без выполнения каких-либо действий.
Алгоритм включает следующие шаги.
Шаг 1. Предварительные действия.
1.1. Определение minCost и обратного пути way[] при помощи второй модификация Беллмана–Форда. Если minCost = ¥, то выход из алгоритма с данным значением. Иначе – продолжение расчетов.
1.2. Инициализация начального списка вершин V[n – 1], в который включаются все вершины, кроме start.
1.3. Инициализация начального списка ребер отрицательного веса E[3][][] = {(dij, i, j)}.
1.4. Удаление из списка ребер E[3][][] всех ребер, инцидентных начальной вершине start.
1.5. Сортировка списка ребер E[3][][] по возрастанию весов dij.
1.6. Инициализация указателей на текущий, предыдущий слои, а также буферный узел:
Node pCur = null, pPrev = null, pВuf = null.
1.7. Инициализация первого узла слоя New для вершины start со значениями parent = pCur и next = pCur, его доопределение:
Node pNew = new Node(pCur, pCur);
pNew.vert = start; pNew.cost = 0;
V[n – 1] ® pNew.mv; E[3][][] ® pNew.me.
1.8. Инициализация завершающего (пустого) узла NewCur слоя New со значениями parent = pCur, next = pCur и переопределение next для первого узла слоя New:
Node pNewCur = new Node(pCur, pCur);
pNew.next = pNewCur.
1.9. Инициализация номера слоя: numLevel = 0.
Шаг 2. Последовательная обработка слоев.
Непустота очередного слоя New выясняется проверкой условия пустоты его первого узла: pNew.vert != –1.
При его выполнении производятся следующие действия.
2.1. Предварительные действия в обрабатываемом слое:
numLevel++; //Наращивание номера слоя
pPrev = pCur; pCur = pNew; // Переопределение указателей pPrev и pCur
pNew = new Node(pCur, pCur); //Инициализация первого узла слоя New
pCurCur = pCur; pNewCur = pNew; //Задание указателей на текущие узлы слоев Cur и New.
2.2. Последовательная обработка узлов в обрабатываемом слое pCur.
Вначале производится проверка непустоты текущего узла pCurCur по условию pCurCur.vert ! = = –1.
При его выполнении производятся следующие действия.
2.2.1. Определение длины списка ребер отрицательного веса neg.
2.2.2. Расчет максимально возможного числа корректирующих ребер ncor:
ncor = neg; if (ncor > n – numLevel) ncor = = n – numLevel.
2.2.3. Расчет максимально возможного умень- шения стоимости пути Costcor:
Costcor = 0; for (i = 0; i < ncor – 1; i++) Costcor = = pCurCur.me[i].d.
2.2.4. Перебор вершин с номерами i из списка pCurCur.mv, анализ возможных продолжений пути из вершины v.
vp = pCurCur.mv[i]; cost_pr = pCurCur.cost + D[v][vp]; //Определение стоимости продолженного пути if (vp == finish) //Проверка, совпадает ли вершина vp с finish
{if (cost_pr< minCost)// 2.2.4.1. Найден более короткий
путь
{minCost = cost_pr;//Обновление minCost t
way[] = null; finish ® way[]; pВuf = pCurCur;
//Обновление обратного пути way[]
while(pВuf.vert ! = start){pВuf.vert ® way[];
pВuf = pВuf.parent;}
start ® way[];
}
else // 2.2.4.2.Вершина vp не совпадает с finish,
проверка перспективности продолжения по vp
if ((D[v][vp]! =.0) && (cost_pr + Costcor < minCost))
{//Построение очередного узла путем заполнения
последнего пустого в новом слое
pNewCur.vertex = vp; pNewCur.cost = cost_pr;
pCurCur. mv [] ® pNewCur.mv [] ;
Удаление вершины vp из списка pNewCur.mv [];
pCurCur.me[] ® pNewCur.me[] ;
Удаление из списка ребер pNewCur.me [] всех ребер,
которые инцидентны вершине vp
//Инициализации очередного пустого узла в слое
New и смена ссылки next в прежнем
pBuf = new Node(pCurCur, pCur);
pNewCur.next = pBuf; pNewCur = pBuf;
}
}//Завершение обработки очередного узла pCurCur
слоя Cur
pCurCur = pCurCur.next// Переход к обработке
следующего узла текущего слоя
}//Завершение обработки очередного слоя
Шаг 3. Реверсирование порядка вершин в найденном минимальном пути way[].
lw = length(way[];
В цикле по i от 0 до lw/2 – 1 выполняются
пересылки через буфер buf:
{buf = way[i]; way[i] = way[lw – 1 – i];
way[lw – 1 – i] = buf;};
Шаг 4. Освобождение памяти – удаление узлов во всех слоях, начиная с узла pNew.
Завершение работы алгоритма.
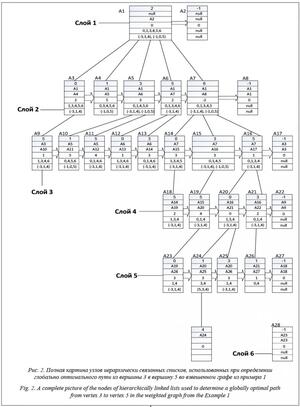
При применении алгоритма к графу из примера при start = 3, finish = 5 (при нумерации элементов массивов с нуля: start = 2, finish = 4) в итоге получаем дерево, представленное на рисунке 2. Адреса узлов обозначены условно их номерами в порядке порождения с добавлением А. В нем в жирной рамке показан абсолютно оптимальный путь (2–6–5–0–1–4) стоимости 0, который порождается после обработки узла А24. При переходе к нумерации вершин от 1 до 7 получим минимальный путь из вершины 3 в вершину 5 вида way[]=(3–7–6–1–2–5).
Поскольку в алгоритме из всего множества возможных путей отбрасываются только те частичные пути, на которых не может быть улучшена текущая оценка стоимости пути, справедлива следующая теорема.
Теорема. Предложенный алгоритм исчерпыва- ния вершин позволяет всегда найти во взвешенном графе, в котором есть ребра отрицательного веса, точное решение (глобальный минимум) при поиске минимального ациклического пути.
В этом состоит принципиальное отличие предложенного алгоритма от применяемых для этой цели других алгоритмов решения рассмотренной задачи, дающих гарантированно только приближенные решения.
Заключение
Применяемое в алгоритме условие отсечения неперспективных частичных путей имеет сравнительно простой вид и не требует выполнения сложных расчетов. В то же время его применение позволяет отбрасывать большое количество неперспективных продолжений рассматриваемых путей.
Алгоритм сформулирован для случая практической реализации его вспомогательной структуры в виде иерархически связанных однонаправленных списков. Это значительно упрощает его програм- мную реализацию по сравнению с традиционными методами обхода деревьев. Применение его поможет устранить существенный пробел в современных графовых программных системах.
Алгоритм реализован практически на языке программирования С#.
За счет некоторого усложнения алгоритма можно сократить объем необходимой вспомогательной памяти. Для этого надо массивы вершин и ребер в узлах списков не постоянно включать в них, а удалять после того, как слой становится предыдущим и потребность в этих массивах для построения следующих слоев отпадает.
Литература
1. Алексеев В.Е., Таланов В.А. Нахождения кратчайших путей в графе. В кн.: Графы. Модели вычислений. Структуры данных. Н. Новгород: Изд-во Нижегородского гос. ун-та, 2005. 307 с.
2. Галкина В.А. Построение кратчайших путей в ориентированном графе: В кн. Дискретная математика. Комбинаторная оптимизация на графах. М.: Гелиос АРВ, 2003. 232 с.
3. Chen D.Z. Developing algorithms and software for geometric path planning problems. ACM Computing Surveys, 1996, vol. 28, i. 4es, art. 18. DOI:10.1145/242224.242246.
4. Ittai A., Amos F., Goldberg A.V., Werneck R.F. Highway dimension, shortest paths, and provably efficient algorithms. Proc. ACM-SIAM Sympos. on Discrete Algorithms, 2010, pp. 782–793.
5. Ittai A., Daniel D., Goldberg A.V., Werneck R.F. A hub-based labeling algorithm for shortest paths on road networks. Proc. Sympos. on Experimental Algorithms, 2011, pp. 230–241.
6. Ладыженский Ю., Попов Ю. Алгоритм определения кратчайших путей между всеми узлами в графе после сжатия двух узлов // Тр. Донецкого национальн. технич. ун-та: Сер. Вычислительная техника и автоматизация. 2006. Т. 107. С. 68–75.
7. Гданский Н.И. Прикладная дискретная математика. Логика. Графы. Автоматы. Алгоритмы. Кодирование. М.: Вузовская книга, 2011. 508 с.
8. Кормен Т.Х., Лейзерсон Ч.И., Ривест Р.Л., Штайн К. Алгоритмы: построение и анализ = Introduction to Algorithms. М.: Вильямс, 2006. 1296 с.
9. Goldberg A.V. Scaling algorithms for the shortest paths problem. SIAM J. on Computing, 1995, no. 24, vol. 3, pp. 494–504.
10. Chandrachoodan N., Bhattacharyya S. Adaptive negative cycle detection in dynamic graphs. Proc. Intern. Sympos. on Circuits and Systems, 2001, pp. V-163–V-166.
11. Костюк Ю.Л. Эффективная реализация алгоритма решения задачи коммивояжера методом ветвей и границ // Прикладная дискретная математика. 2013. № 2. Т. 20. С. 78–90.