Основным источником внешних воздействий на функционирующие космические аппараты (КА) различного назначения является космический мусор (КМ) [1, 2], который образуется вследствие техногенного засорения околоземного космического пространства. Это особенно характерно для областей низких орбит с высотами до 2 000 км и геостационарных орбит, где существует реальная опасность столкновения космических объектов с КА.
В настоящее время на околоземных орбитах функционируют также КА с радиоактивными материалами на борту [3]. Естественно, столкновения таких аппаратов с другими космическими объектами должны быть полностью исключены, например, посредством увода аппарата на другую, безопасную, орбиту. Для реализации этого необходима достоверная информация, предупреждающая о времени и последствиях возможного столкновения. Выработка такой информации составляет решение задачи своевременного и достоверного прогнозирования как возможных столкновений, так и их последствий.
Рассматривают два типа последствий столкно- вений: некатастрофические и катастрофические. Некатастрофические не приводят к разрушению КА, но характеристики качества функциони- рования аппарата могут ухудшиться. Степень ухудшения требуется оценить. Катастрофические столкновения приводят к разрушению аппарата и к прекращению решения установленных для него задач.
Условия возможных столкновений космических объектов многообразны, формализовать их в настоящее время невозможно. Следует отметить, что в «Центре контроля космического пространства» создан и поддерживается каталог по обнаруживаемым космическим объектам. По его данным определяются временные интервалы опасных сближений и прогнозируются столкновения любых пар космических объектов. Таким образом, имеется достаточно подробная информация по сближению объектов и предупреждению возможных столкновений, в том числе по предупреждению возможных опасных сближений заданной группы космических объектов с каждым КА.
Однако для получения исходной информации от соответствующих средств контроля космического пространства и выработки информации о возможных столкновениях космических объектов может потребоваться достаточно большое время, а в связи с опасным загрязнением околоземного пространства требуется расширение каталога – включение в него малоразмерных объектов КМ [4]. Последнее является актуальной сложной проблемой, решение которой зависит от точности измерения координат положения в околоземном пространстве, от количества объектов в пространстве, от точности отождествления измерений с истинными «своими» объектами и от определения орбит их движения при априорной неопределенности относительно возникновения объектов и траекторий их движения, а также от точности прогнозирования орбитальных параметров объектов. Итак, как результат, требуется достаточно много времени на накопление измерений для достоверной каталогизации.
Это обстоятельство может привести к невы- полнению требования по своевременному фор- мированию и выдаче достоверной информации, предупреждающей о некатастрофических и катастрофических возможных столкновениях КА с кос- мическими объектами КМ.
Одним из возможных путей формирования достоверной информации для предупреждения может быть оснащение КА оптико-электронными системами (ОЭС) обнаружения космических объектов [5], движущихся по опасным траекториям.
Из изложенного следуют важные задачи:
- на борту КА, при условии его оснащения ОЭС, в реальном времени должна вырабатываться информация об обнаруженных опасных космических объектах, о показателе – характеристике опасности каждого из них для аппаратов, возможно, подвергающихся некатастрофическому или катастрофическому столкновению с космическим объектом, о параметрах траекторий движения опасных космических объектов и времени возможного столкновения;
- в каждый текущий момент времени КА может находиться в состоянии либо штатного режима функционирования (аппарат функционирует в условиях отсутствия сближения и столкновения с другими космическими объектами), либо предопасного нештатного режима (аппарат функционирует в условиях некатастрофических столкновений с другими космическими объектами), либо опасного нештатного режима функционирования в связи с возникшей опасностью катастрофического столкновения с другими космическими объектами; отсюда возникает необходимость решения задачи прогнозирования текущего состояния аппарата.
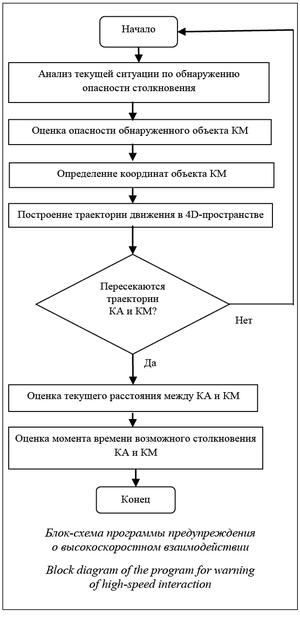 Реализация установленных задач, естественно, должна осуществляться автоматически в реальном времени с помощью бортовой ЭВМ, что, в свою очередь, составляет актуальную научно-техниче- скую проблему. Для ее решения в [6] разработан комплекс ключевых алгоритмов и программ на языке MATLAB, в состав которого необходимо включить программы и алгоритмы выработки информации предупреждения: программы и алгоритмы оценки опасности обнаруженного ОЭС объекта КМ, перевода координат объекта из сферической системы координат ОЭС в инерциальную с началом в центре Земли и сглаживание их как выборки измерений в инерциальной системе для последующего построения эллипса-орбиты движения объекта, оценки текущего расстояния между КА и обнаруженным объектом КМ и алгоритм и программу оценки момента времени возможного столкновения объекта с аппаратом. На рисунке приведена структура дополнительно названных алгоритмов и программ.
Реализация установленных задач, естественно, должна осуществляться автоматически в реальном времени с помощью бортовой ЭВМ, что, в свою очередь, составляет актуальную научно-техниче- скую проблему. Для ее решения в [6] разработан комплекс ключевых алгоритмов и программ на языке MATLAB, в состав которого необходимо включить программы и алгоритмы выработки информации предупреждения: программы и алгоритмы оценки опасности обнаруженного ОЭС объекта КМ, перевода координат объекта из сферической системы координат ОЭС в инерциальную с началом в центре Земли и сглаживание их как выборки измерений в инерциальной системе для последующего построения эллипса-орбиты движения объекта, оценки текущего расстояния между КА и обнаруженным объектом КМ и алгоритм и программу оценки момента времени возможного столкновения объекта с аппаратом. На рисунке приведена структура дополнительно названных алгоритмов и программ.
Структура алгоритма и программа оценки опасности обнаруженного ОЭС объекта КМ
Согласно введенному выше определению опасности объекта, для ее оценки требуется знание диа- метра локальной поверхности КА, возможно, подвергающегося некатастрофическому или катастрофическому неупругому удару объектом КМ [2]. ОЭС КА такую величину не измеряет. ОЭС может измерить в «своей» сферической системе координат θ – угол места, φ – азимут, а также мощность и спектральную плотность силы излучения объектом КМ. Затем для вычисления локальной поверхности КА воспользуемся формулами вычисления максимальной дальности «ОЭС – объект КМ»:
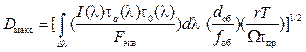 ,(1)
,(1)
 (2)
(2)
где I(l)ta(l) – спектральная плотность силы излучения на входе ОЭС от обнаруженного объекта при коэффициенте пропускания космического пространства ta(l) = 1; t0(l) – коэффициент пропускания ОЭС; Fэкв – эквивалентная мощность шумов ОЭС; dоб/fоб – относительное отверстие объектива ОЭС; dоб – диаметр входного отверстия ОЭС; T – время просмотра угла обзора; r – число элементов поля зрения; W – угол обзора космической обстановки; tпр – постоянная времени ОЭС; Nко, Nш – мощности излучений от объекта и фона с шумом ОЭС (в космосе фон отсутствует, поэтому Nш обозначает только собственный шум ОЭС); sN(Dl) – среднеквадратическое значение шумов чувствительного элемента ОЭС в полосе частот Dl; Sко, Sоэп – площади объекта и входного зрачка ОЭС соответственно; s(l) – спектральная чувствительность ОЭС.
Отметим, что ОЭС представляет собой линейный фильтр безынерционный, Fэкв вычисляется в текущих условиях функционирования ОЭС при закрытом объективе и, естественно, является реализацией случайной величины, значения характеристик (t0, dоб/fоб, Т, W, tпр, r) устанавливаются априори для конкретного ОЭС и по текущему изображению.
По формулам (1) и (2) при измеренных ОЭС величинах I(l) и Nко – спектральной плотности и мощности излучения обнаруженного объекта – можно вычислить Sко – величину излучающей площади объекта КМ.
Для вычисления площади Sко можно воспользоваться также выражением  , где
, где 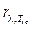 – спектральная интенсивность плотности излучения объекта КМ, зависящая при данной температуре от длины волны, Tко = 273+227; IDl – из- меряемая сила излучения объекта на выходе при- бора ОЭС [6].
– спектральная интенсивность плотности излучения объекта КМ, зависящая при данной температуре от длины волны, Tко = 273+227; IDl – из- меряемая сила излучения объекта на выходе при- бора ОЭС [6].
Но эта величина случайная. Поэтому для оценки опасности столкновения аппарата с обнаруженным объектом воспользуемся оценкой матема- тического ожидания 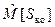 (по выборке измерений площади излучения объекта, формируемой на отрезке времени сопровождения обнаруженного объекта ОЭС) и вычислим максимальный и минимальный диаметры этой площади по 2D-изображениям объекта, формируемым ОЭС.
(по выборке измерений площади излучения объекта, формируемой на отрезке времени сопровождения обнаруженного объекта ОЭС) и вычислим максимальный и минимальный диаметры этой площади по 2D-изображениям объекта, формируемым ОЭС.
Затем допустим, что объект КМ при столкновении «наносит аппарату неупругий удар» площадью с известными максимальным и минимальным диаметрами. Допустим также известной массу объекта КМ. В результате по полученным диаметрам и массе объекта устанавливается характеристика удара [1, 2]: некатастрофический или катастрофический и соответствующие последствия по возможному переходу КА из состояния штатного функционирования в нештатное.
Итак, структура алгоритма оценки опасности обнаруженного ОЭС объекта КМ представляется последовательностью операций вычисления Sко по формулам (1) и (2), вычисления оценки 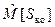 , вычисления максимального и минимального диаметров площади 2D-изображения обнаруженного объекта КМ, вычисления характеристики его опасности для КА и распознавания текущего состояния аппарата. Программная реализация оценки опасности обнаруженного ОЭС объекта космического мусора:
, вычисления максимального и минимального диаметров площади 2D-изображения обнаруженного объекта КМ, вычисления характеристики его опасности для КА и распознавания текущего состояния аппарата. Программная реализация оценки опасности обнаруженного ОЭС объекта космического мусора:
syms l;
dl = diff(l);
Dmax = (int( (((I*ra*r0)/F) * dl * (d / f) * (rT / (o * r) )) , n1, n2)) ^ 0.5;
Формулы и процедуры связи сферической системы координат ОЭС с инерциальной системой координат, принцип сглаживания выборки измерений
Рассматриваются три системы координат.
· Сферическая система, связанная и вращающаяся с КА. В этой системе ОЭС аппарата обнаруживает объекты КМ, измеряет угловые координаты объекта, мощность и спектральную плотность принимаемого от него оптического излучения.
· «Топоцентрическая» прямоугольная система, непосредственно связанная со сферической системой и вращающаяся вместе с ней.
· Инерциальная система координат, в которой вращаются КА и объекты КМ, то есть в которой вращается прямоугольная система координат, связанная с КА. В этой же системе должна вырабатываться и информация, предупреждающая о возможных столкновениях объектов КМ с аппаратом.
Для выработки информации для предупреждения необходимо измеренные ОЭС угловые коорди- наты обнаруживаемых объектов КМ передать из «своей» сферической системы в «свою» топоцентрическую прямоугольную, а затем из нее в инерциальную с учетом вращения прямоугольной вокруг инерциальной. Вращение осуществляется по траектории движения КА (по эллиптической или круговой орбите). Координаты начала прямоугольной системы известны на любой момент времени в инерциальной системе.
Соответствующие преобразования выполняются с использованием известных соотношений аффинных преобразований.
· Из сферической в прямоугольную ОЭС: D, j, q ® x, y, z, где D – дальность; j – азимут; q – угол места обнаруженного ОЭС объекта; x, y, z – координаты объекта в прямоугольной системе.
Формулы перехода записываются в виде
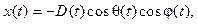
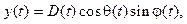

Координаты D, j, q являются случайными функциями времени. Скорости изменения координат объекта вычисляются как производные по времени от этих соотношений.
· Из прямоугольной в инерциальную с учетом вращения прямоугольной системы относительно начала координат инерциальной системы: x(t), y(t), z(t) ® X(t), Y(t), Z(t), где X(t), Y(t), Z(t) – координаты обнаруживаемого ОЭС объекта в инерциальной системе (случайные).
Формулы перехода к координатам X(t), Y(t), Z(t) записываются в виде
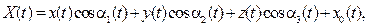


где ai, bi, gi, i = 1, 2, 3 – направляющие косинусы, связанные с эйлеровыми углами, которые определяются между положительными направлениями осей систем координат; x0(t), y0(t), z0(t) – координаты начала прямоугольной системы в инерциальной системе.
Скорости изменения координат объекта в инерциальной системе вычисляются как производные от выражений для X(t), Y(t), Z(t).
Допустимо считать, что координаты X(t), Y(t), Z(t) определяются в дискретные моменты време- ни tj, j = 1, 2, …, n, на коротком отрезке, то есть в моменты времени измерения сферических координат обнаруживаемого объекта, и составляют выборку.
В силу случайности измерений дальности (D), азимута (j) и угла места (q) обнаруженного ОЭС объекта координаты X(tj), Y(tj), Z(tj), tj, j = 1, 2, …, n, представляют случайные выборки. Такие выборки следует сгладить. Для этого воспользуемся предложенным в [6] адаптивным интерполяционным фильтром при представлении функций времени ис- тинных координат движения объекта полиномами второй степени. На коротком отрезке времени обнаружения ОЭС объекта его эллиптическая траектория движения будет достаточно хорошо аппроксимирована полиномом второй степени.
Приведенные соотношения несложно алгорит- мизировать и реализовать в бортовой ЭВМ КА для последующей выработки информации, предупреждающей о возможном столкновении аппарата с обнаруживаемым объектом КМ. Программная реализация на языке MATLAB:
[x, y, z] = SPH2CART[AZ, EL, D];
X = x*cos(a1) + y*cos(a2) + z*cos(a3) + x0;
Y = x*cos(b1) + y*cos(b2) + z*cos(b3) + y0;
Z = x*cos(y1) + y*cos(y2) + z*cos(y3) + z0.
Структура алгоритма и программа построения эллипса-траектории движения объекта КМ
В основу построения эллипса-траектории движения обнаруживаемого объекта КМ принимается известный метод нахождения элементов орбиты по трем положениям объекта в любые три момента tj, j = 1, 2, …, n, при предварительном вычислении сглаженных орта нормали плоскости орбиты-эллипса и части эллипса, аппроксимируемой гладкой кривой второго порядка на отрезке времени обнаружения объекта. Необходимость вычисления такого орта и части эллипса исходит из случайности выборок измерений координат положения объекта X(tj), Y(tj), Z(tj), а значит, и из случайности направления орта, вычисляемого по любой тройке случайных векторов:

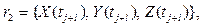

0 £ j + l + k £ n в инерциальной системе.
Алгоритм и программа включают следующие вычислительные операции:
- формирование выборок-троек r1, r2, r3 векторов измеренных координат обнаруженного объекта КМ; их количество равно 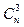 ;
;
- вычисление по r1, r3 каждой тройки r1, r2, r3 орта нормали плоскости орбиты движения объекта КМ по выражению 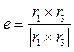 ; при этом конец орта в инерциальной системе координат имеет координаты
; при этом конец орта в инерциальной системе координат имеет координаты 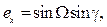
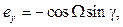
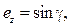 W – восходящий узел (от 0 до 2π), g – наклонение орбиты (от 0 до π); числа W и g полностью определяют положение плоскости орбиты в инерциальной системе;
W – восходящий узел (от 0 до 2π), g – наклонение орбиты (от 0 до π); числа W и g полностью определяют положение плоскости орбиты в инерциальной системе;
- вычисление W и g непосредственным срав- нением значений одноименных координат орта 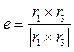 и координат ex, ey, ez;
и координат ex, ey, ez;
- вычисление по выражению эмпирического математического ожидания сглаженных W, g и ко- ординат 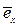 ,
, 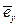 ,
, 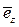 , однозначно определяющих по- ложение орта нормали плоскости орбиты движе- ния обнаруженного объекта КМ;
, однозначно определяющих по- ложение орта нормали плоскости орбиты движе- ния обнаруженного объекта КМ;
- составление уравнения плоскости орбиты движения объекта КМ в виде 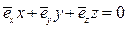 , где
, где 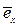 ,
, 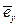 ,
, 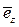 – сглаженные координаты орта плоскости;
– сглаженные координаты орта плоскости;
- составление канонических уравнений прямых, проходящих через две точки: точка-начало инерциальной системы координат (координаты 0, 0, 0) и точка с координатами соответствующего измеренного вектора {X(tj), Y(tj), Z(tj), j = 1, 2, …, n}; уравнения записываются в виде
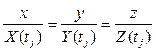 ;
;
- проверка условия принадлежности канонических прямых векторов измерений плоскости орбиты по правилу: если
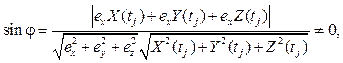
то вектор X(tj), Y(tj), Z(tj) не принадлежит плоскости орбиты, в противном случае принадлежит; j – угол между прямой, содержащей вектор измерений, и плоскостью орбиты;
- выполнение для векторов измерений, не принадлежащих плоскости орбиты (φ≠0), центроаффинного преобразования – вращения вокруг центра инерциальной системы на угол φ (поворот вектора измерений X(tj), Y(tj), Z(tj), j = 1, 2, …, n, до совмещения с плоскостью орбиты) и вычисление их координат в «новых» положениях (положениях на плоскости орбиты);
- формирование 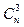 выборок-троек (r1, r2, r3) векторов измерений координат положения объекта в плоскости его орбиты;
выборок-троек (r1, r2, r3) векторов измерений координат положения объекта в плоскости его орбиты;
- аппроксимация квадратичной параболой части орбиты движения объекта КМ, обнаружи- ваемого на отрезке времени измерения векторов независимых координат объекта в плоскости его орбиты; аппроксимация выполняется по каждой координате отдельно (формируются три параболы как функции времени) с использованием метода наименьших модулей как метода, реализующего критерий равномерной сходимости и обеспечивающего наивысшую точность приближения к истинной орбите объекта;
- формирование по сглаженным параболам векторов координат трех различных точек положе- ния объекта (в три момента времени) на плоскости его орбиты;
- нахождение элементов орбиты движения объекта КМ по трем его положениям в плоскости орбиты; для этого используется известный алгоритм;
- определение на построенной орбите координат текущего положения объекта и координат его положения на любой другой момент времени.
Раскроем вычислительную операцию нахожде- ния элементов орбиты. Она представляется следующей последовательностью вычислительных операций:
– вычисление p – параметра эллипса по выражению r2 – p = с1(r1 – p) + с3(r3 – p), где с1 и с3 определяются по формулам r2 ´ r3 = с1(r1 ´ r3) и r2 ´ r1 = = с3(r3 ´ r1);
– вычисление ε – эксцентриситета эллипса по выражению
 ;
;
– вычисление большой (a) и малой (b) полуосей и расстояния от фокуса до центра эллипса:
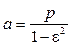
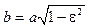
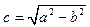 ;
;
– вычисление ортов осей орбитальной системы координат j, k и i из уравнений
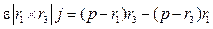 ,
, 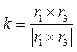
и i = j ´ k; вектор i направлен по оси апсид в плоскости орбиты, вектор j перпендикулярен оси апсид и лежит в плоскости орбиты, вектор k перпендикулярен плоскости орбиты.
По векторам i, j восстанавливается орбитальная система координат, а по известным полуосям однозначно строится в этой системе искомая эллипс-орбита движения объекта КМ.
Структура программы и алгоритма оценки текущего расстояния между КА и обнаруженным объектом КМ
В случае возможного столкновения обнаруженного объекта КМ с КА в инерциальной системе координат текущее расстояние определяется суммой длин двух дуг:
- дуги эллипса движения объекта от точки текущего положения на эллипсе до точки пересечения этим эллипсом плоскости эллипса движения КА (точка пересечения принадлежит линии пересечения плоскостей эллипсов движения объекта КМ и КА);
- дуги эллипса движения КА от точки его текущего положения до точки пересечения эллипсом объекта КМ плоскости эллипса движения КА.
Очевидно, структура программы и алгоритма оценки текущего расстояния между объектом и КА должна включать следующие вычислительные операции:
– определение линии пересечения плоскости эллипса движения объекта КМ с известной плоскостью эллипса движения КА; уравнение линии пересечения плоскостей устанавливается по выражению (линия проходит через начало инерциальной системы координат)
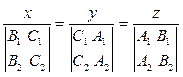 ,
,
где А1, В1, С1, А2, В2, С2 – коэффициенты уравнений плоскостей аппарата и объекта КМ в инерциальной системе координат; уравнение плоскости движения объекта КМ устанавливается из условий ее прохождения через центр Земли и два радиус-вектора со сглаженными координатами 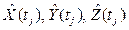 концов, взятых в различные моменты времени tj, j = 1, 2, движения объекта в «своей» плоскости в инерциальной системе; иначе строится уравнение плоскости по трем точкам (0, 0, 0),
концов, взятых в различные моменты времени tj, j = 1, 2, движения объекта в «своей» плоскости в инерциальной системе; иначе строится уравнение плоскости по трем точкам (0, 0, 0), 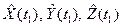 ,
,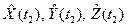 , не лежащим на одной прямой, то есть по выражению
, не лежащим на одной прямой, то есть по выражению
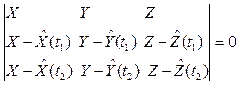 ;
;
- определение координат точки пересечения плоскости эллипса движения КА траекторией движения объекта КМ;
- проверка условия прохождения эллиптической траекторией движения КА через вычисленную точку пересечения;
- вычисление длин дуг траекторий движения объекта КМ и КА от текущих точек их положения до установленной точки пересечения при выполнении условия ее принадлежности траектории движения КА;
- вычисление текущего расстояния между объектом КМ и КА.
Структура программы и алгоритма оценки момента времени возможного столкновения объекта с аппаратом
Устанавливается по формуле вычисления продолжительности перелета обнаруженного объекта КМ по своей эллиптической орбите между двумя точками: точкой его текущего положения и точкой пересечения его траекторией плоскости, в которой движется КА. Соответствующая формула записывается в виде
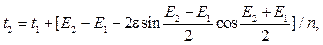
где t2 – момент времени возможного столкновения объекта КМ с КА; t1 – момент времени текущего положения объекта на своей орбите; ε – эксцентри- ситет орбиты объекта; Е1, Е2 – эксцентрические аномалии точки текущего положения объекта КМ и точки пресечения его траекторией плоскости эллипса движения КА; n – средняя угловая скорость движения объекта, 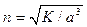 ; a – большая полуось эллипса движения объекта КМ; K – гравитационный параметр.
; a – большая полуось эллипса движения объекта КМ; K – гравитационный параметр.
Заключение
Из изложенного следует необходимость решения важной актуальной проблемы: выработка на борту КА, оснащенного ОЭС, в реальном времени информации об обнаружении опасных космических объектов и характеристике опасности каждого из них для конкретного КА, с прогнозом степени потенциального ущерба столкновения, о параметрах траекторий движения опасных объектов КМ и времени предупреждения о возможном столкновении.
Для решения этой проблемы разработаны комплекс программ на языке MATLAB и алгоритмов обнаружения, распознавания, сопровождения объектов КМ, программы и алгоритмы выработки информации предупреждения: алгоритмы и программа оценки опасности обнаруженного ОЭС объекта КМ, момента времени возможного столкновения объекта с КА и типа последствий столкновения. Работа алгоритмов и программ должна осуществляться автоматически в реальном времени с помощью бортовой ЭВМ.
Исследование выполнено при финансовой поддержке Министерства образования и науки Российской Федерации, проект № 2.1777.2017/4.6.
Литература
1. Райкунова Г.Г. Космический мусор. Кн. 1: Методы наблюдения и модели космического мусора. М.: Физматлит, 2014. 248 с.
2. Райкунова Г.Г. Космический мусор. Кн. 2: Предупреждение образования космического мусора. М.: Физматлит, 2014. 188 с.
3. Brown O., Cottom T. Report on space traffic management assessments, frameworks and recommendations. U.S. Commercial Space Launch Competitiveness, 2016. URL: http://www.spacepolicyonline.com/pages/images/stories/Orbital%20Traffic%20Mgmt% 20report%20from%20SAIC.pdf (дата обращения: 20.07.2017).
4. Stansbery G. Orbital debris research at NASA. Johnson Space Center, Houston, 2010. URL: http://aero.tamu.edu/sites/default/files/faculty/alfriend/S2.2%20Stansbery.pdf (дата обращения: 08.07.2017).
5. Shell J.R. Optimizing orbital debris monitoring with optical telescopes. Advanced Maui and Optical Space Surveillance Technologies Conf., 2010, pp. 427–443.
6. Катулев А.Н., Храмичев А.А., Ягольников С.В. Цифровая автоматическая обработка слабоконтрастных изображений: методы и алгоритмы обнаружения, распознавания и сопровождения динамических объектов. М.: Радиотехника, 2017. 336 с.
7. Криксунов Л.З. Приборы ночного видения. К.: Техника, 1975. 216 с.
References
- Raykunova G.G. Kosmichesky musor. Kn. 1: Metody nablyudeniya i modeli kosmicheskogo musora [Space Debris. Book 1, Space Debris Observation Methods and Models]. Moscow, Fizmatlit Publ., 2014, 248 p.
- Raykunova G.G. Kosmichesky musor. Kn. 2: Preduprezhdenie obrazovaniya kosmicheskogo musora [Space Debris. Book 2, Space Debris Prevention]. Moscow, Fizmatlit Publ., 2014, 188 p.
- Brown O., Cottom T. Report on Space Traffic Management Assessments, Frameworks and Recommendations. 2016. Available at: http://www.spacepolicyonline.com/pages/images/stories/Orbital%20Traffic%20Mgmt%20report%20from%20
SAIC.pdf (accessed July 20, 2017).
- Stansbery G. Orbital Debris Research at NASA. Johnson Space Center, Houston, 2010. Available at: http://aero.tamu.
edu/sites/default/files/faculty/alfriend/S2.2%20Stansbery.pdf (accessed July 8, 2017).
- Shell J.R. Optimizing Orbital Debris Monitoring with Optical Telescopes. Advanced Maui and Optical Space Surveillance Technologies Conf. 2010, pp. 427–443.
- Katulev A.N., Khramichev A.A., Yagolnikov S.V. Tsifrovaya avtomaticheskaya obrabotka slabokontrastnykh izobrazheny: metody i algoritmy obnaruzheniya, raspoznavaniya i soprovozhdeniya dinamicheskikh obektov [Digital Automatic Processing of Low-Contrast Images: Methods and Algorithms for Detection, Recognition and Tracking of Dynamic Objects]. Moscow, Radiotekhnika Publ., 2017, 336 p.
- Kriksunov L.Z. Pribory nochnogo videniya [Night Vision Devices]. Kiev, Tekhnika Publ., 1975, 216 p.




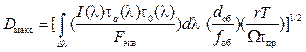 ,(1)
,(1) (2)
(2) , где
, где 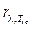 – спектральная интенсивность плотности излучения объекта КМ, зависящая при данной температуре от длины волны, Tко = 273+227; IDl – из- меряемая сила излучения объекта на выходе при- бора ОЭС [6].
– спектральная интенсивность плотности излучения объекта КМ, зависящая при данной температуре от длины волны, Tко = 273+227; IDl – из- меряемая сила излучения объекта на выходе при- бора ОЭС [6].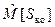 (по выборке измерений площади излучения объекта, формируемой на отрезке времени сопровождения обнаруженного объекта ОЭС) и вычислим максимальный и минимальный диаметры этой площади по 2D-изображениям объекта, формируемым ОЭС.
(по выборке измерений площади излучения объекта, формируемой на отрезке времени сопровождения обнаруженного объекта ОЭС) и вычислим максимальный и минимальный диаметры этой площади по 2D-изображениям объекта, формируемым ОЭС.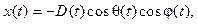
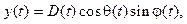

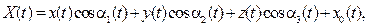



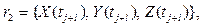

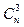 ;
;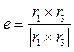 ; при этом конец орта в инерциальной системе координат имеет координаты
; при этом конец орта в инерциальной системе координат имеет координаты 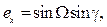
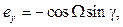
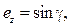 W – восходящий узел (от 0 до 2π), g – наклонение орбиты (от 0 до π); числа W и g полностью определяют положение плоскости орбиты в инерциальной системе;
W – восходящий узел (от 0 до 2π), g – наклонение орбиты (от 0 до π); числа W и g полностью определяют положение плоскости орбиты в инерциальной системе;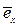 ,
, 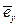 ,
, 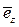 , однозначно определяющих по- ложение орта нормали плоскости орбиты движе- ния обнаруженного объекта КМ;
, однозначно определяющих по- ложение орта нормали плоскости орбиты движе- ния обнаруженного объекта КМ;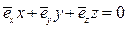 , где
, где 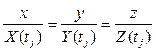 ;
;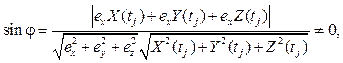
 ;
;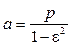
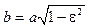
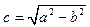 ;
;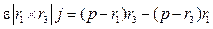 ,
, 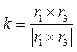
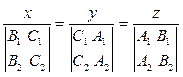 ,
,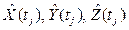 концов, взятых в различные моменты времени tj, j = 1, 2, движения объекта в «своей» плоскости в инерциальной системе; иначе строится уравнение плоскости по трем точкам (0, 0, 0),
концов, взятых в различные моменты времени tj, j = 1, 2, движения объекта в «своей» плоскости в инерциальной системе; иначе строится уравнение плоскости по трем точкам (0, 0, 0), 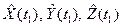 ,
,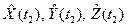 , не лежащим на одной прямой, то есть по выражению
, не лежащим на одной прямой, то есть по выражению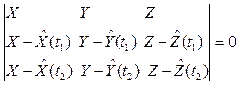 ;
;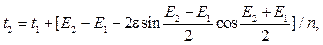
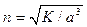 ; a – большая полуось эллипса движения объекта КМ; K – гравитационный параметр.
; a – большая полуось эллипса движения объекта КМ; K – гравитационный параметр.