Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Метод управления пакетом проектов заказов на предприятии оборонно-промышленного комплекса
Аннотация:Статья посвящена решению задачи управления пакетом проектов заказов на предприятии оборонно-промышленного комплекса. Если в процессе реализации крупных проектов показатели освоенного объема и фактических затрат совпадают с плановыми, то при фиксированных целях (относительно планируемого суммарного объема и планируемой продолжительности) необходимость в оперативном управлении отсутствует. Если же в процессе реализации проекта наблюдаются отклонения основных показателей освоенного объема от плановых значений, возникает необходимость оперативного управления. Рассматриваются различные возможные случаи несоответствия основных показателей, и предлагается метод управления процессом выполнения проекта. Ключевая идея, лежащая в основе метода освоенного объема, заключается в следующем: показатели освоенного объема являются характеристиками, на основании исследования которых на ранних стадиях выполнения проекта возможна (иногда достаточно точная) оценка их будущих значений и, следовательно, выработка на их основе своевременных оперативных управляющих воздействий. Предложенные показатели могут описывать проекты, состоящие как из одной, так и из нескольких операций. Если проект состоит из нескольких операций, возникает вопрос о том, как агрегировать показатели подпроектов, операций и т.д. Важную роль при этом играют структура декомпозиции работ (дерево работ, в котором проект последовательно разбивается на более мелкие составляющие) и план контроля затрат – совокупность процедур определения стоимостей элементов структуры декомпозиции работ и правил их агрегирования. Основные преимущества метода заключаются в том, что он оперирует теми же показателями, что и руководитель проекта (который делает это формально или интуитивно), достаточно прост в использовании и, что самое главное, позволяет принимать решения в реальном режиме времени.
Abstract:The article considers the problem of managing an order projects package at a defence contractor. If, the indicators of the absorbed volume and actual costs coincide with the planned ones while implementing large projects, then for fixed purposes (in reference to the planned total volume and planned duration) there is no need for operational management. If the main indicators of the earned value deviate from the planned ones while implementing the project, then there is a need for operational control. The paper considers various possible cases of inconsistency of the main indicators. It also proposes a method for managing the project implementation process. The key idea of the earned volume method consists in the following: the indicators of the earned volume are characteristics that might be a base for developing timely operational control actions at early project stages due to the possibility of estimating their future values (sometimes sufficiently accurate). The proposed indicators can describe projects consist-ing of one or several operations. If the project consists of several operations, then there is a problem of aggregating the indicators of subprojects, operations, etc. A work breakdown structure plays an important role (a tree of works in which the project is consistently divided into smaller parts) and a cost control plan is a set of procedures of determining the values of the work breakdown structure elements and the rules for their aggregation. The main advantages of the method are that it uses the same indicators as the project manager (who does it formally or intuitive-ly), it is easy enough to use and, most importantly, it allows real-time decision making.
| Авторы: Семенов В.Ю. (semenov@mniirs.org) - Московский научно-исследовательский институт радиосвязи (финансовый директор), Москва, Россия, Допира Р.В. (rvdopira@yandex.ru) - НПО РусБИТех, пр-т Калинина, 17, г. Тверь, 170001, Россия (профессор, зав. отделом), г. Тверь, Россия, доктор технических наук, Ягольников Д.В. (yagolnikov_dv@mail.ru) - Военная академия воздушно-космической обороны им. Маршала Советского Союза Г.К. Жукова (преподаватель), Тверь, Россия | |
| Ключевые слова: распределение ресурса, мониторинг, пакет заказов, предприятие опк, управление пакетом проектов |
|
| Keywords: resource distribution, the automated information system, package of orders, defence contractor, project package management |
|
| Количество просмотров: 6280 |
Статья в формате PDF Выпуск в формате PDF (29.80Мб) |
Сложность процессов выполнения проектов предприятия оборонно-промышленного комплекса (ОПК) требует развития экономико-математических методов управления этими процессами. При этом возникает необходимость решения задач распределения ресурсов между несколькими проектами. На этапе планирования каждого проекта определяются ресурсы и время выполнения каждой работы проекта [1]. Планирование осуществляется в условиях неопределенности, что обусловливает риск несвоевременного завершения проектов. При формировании сводного тематического плана предприятия на заданный плановый период необходимо по результатам мониторинга состояния проектов решать задачу определения дополнительных ресурсов на компенсацию рисков и распределения этих ресурсов между проектами. Под ресурсом, подлежащим распределению, будем понимать их суммарный объем, выраженный в стоимостном эквиваленте. Дополнительные ресурсы создаются как страховой фонд для снижения рисков выполнения проектов. Так как директивные сроки завершения проектов в общем случае превышают конец цикла управления, целесообразно заложить в критерий оптимизации степень влияния проектов в заданные сроки. Оптимальное распределение дополнительного ресурса между проектами даже при линейной зависимости выполнения работ проекта от назначаемого ресурса является сложной оптимизационной задачей. Сложность задачи возрастает в условиях стохастичности времени выполнения проектных работ. Выход из такого положения в оперативном управлении пакетом проектов на основе мониторинга процессов выполнения всех проектов. Многие научно-производственные предприятия ОПК для реализации крупных проектов по созданию новых образцов техники применяют современные технологии проектного менеджмента. Однако большинство таких проектов редко завершают в заданные сроки и в размере выделенного бюджета. Это связано с неполнотой и неточностью исходной информации при принятии управленческих решений, с неопределенностью будущих событий, изменчивой внутренней средой и внешним окружением проекта [2, 3]. Планирование и контроль выполнения проекта считаются наиболее важными процессами управления проектами. По данным исследований, часто возникающими при реализации проектов пробле- мами [4, 5] специалисты называют следующие: - изменение целей в ходе выполнения проекта; - недостаток ресурсов, необходимых для успешного выполнения проекта; - неправильная оценка длительности и стоимости выполнения работ; - неточная предварительная оценка возможных проектных рисков; - неэффективная организация контроля и отчетности по проекту; - неполная или недостоверная информация о выполнении работ проекта. В проектном менеджменте основное внимание уделяют длительности, стоимости и качеству выполнения работ проекта. Эти показатели зависят не только от принятых управленческих решений, но и от негативного воздействия наступивших проектных рисков. Подробно процессы управления сроками, стоимостью и качеством в проекте описаны в общепринятых международных стандартах по управлению проектами. Специалисты консалтинговых компаний рекомендуют в ходе выполнения проекта обязательно проводить регулярный аудит принятых допущений и отмечают, что 50 % случаев задержек в проекте – это результат воздействия внутренних рисков и несвоевременно принятых управленческих решений. Недооценка будущих затрат и прямые потери, связанные с ошибочными действиями исполнителей, могут составлять 10–20 % от принятого бюджета проекта. Таким образом, при большом количестве выполняемых проектов у руководства предприятия просто физически не хватает времени на контроль действий по каждому из них, оно не видит общей картины происходящего и испытывает недостаток отчетной информации для принятия управленческих решений, соответствующих реальному состоянию проектов. Анализ существующих в рамках выделенной проблемной области публикаций позволяет сделать следующие выводы: - при планировании проектов рекомендуют создавать резервный фонд в размере 15–20 % от стоимости проекта для ликвидации последствий возможных неблагоприятных событий; - необходимо проводить регулярный контроль выполнения работ проектов для достижения их основных целей и результатов; - для контроля длительности и стоимости выполнения работ проекта обычно применяют метод освоенного объема. В качестве нерешенных задач рассматриваемой проблемной области можно выделить: - необходимость совершенствования существующей методологии проектного менеджмента в части совместного управления длительностью, стоимостью, качеством и рисками проекта; - отсутствие хорошо структурированных и формализованных методик контроля выполнения работ проекта; - необходимость своевременного принятия соответствующих управленческих решений в случае наступления неблагоприятных событий в ходе выполнения проекта. Таким образом, разработка методов контроля выполнения работ проекта для достижения его основных целей и результатов с минимальными издержками является актуальной научно-прикладной задачей, которая до сих пор достаточно полно и удачно не решена. Обеспечение эффективного выполнения проектов требует разработки методов регулярного контроля длительности и стоимости работ в проектах. В основу методического подхода к управлению процессом выполнения проекта положена методика освоенного объема [6], которая предполагает составление полного описания проекта и детального графика его реализации еще на начальной стадии. Это позволяет оценивать фактические данные и контролировать проект с начала и до полного завершения работ. Преимущество этого инструмента в том, что можно получать надежные данные о ходе выполнения проекта уже на стадии его 15–20 %-ного выполнения. Руководитель проекта может использовать эти данные для прогноза затрат, требующихся для завершения всех работ по проекту. Если на ранней стадии выполнения проекта руководитель получает данные по фактической реализации проекта, неприемлемые по ряду показателей, это может послужить для него предупредительным сигналом и позволит предпринять своевременные шаги для предотвращения нежелательных последствий. В качестве основных показателей для описания отдельных операций и проекта в целом будем использовать показатели освоенного объема: C0 – планируемые суммарные затраты на проект; T0 – планируемый срок завершения проекта; c0(t) – планируемая динамика затрат – директивный график; c(t) – фактическая динамика затрат; ce(t) – динамика освоенных затрат; T – фактический срок окончания проекта; C – фактические суммарные затраты на проект. Производными показателями освоенного объема являются Δ0(t) = c0(t) ‒ c(t) – разность между плановыми и фактическими затратами; Δ(t) = = c0(t) ‒ ce(t) – разность между плановыми и освоенными затратами; Δe(t) = c(t) ‒ ce(t) ³ 0 – разность между фактическими и освоенными затратами; α(t) = ce(t) / c0(t) – показатель освоенного объема; β(t) = ce(t) / c(t) – показатель динамики (освоения) затрат. Рассмотрим методику освоенного объема для частного случая линейных интенсивностей, то есть проекта, в котором скорость изменения объема пропорциональна ресурсу: w(l(t)) = k0λ(t), k0 > 0, и количество ресурса l(t) = l0 постоянно во времени. Если u0 – планируемое количество ресурса (затраты в единицу времени), то планируемая динамика затрат имеет вид c0(t) = l0t, а планируемая динамика объема x0(t) = k0l0t. Если X0 – суммарный объем работ по проекту, то планируемая продолжительность проекта T0 = = X0 ¤ (k0l0), а суммарные плановые затраты на проект независимо от интенсивности потребления ресурса C0 = X0 ¤ k0. Применение разработанных методов контроля длительности и стоимости выполнения работ проекта позволяет: - осуществлять регулярный контроль выполняемых предприятием проектов; - выявлять работы проекта, относительно которых были приняты неверные допущения по длительности и стоимости выполнения; - своевременно принимать адекватные управленческие решения, соответствующие реальному состоянию проекта; - снизить негативное воздействие неблагоприятных для проекта событий на достижение его основных целей и результатов; - обеспечить успешное завершение работ проекта в заданные сроки и в размере выделенного бюджета; - накапливать корпоративные знания и практический опыт в управлении проектами. При выполнении любого проекта следует учитывать возможность наступления различных неблагоприятных событий, которые могут существенно повлиять на достижение основных целей и результатов проекта, привести к увеличению его сметной стоимости и несвоевременному завершению. Для ликвидации негативных последствий отклонений при выполнении работ проекта на этапе его планирования создают специальные резервы по ресурсам, времени и стоимости. Обычно на формирование резервного фонда выделяют средства, величина которых может составлять 15–25 % от стоимости проекта. Однако финансовые ресурсы, выделяемые на создание таких фондов, в целом имеют низкую доходность и снижают экономическую эффективность проекта, а объем денежных средств резервного фонда не всегда соответствует величине возможных отклонений в проекте. Для обеспечения эффективного выполнения проектов на основе модели иерархического управления проектами разработаны методы регулярного контроля длительности и стоимости проектных работ. Применение данных методов дает предприятию возможность с минимальными издержками успешно завершать свои проекты в заданные сроки и в размере установленного бюджета. Если в процессе реализации показатели освоенного объема и фактических затрат совпадают с пла- новыми, то при фиксированных целях (относи- тельно планируемого суммарного объема и планируемой продолжительности) нет необходимости в оперативном управлении. Если же в процессе реализации проекта наблюдаются отклонения основных показателей освоенного объема от плановых значений, возникает необходимость оперативного управления. Рассмотрим возможные случаи. Предположим, что l = l0, но фактическая интенсивность k использования ресурса l0 оказалась меньше планируемой: k £ k0. Тогда динамика фактических затрат совпадает с плановой (при T £ T0): c(t) = l0t = c0(t), а значение освоенного объема отстает от планового значения: x(t) = xe(t) = kl0t £ £ xe(t). Если X0 ‒ суммарный объем работ по проек- ту, фактическая продолжительность проекта T = = X0 ¤ (kl0) ³ T0. Причем фактические суммарные затраты на проект превысят плановое значение: C = X0 ¤ k ³ C0. Фактические суммарные затраты превышают плановое значение, фактическая эффективность ниже, а фактическая продолжительность проекта увеличилась: В рассматриваемой модели сразу после начала реализации проекта по единственному наблюдению освоенного объема или одного из относительных показателей возможно однозначно определить фактическое значение интенсивности, действительную продолжительность проекта, затрат и т.д. Обнаружив в момент времени t < T несоответствие освоенного объема (и затрат) и плановой динамики объема, возможно решение задач оперативного управления по корректировке параметров реализации проекта. Например, для завершения проекта в плановые сроки необходимо в оставшееся время (T0 – t) либо использовать ресурс в объеме В первом случае это приводит к росту суммарных фактических затрат по сравнению с плановыми на величину ∆C = X0(k0 ‒ k) ¤ k0k, а во втором случае не меняет суммарных затрат. Величина ∆C позволяет оценить перерасход средств, вызванный неправильной плановой оценкой, при условии необходимости завершения проекта в срок. Задача управления пакетом проектов состоит в следующем: распределить дополнительные стоимостные ресурсы между несколькими проектами с целью минимизации рисков несвоевременного завершения проектов. Пусть Gi (i = 1, 2, …, I) – выполняемые предприятием ОПК проекты с временем начала выполнения проектов T0 = T0(Gi)i=1, …, l и директивными сроками окончания Tдир = Tдир(Gi)i=1, …, l. Имеется дополнительный страховой ресурс C (реализуемых проектов Gi, i = 1). Считается, что в каждый проект Gi может быть вложен целочисленный вклад, не превосходящий константу Gi. Для каждого проекта Gi полагается известной монотонно возрастающая в нестрогом смысле функция fi(u), определяющая величину дохода, получаемого при вложении в данный проект вклада u. Требуется определить обеспечивающее максимальный суммарный доход распределение суммы С или ее части по проектам. Математическая модель задачи следующая: Доход fi(u) трактуется как снижение величи- ны штрафа за срыв сроков выполнения проекта при вложении дополнительного ресурса и fi(u) = = ∆ti(u)hi ‒ u, где hi ‒ величина штрафа за единицу просроченного срока завершения проекта; ∆ti(u) ‒ снижение времени выполнения проекта (критического пути), определяемое с применением метода оперативного управления. Сформулированную задачу можно трактовать как задачу поиска полной траектории, обеспечивающей максимальный суммарный доход в соответствующим образом построенной дискретной управляемой системе. Исходные данные задачи определяют систему W, управление в которой осуществляется в дискретном времени i = 0, 1, …, I – 1 (в момент i определяется вклад в сферу Gi+1). Состояния системы – пары (i, U), где i – момент дискретного времени; U – сумма, которая к данному моменту еще не распределена, здесь i ∈ {0, 1, …, I}, U ∈ {0, 1, …, С}. Начальное состояние системы – (0, C); финальными являются состояния вида (I, U). В любом нефинальном состоянии (i, U) выбор реализуемого в этом состоянии управления ut+1 осуществляется из совокупности V(i, U) = {0, 1, …, min(Сi+1, U)}; выбранная величина it+1 – размер вклада в сферу Gi+1. Под воздействием управления ut+1 система Ω из состояния (i, U) переходит в состояние (i + 1, U – ui+1), получаемый при этом доход равен fi+1(ui+1). Каждая последовательность управлений, переводящая систему из начального состояния в одно из финальных, определяет некоторое допустимое решение задачи (распределение (u1, u2, …, un) капиталовложений). Исходную задачу трактуем как задачу отыскания траектории системы W, обеспечивающей максимальный суммарный доход. Функция Беллмана для системы W определяется соотношениями: W(I, U) = 0, U ∈ {0, 1, …, С};
где i ∈{0, 1, …, I – 1}, U ∈{0, 1, …, С}. При реализации обратного метода Беллмана процесс вычислений реализуется в соответствии с записанными соотношениями. Зная, что W(I, U) = 0 при всех U, по формуле (1) находим все значения W(I – 1, U) при U ∈ {0, 1, …, S}; здесь оказывается справедливым тождество В(n – 1, U) = fn(min(Сn, U)). Далее, имея вычисленные значения W(I – 1, U), по той же формуле (1) определяем все значения W(I – 2, U), где U ∈ {0, 1, …, S}, и т.д. до тех пор, пока не будет найдена величина W(0, С) – оптимальное значение критерия в решаемой задаче. В процессе вычислений для обеспечения возможности определения оптимального распределения капиталовложений после отыскания каждого следующего значения W(i, U), где i ∈ {0, 1, …, I – 1} и U ∈ {0, 1, …, С}, для пары (i, U) отдельно фиксируем значение ui+1, на котором достигается максимум правой части (1). Прямой метод Беллмана для решения задачи заключается в последовательном вычислении значений функции В*(t, U) в порядке возрастания значений первого аргумента. При этом W*(0, U) = 0, U ∈ {0, 1, …, С};
где i ∈ {0, 1, …, I–1}, U ∈ {0, 1, …, С}. Основанные на формуле (2) вычисления заканчиваются отысканием величин W*(I, U), где U ∈ {1, 2, …, С}; максимальная из найденных величин – оптимальное значение критерия в решаемой задаче. Оптимальное решение задачи в принципе может быть получено полным перебором возможных вариантов с подсчетом значения оптимизируемого критерия для каждого из таких вариантов. Множество вариантов конечно, но число их, как правило, уже при относительно малых размерностях решаемых задач оказывается столь большим, что полный перебор практически неосуществим. Использование схемы динамического программирования дает возможность определенным образом упорядочить перебор, существенно сократив при этом число подлежащих рассмотрению вариантов. Разработанные методы управления отдельными проектами (задачи управления первого уровня) позволяют перейти к разработке метода управления пакетом проектов (задачи управления второго уровня). Управление на втором уровне осуществляется на основе оптимального распределения страхового фонда между проектами для снижения рисков их несвоевременного выполнения [7, 8]. Задача оптимального распределения затрат между проектами в общем случае является экстремальной задачей большой размерности. Опыт ре- шения подобных задач показал, что их реализация связана со значительными вычислительными трудностями, если речь идет о точном решении, или возможно лишь приближенное решение. Принимая во внимание сложность решения многоразмерных динамических задач на сетях, целесообразно применить метод динамического программирова- ния [9, 10]. Литература 1. Голенко-Гинсбург Д.И. Статистические сетевые модели планирования и управления разработками. Воронеж: Научная книга, 2010. 284 с. 2. Допира Р.В., Ягольников Д.В., Сергиенко С.В., Шароглазов В.Б., Архипов А.А. Метод сетевого планирования ввода в строй объектов информационной системы ВКО // Наукоемкие технологии в космических исследованиях Земли. 2016. Т. 8. № 1. С. 40–44. 3. Допира Р.В., Кордюков Р.Ю., Лобузько А.В., Бегле- цов А.А., Талалаев А.Б. Метод информационной поддержки вы- полнения структурно-сложных проектов // Программные продукты и системы. 2013. № 1. С. 82–87. 4. Ягольников Д.В., Кордюков Р.Ю., Сергиенко С.В., Шароглазов В.Б., Филатов А.В. Метод мониторинга процесса ввода в строй объектов информационной системы ВКО // T-Comm: Телекоммуникации и транспорт. 2016. Т. 10. № 11. С. 46–49. 5. Кофман А., Дебазей Г. Сетевые методы планирования. М.: Прогресс, 1968. 182 с. 6. Колосова Е.В., Новиков Д.А., Цветков А.В. Методика освоенного объема в оперативном управлении проектами. М.: Апостроф, 2000. 156 с. 7. Зайцев М.Г., Варюхин С.Е. Методы оптимизации управления и принятия решений. М.: Дело, 2008. 664 с. 8. Баркалов С.А., Бурков В.Н., Гилязов Н.М. Методы агрегирования в управлении проектами. М.: Изд-во ИПУ РАН, 1999. 55 с. 9. Коган Д.И. Динамическое программирование и дискретная многокритериальная оптимизация. Нижний Новгород: Изд-во НГУ им. Н.И. Лобачевского, 2004. 260 с. 10. Гаврилов Н.Н., Карамзина Н.С., Колосова Е.В., Лысаков А.В., Цветков А.В. Анализ и управление проектами. Практический курс. М.: Изд-во РЭА, 2000. 114 с. References
|
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=4374 |
Статья в формате PDF Выпуск в формате PDF (29.80Мб) |
| Статья опубликована в выпуске журнала № 4 за 2017 год. [ на стр. 721-725 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Возможности мониторинга динамики развития проекта в интеллектуальном проектном репозитарии
- Разработка прецедентного модуля для идентификации сигналов при акустико-эмиссионном мониторинге сложных технических объектов
- Технологические процессы с гибкими связями типа «звезда» для интерактивных программных систем
- Метод оценки технического уровня изделия по мониторингу рекламаций в системе управления качеством производства
- Программа моделирования температуры провода и потерь мощности на основе учета режимных и атмосферных факторов
Назад, к списку статей



 .
.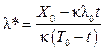 , либо увеличить интенсивность (что не всегда возможно с технологической точки зрения) до величины
, либо увеличить интенсивность (что не всегда возможно с технологической точки зрения) до величины 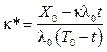 .
. при условиях:
при условиях: 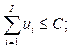 ui Î {0, 1, …, Ci}, i = 1, I.
ui Î {0, 1, …, Ci}, i = 1, I.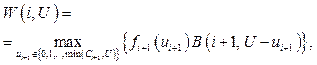 (1)
(1)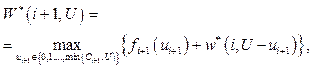 (2)
(2)