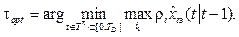Most technological processes are multifactorial, which is characterized by several parameters, and their occurrence depends on many factors. Dynamic changes in process parameters have an inconsistent nature. Moreover, random external influences are not always predictable and should be taken into account.
This article discusses the possibility of controlling the main fermentation process of beer (more precisely forecasting its optimal completion time) applying the Kalman filter.
Statement of the problem. The technological process of the main fermentation process in brewing manufacture is characterized by basic dynamic and threshold changes of parameters, such as the percentage of alcohol (A), the extract (E), temperature (To) and (pH) value [1]. The completion time of the product manufacturing process is the time when the basic parameters reach the specified (critical) values of (A ˂ Acr, E ˃Ecr, pH ˃ pHcr). The temperature of the product must be in the interval of Tocr min ≤ To ≤ Tocr max (Tocr min, Tocr max – are minimum and maximum product temperature values, at which the process is implemented).
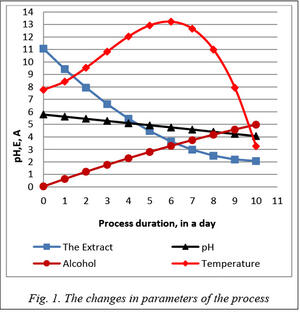 Based on the experimental data analysis [2] the equations of relationship between the values of parameters and the process time is shown in formula (1) and the graphs of this relationships are shown in figure 1.
Based on the experimental data analysis [2] the equations of relationship between the values of parameters and the process time is shown in formula (1) and the graphs of this relationships are shown in figure 1.
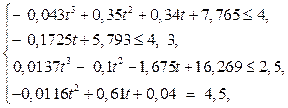 (1)
(1)
where t³0.
The process duration is defined as a maximum time to achieve specified (critical) values of all parameters. These critical values for the studied process are: То = 4; pH = 4,3; E = 2,5; A= 4,5.
It is possible to control the process duration only by changing the temperature. In the course of the process others parameters should change in accordance with the relevant rules and by the completion of the process to achieve their critical values.
The goal of an optimal process control is forecasting a minimum duration.
The basis of the optimal process control is forecasting the dynamics of the main parameters. It should be noted that the dynamics of the process parameters is affected by various random factors of natural origin (for example, the quality of product ingredients, deviation of ambient temperature from the set point, the accuracy observance of technological modes, etc.). Therefore, the process parameters’ values A(t), E(t), pH(t) at each moment of time will be of a random nature. In this context, they are presented at each current time interval (Ti, t) implementations of random functions in the process time interval Ti
The forecasting parameters process A(t), E(t), pH(t) denote by xi(t), where i is a parameter index, i = 1, 2, 3, and present it in the form of a segment of a convergent series (in the sense of mean square convergence)
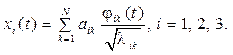 (2)
(2)
In an orthogonal basis of functions jik(t), k=1, 2, 3, ..., N, where ak – are pair wise uncorrelated random variables with zero mathematical expectations, jk(t) – functions of own integral equations of the form;
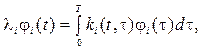 (3)
(3)
li – is its own values, independent and their correlation functions change relatively slowly in time. In this case for the evaluation of correlation functions it is possible to use the principle of moving smoothing the experimental data for each xi(t)th process parameter and write the calculated expression for them in the form
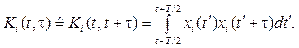 (4)
(4)
The best forecasting value of the corresponding parameter is calculated by the expression:
 , (5)
, (5)
where the sign Ù refers to a continuation, which is an extrapolation xi(t), jik(t) to the time t+Dt – point-in-time extrapolation. Obviously, because of the deterministic basis functions jik(t), k=1, 2, ..., N, are written expressions for the derivatives of the predicted process.
However, there is no general method of solving the integral equation (3).
Therefore, we will consider the process of product manufacturing with its polynomial representation in non-orthogonal basis functions followed by the estimation of the coefficients of the polynomial non-stationary adaptive Kalman filter by “external” thermal management of product manufacturing.
It is known that the mathematical structure of a non-stationary filter is similar to the mathematical structure of the stationary Kalman filter taking into account external control [3, 4]. At the input of the filter there will be a constant measuring the parameters of the process values. For practical purposes it is important not to select an orthogonal basis set of functions 1, t, t2, ..., tn [5, 6].
On the basis of 1, t, t2, …, tn extrapolation (forecasting) of the parameters for the process of product manufacturing we recorded process values and rate of changes. The results of the estimates obtained at the output of the Kalman filter are shown in the following expressions:
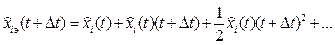
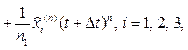
 (6)
(6)

The sign Ù denotes the estimation of appropriate values of the controlled process in the current time. At the same time the Kalman filter forms a variance-covariance matrix of extrapolation errors. Fundamentally, it is calculated by the expression:
 , (7)
, (7)
where 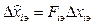 is error extrapolation tэi=t+Dt;
is error extrapolation tэi=t+Dt;
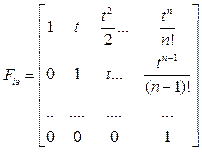
is the operator of extrapolation [7].
As a result we will obtain the necessary input data for determining the completion time of the manufac- turing process of the product. Sufficient data must contain the necessary and valid threshold region. At the input the extrapolated values of the parameters (trajectories) set the completion time for the process of product manufacturing with specific parameters.
The Kalman filter is represented by the equations shown below.
The equation of state containing external control of Markov dynamics of the parameters of the process x(t):
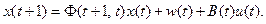 (8)
(8)
The equation of observations. It measures the parameters of x(t) dynamics:
z(t)= x(t)+ v(t). (9)
The equation for evaluating extrapolation:
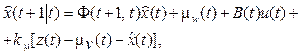 (10)
(10)
where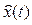 is the value of the dynamics of x(t) parameter at the next time of taking the measurement.
is the value of the dynamics of x(t) parameter at the next time of taking the measurement.
Assessment of the dynamics of x(t) parameters at the current point of time:
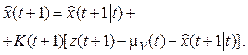 (11)
(11)
The gains in the equation for evaluating extrapolation of the parameters for x(t) dynamics:
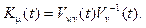 (12)
(12)
The gains in the equation for the estimation of the parameters of x(t) dynamic:
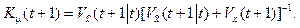 (13)
(13)
The extrapolation error:
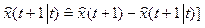 . (14)
. (14)
The covariance error of extrapolation:
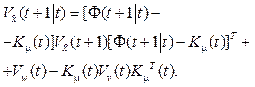 (15)
(15)
Covariance of the estimation error:
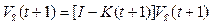 . (16)
. (16)
Here we use the following notation: t=T°, 1, 2, 3…, for the ith of the manufacturing process parameters of the product;
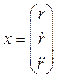 ,
, 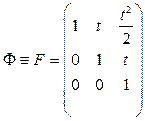 ,
,  ,
,
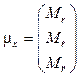 ,
,  ,
, 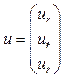 , Zºz (17)
, Zºz (17)
w is Jamming effects in the manufacturing of product process (equation of state); v is Jamming effects in the equation of observation (the measurement of the x(t) dynamics parameters).
The filter equation in the notation introduced will be used to assess the parameter of x(t) dynamics for the given state equations as algebraic equations of the second order.
The Jamming effects w(t) and v(t) can’t follow the normal Gaussian probability distribution. However, the recurrence relation of the Kalman filter remains valid and abnormal distributions w(t) and v(t) [9]:
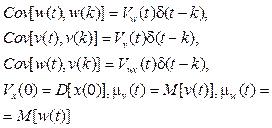 (18)
(18)
where M is the symbol of mathematical expectation
 .
.
Values are determined from physical considerations (if they are equal to 1, then there are not strengthened and not weakened).
Initial conditions:
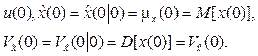
(Their values can be set based on the initial conditions of the process beginning; the result is a set of trajectories at each control point.)
The manufacturing process of the product is completed when all the observed parameters (in our case they are A, E and pH) reach the required values.
In that case under the optimal completion time of the product manufacturing process we will understand the moment in time at which the required probability of achieving all ith process parameters required values, e.g. completion parameters. This probability is calculated according to the probability density [8]
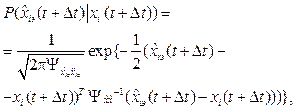 (19)
(19)
 ,
,
aiэ, biэ are the extrapolated lower and upper boundaries of the interval values of the completion indicator of the ith process parameter, calculated to a point in time tэ=t+Dt as the point of intersection of the extrapolated trajectory of the lower and upper boundary lines – the borders of the established region of the optimal values of the product completion indicator for the ith parameter. 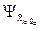 is the variance of the extrapolated values of
is the variance of the extrapolated values of  trajectory ith product component in the process of its manufacturing, which suits the value of the first element of the first row in the matrix Yiэ. Normal density is adopted due to the fact that such density has maximum entropy compared to other densities with the same first two moments as normal density. In this case the obtained result will be the best guaranteed.
trajectory ith product component in the process of its manufacturing, which suits the value of the first element of the first row in the matrix Yiэ. Normal density is adopted due to the fact that such density has maximum entropy compared to other densities with the same first two moments as normal density. In this case the obtained result will be the best guaranteed.
The estimated probability formula is written as:
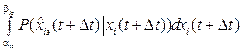 . (20)
. (20)
The application of the Gaussian probability density is based on the linearity of the non-stationary Kalman filter, forming a trajectory of completion of the ith process parameter. The completion intervals of the ith parameter for a product set by solving inequalities [9].
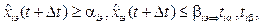 (21)
(21)
where tia and tib are the points in time of reaching trajectory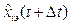 parameters of the product for the ith parameter with the speed
parameters of the product for the ith parameter with the speed 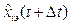 .
.
At the same time the expression 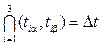 is determined by the intersection of the intervals and sets the desired optimal time, as the time of completion of the product
is determined by the intersection of the intervals and sets the desired optimal time, as the time of completion of the product 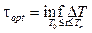 subject to achieve a desired probability of product availability.
subject to achieve a desired probability of product availability.
 However, it may be a situation in which
However, it may be a situation in which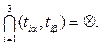 In this case, the decision about the optimal completion time of the product manufacturing process obviously should be taken only on the basis of the Pareto expression. The Pareto set is determined by the dynamics of the extrapolated trajectories of two dominant “conflicting” parameters of the manufac- tured product at an acceptable time interval [T0, TD]. To calculate the product optimal completion time we will use the formula:
In this case, the decision about the optimal completion time of the product manufacturing process obviously should be taken only on the basis of the Pareto expression. The Pareto set is determined by the dynamics of the extrapolated trajectories of two dominant “conflicting” parameters of the manufac- tured product at an acceptable time interval [T0, TD]. To calculate the product optimal completion time we will use the formula:
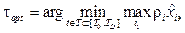 , (22)
, (22)
where ri are the weights of trajectories’ parameters of the product manufacturing process; 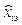 are extrapolated values of the trajectories; Tp is the Pareto set of efficient points of completion time of the product manufacturing process; i1, i2 are the dominant indexes “conflicting” parameters in the product manufacturing process.
are extrapolated values of the trajectories; Tp is the Pareto set of efficient points of completion time of the product manufacturing process; i1, i2 are the dominant indexes “conflicting” parameters in the product manufacturing process.
On the basis of the physical nature of the product process control, a control criterion should be based on the requirement of product completion for the minimum time. The control criterion must be complex, e.g. vector, and consist of two individual criteria: one of them must reflect completion and the other must reflect the time spent on product manufacturing. For the criteria formation of the product completion we will introduce the utility function
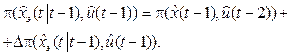 (23)
(23)
The estimated Kalman filter of the trajectory of the product manufacturing ith parameter to the current time and the extrapolated value of the trajectory at the current time depends on the decision maker. The choice of utility function depends on the decision maker with respect to the product completion. We proceed when the selected function from the terms of the decision maker disincline towards risk. In this case the utility function is nothing other than the desired criterion, which is the functional definition on the trajectory of the product manufacturing. Such a criterion is continuous, convex upwards, owing to the decision maker disinclination towards risk and, obviously, not additive. However, it is admitted by virtue of the Markov parameters of the trajectory of the product, its reduction to additive form at every current time t for each parameter. For this, we simply use the following expression:

where 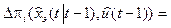 (24)
(24)
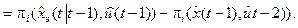
Now, taking into account the requirement to minimize the process time, it is possible to form a vector criterion process control of the product manufacturing as a maximum of the utility function of the product and the minimum time for its manufacturing can be written in the following form
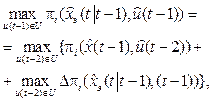 (25)
(25)
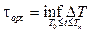 .
.
Or 
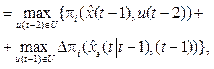 (26)
(26)
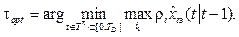
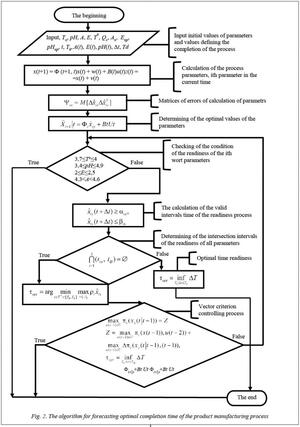
It should be noted that, the first formed criteria is written as the solution of the Bellman equation and provides feedback to the Kalman filter for optimal control. The algorithm for forecasting optimal completion time of the product manufacturing process is shown in figure 2 [10].
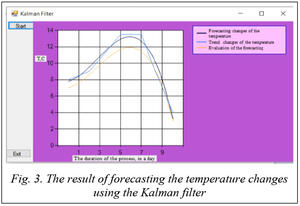 Input initial values of parameters and values defining the completion of the process (fig. 3).
Input initial values of parameters and values defining the completion of the process (fig. 3).
The algorithm is implemented in a high-level programming language C#, Microsoft Visual Studio 2015.
Conclusion. The implementation of the above algorithm, the process control based on Kalman filter in an object-oriented automated control system can optimize the product manufacturing process at various combinations of the product ingredients and the parameters, under which the process is manufactured.
References
1. Ermolaeva G.A., Kolchaeva R.A Tekhnologiya i oborudovanie proizvodstva piva i bezalkogolnykh napitkov [Technology and equipment for beer and soft drinks production]. Study guide, Moscow, IRPO, Akademiya Publ., 2000, 416 p. (in Russ.).
2. Schuurman M., Brarudi S.A. Sustainable Development Report 2010. 2011, 16 p.
3. Baranov A.M., Osipov E.V. Sintez filtra Kalmana s ispolzovaniem MatLab [Synthesis of Kalman Filter Using Matlab]. Tambov, 2010 (in Russ.).
4. Welch G., Bishop G. An Introduction to the Kalman Filter. Univ. of North Carolina at Chapel Hill, NC, 2001.
5. Ogarkov M.A. Metody statisticheskogo otsenivaniya pa- rametrov sluchaynykh protsessov [The Statistical Estimation Methods for Random Process Parameters]. Moscow, Energoatomizdat Publ., 1990, 208 p. (in Russ.).
6. Berezin I.S., Zhidkov N.P. Metody vychisleny [Calculation Methods]. Moscow, FML Publ., 1962, vol. 1, 464 p. (in Russ.).
7. Kuzmin S.Z. Osnovy teorii tsifrovoy obrabotki radiolokatsionnoy informatsii [The Basics of the Radar Data Digital Processing Theory]. Moscow, Sov. radio Publ., 1974, 432 p. (in Russ.).
8. Sage A.P., Melsa J.L. Estimation Theory with Applications to Communications and Control. McGraw-Hill Publ., US, 1971, 752 p. (Russ.ed.: B.R. Levin, Moscow, Svyaz Publ., 1976, 496 p.).
9. Albert A. Regressiya, psevdoinversiya i rekurrentnoe otsenivanie [Regression, Pseudo-Inverse and Recurrent Estimation]. Moscow, Nauka Publ., 1977, 224 p.

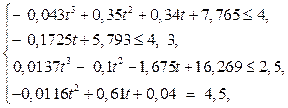 (1)
(1)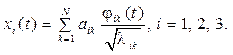 (2)
(2)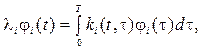 (3)
(3)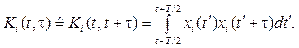 (4)
(4) , (5)
, (5)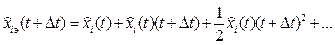
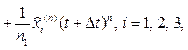
 (6)
(6)
 , (7)
, (7)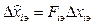 is error extrapolation tэi=t+Dt;
is error extrapolation tэi=t+Dt;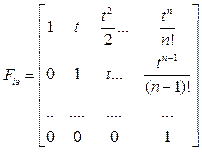
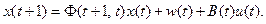 (8)
(8)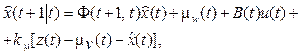 (10)
(10)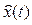 is the value of the dynamics of x(t) parameter at the next time of taking the measurement.
is the value of the dynamics of x(t) parameter at the next time of taking the measurement.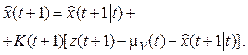 (11)
(11)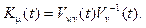 (12)
(12)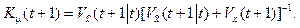 (13)
(13)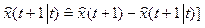 . (14)
. (14)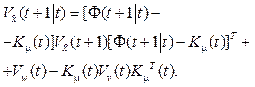 (15)
(15)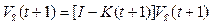 . (16)
. (16)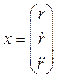 ,
, 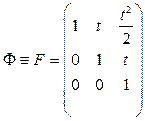 ,
,  ,
,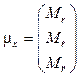 ,
,  ,
, 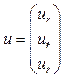 , Zºz (17)
, Zºz (17)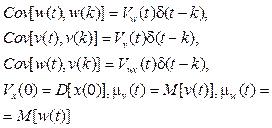 (18)
(18) .
.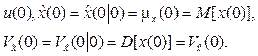
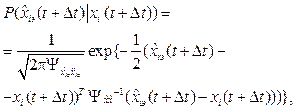 (19)
(19) ,
, 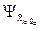 is the variance of the extrapolated values of
is the variance of the extrapolated values of  trajectory ith product component in the process of its manufacturing, which suits the value of the first element of the first row in the matrix Yiэ. Normal density is adopted due to the fact that such density has maximum entropy compared to other densities with the same first two moments as normal density. In this case the obtained result will be the best guaranteed.
trajectory ith product component in the process of its manufacturing, which suits the value of the first element of the first row in the matrix Yiэ. Normal density is adopted due to the fact that such density has maximum entropy compared to other densities with the same first two moments as normal density. In this case the obtained result will be the best guaranteed.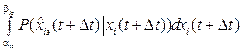 . (20)
. (20)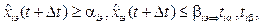 (21)
(21)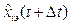 parameters of the product for the ith parameter with the speed
parameters of the product for the ith parameter with the speed 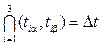 is determined by the intersection of the intervals and sets the desired optimal time, as the time of completion of the product
is determined by the intersection of the intervals and sets the desired optimal time, as the time of completion of the product 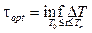 subject to achieve a desired probability of product availability.
subject to achieve a desired probability of product availability.
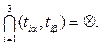 In this case, the decision about the optimal completion time of the product manufacturing process obviously should be taken only on the basis of the Pareto expression. The Pareto set is determined by the dynamics of the extrapolated trajectories of two dominant “conflicting” parameters of the manufac- tured product at an acceptable time interval [T0, TD]. To calculate the product optimal completion time we will use the formula:
In this case, the decision about the optimal completion time of the product manufacturing process obviously should be taken only on the basis of the Pareto expression. The Pareto set is determined by the dynamics of the extrapolated trajectories of two dominant “conflicting” parameters of the manufac- tured product at an acceptable time interval [T0, TD]. To calculate the product optimal completion time we will use the formula: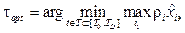 , (22)
, (22)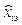 are extrapolated values of the trajectories; Tp is the Pareto set of efficient points of completion time of the product manufacturing process; i1, i2 are the dominant indexes “conflicting” parameters in the product manufacturing process.
are extrapolated values of the trajectories; Tp is the Pareto set of efficient points of completion time of the product manufacturing process; i1, i2 are the dominant indexes “conflicting” parameters in the product manufacturing process.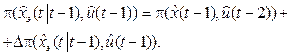 (23)
(23)
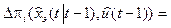 (24)
(24)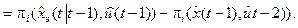
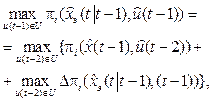 (25)
(25)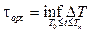 .
.
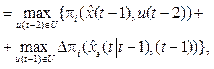 (26)
(26)