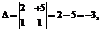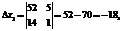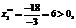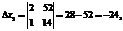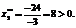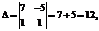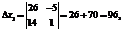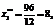Journal influence
Bookmark
Next issue
On the application of linear programming to enhance the survivability of technological processes automated control system
Abstract:The article discusses the ways to improve the safety and efficiency of a destruction complex for organophosphorus agents using development of applied mathematical methods for increasing the reliability and survivability of TPACS of a chemical weapon destruction facility when the hazard level is normal. A management problem is formalized. The problem of optimal control is formulated as a maximization problem. The problem of industrial complex operational management is formulated as a linear programming problem. The objective function of this problem is a linear function, which determines the maximum possible mass of toxic substances that is destroyed in one cycle. The coefficients of a linear function are the price of products and energy flows. Tolerance range of regime parameters of technological operations (capacity balance equation, material flows tolerances, load range) define the scope of restrictions for the objective function. The authors developed a method of determining the intervals of linear model input variables, which do not lead to a significant deviation from the found optimum and at the same time provide stability of the optimal solution when model parameters change; such intervals which indirectly contribute to the survivability of the technological system.
Аннотация:В статье рассмотрены способы повышения уровня безопасности и эффективности работы комплекса уничтоже-ния фосфорорганических отравляющих веществ при нормативном уровне опасности производства путем разработки прикладных математических методов повышения надежности и живучести АСУТП объекта уничтожения химиче-ского оружия. Проведена формализация задачи управления. Сформулирована задача оптимального управления как задача максимизации. Задача оперативного управления производственным комплексом ставится в виде задачи ли-нейного программирования. Целевая функция данной задачи – линейная функция, которая определяет максимально возможные массы отравляющих веществ, уничтожаемых за один цикл. Коэффициенты линейной функции – цена продуктов и энергетических потоков. Области допустимых значений режимных параметров технологических опера-ций (уравнения баланса емкости, допустимые отклонения материальных потоков, диапазоны нагрузок) определяют область ограничений для целевой функции. Разработана методика определения интервалов изменения входных пе-ременных линейной модели, которые не приводят к существенному отклонению от найденного оптимума и одно-временно обеспечивают устойчивость оптимального решения при изменениях параметров модели, то есть таких ин-тервалов, которые косвенно способствуют повышению живучести технологической системы.
| Authors: Matveev, Yu.N. (matveev4700@mail.ru) - Tver State Technical University (Professor), Tver, Russia, Ph.D, Grigoryev V.A. (evm@tstu.tver.ru) - Tver State Technical University, Tver, Russia, Ph.D, Stukalova N.A. (nast77@mail.ru) - Tver State Technical University, Tver, Russia | |
| Keywords: tolerance range, optimal control, technological operation, linear function, , mathematical model, a chemical weapon destruction object |
|
| Page views: 9089 |
Print version Full issue in PDF (8.21Mb) Download the cover in PDF (1.09Мб) |
Необходимость внедрения АСУ технологическими процессами (ТП) на предприятиях повышенной опасности, к которым относятся объекты уничтожения химического оружия (УХО), обусловлена тем, что причиной более 50 % возникающих аварийных и нештатных ситуаций на таких предприятиях является человеческий фактор. Поэтому любое управление такими ТП, которое может быть автоматизировано, осуществляется АСУТП. Таким образом, разработка прикладных вопросов моделирования поведения сложных систем, а именно АСУТП для экстремальных объектов, остается одной из актуальных научно-технических задач. Надежность, хотя и является важным свойством систем, представляет собой лишь одну составляющую качества АСУТП. Понятие качества можно определить как совокупность свойств системы, удовлетворяющих требованиям конечного потребителя. Оценка и обеспечение надежности АСУТП являются частью более общей задачи – оценки и обеспечения качества этих систем. Надежность необходимо исследовать во взаимосвязи с другими свойствами системы, входящими в понятие «качество», такими как живучесть, безопасность, эффективность. Свойство систем выполнять некоторые заданные функции по управлению объектом с допустимыми эксплуатационными показателями при воздействии особо существенных внешних факторов, не предусмотренных условиями нормальной эксплуатации, называют живучестью АСУТП [1]. Особенностями таких внешних факторов является то, что они обычно одновременно прикладываются к ряду элементов объекта и АСУТП. В определении живучести в отличие от определения надежности от АСУТП требуется выполнение не всех, а только некоторых функций. К тому же допускается снижение качества их выполнения до определенного предела. Обычно в свойстве живучести рассматриваются функции, обеспечивающие безопасность персонала, отсутствие неблагоприятных последствий для окружающей среды, предотвращение повреждений технологического оборудования. В данной статье авторы рассматривают возможные способы повышения уровня безопасности и эффективности работы комплекса уничтожения фосфорорганических отравляющих веществ (зарина, зомана, Vx) при нормативном уровне опасности (риске) производства путем разработки прикладных математических методов повышения надежности и живучести АСУТП объекта УХО. Структура технологического комплекса УХО (детоксикация и битумирование) является последовательной: отдельные стадии процесса соединены таким образом, что выход каждой предыдущей является входом одной последующей. Предполагается, что известно математическое описание каждой стадии процесса, которое представляется в общем виде как система уравнений: x(i)=f (i)(x(i–1), u(i)), (1) где x(i) – вектор выходных переменных i-й стадии; u(i) – вектор управления на i-й стадии, i=1, 2, …, N. На переменные выхода x(i) и управляющие воздействия u(i) накладываются ограничения, определяющие диапазон изменения переменных и связи между ними. С точки зрения математики, данные ограничения накладывают дополнительные условия, которые записываются в виде равенств и неравенств: Fj(x(i), …, x(N), u(i), …, u(N)) ³, =, £ 0, j= 1, …, k, (2) и учитываются при решении задачи оптимизации. Эффективность каждой стадии процесса может быть оценена некоторой скалярной величиной: ri = ri*(x(i), u(i)), (3) которая задается как функция, зависящая от переменных состояния стадии x(i) и управления на ней u(i). Учитывая математическое описание стадии (1), можно представить функциональную зависимость (3) как ri = ri(x(i-1), u(i)), (4) то есть как функцию состояния входа x(i-1) на i-й стадии и управления u(i), которое на ней используется. Оценку эффективности всего процесса можно определить в виде аддитивной функции результатов:
Значение показателя RN – критерия оптимальности – зависит от управляющих воздействий uN на каждой стадии процесса и является набором значений векторов u(i) на всех стадиях [2, 3]: uN= (u(1), u(2), …, u(N)). (6) Совокупность управлений uN является стратегией управления (стратегией управления многостадийным процессом). Тогда задача оптимизации процесса уничтожения (детоксикация и битумирование) формулируется как задача отыскания оптимальной стратегии:
В статье рассматриваются только установившиеся режимы работы технологических стадий. Задача статической оптимизации управления химико-технологическим комплексом (ХТК) УХО ставится в общем случае следующим образом. Определить при х2 = ƒ2(х0, х1, u1), u1ÎU1, (9) х4 = ƒ4(х2, х3, u2), u2ÎU2, (10) х9 = ƒ9(х6, х7, u3), u3ÎU3, (11) х11 = ƒ11(х9, х10, u4), u4ÎU4, (12) х11а = ƒ11а(х8, х10, u4а), u4аÎU4a, (13) х14 = ƒ14(х12, х13, u5), u5ÎU5, (14) х5 – х4 = Δ1, х6 – х5 = Δ2, х12 – х11 = Δ3, (15) хimin ≤ хi ≤ хimax, i =1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14. (16) Показатель эффективности управления (8) является самым распространенным экономическим показателем работы производства – себестоимостью. Этот показатель есть линейная функция двух переменных x и u. Коэффициенты ci и dj – удельные цены входящих веществ и энергетических потоков, которые определяют режимы работы технологических стадий. Уравнения (9)–(14) являются моделями технологических операций. Эти модели, вообще говоря, описываются известными функциями входных нагрузок и режимных параметров и, как правило, являются нелинейными функциями переменных. Области допустимых значений режимных параметров U1, U2, U3, U4, U41, U5 известны изначально и не зависят друг от друга. Уравнения баланса емкостей определяют зависимости материальных потоков различных технологических операций, которые связаны через эти емкости. Заданные значения Δ1, Δ2 и Δ3 определяют допустимые отклонения материальных потоков. Ограничения (16) задают диапазоны нагрузок, обеспечивающие нормальное прохождение технологических операций. Линеаризация задачи (8)–(16) позволила представить задачу статической оптимизации (задачу оперативного управления) комплекса УХО как задачу линейного программирования (ЛП). Задача оперативного управления технологическим комплексом УХО (8)–(16) имеет оптимальное решение: xj =x0j, j=1, …, 14. Однако возникает следующая задача: с точки зрения системного подхода проанализировать и четко установить взаимосвязи между всеми факторами (переменными) конкретной задачи ЛП [4, 5]. Для систем и процессов УХО это особенно актуально, учитывая повышенную опасность таких систем для окружающей среды и людей. Возникает необходимость в определении численных значений интервалов изменения входных переменных линейной модели, которые не приводят к существенному отклонению от найденного оптимума и одновременно обеспечивают устойчивость оптимального решения при изменениях параметров модели, то есть таких интервалов, которые косвенно способствуют повышению живучести как технологической системы, так и АСУТП. Такие исследования получили название – анализ модели задачи ЛП при известном оптимальном решении [6, 7]. В статье предложен метод получения квазиоптимального инвариантного решения задачи ЛП. Идея предлагаемого метода заключается в следующем. Определяются оптимальные решения прямой и двойственной симметричных задач ЛП для ситуации, описываемой линейной моделью. Пусть прямая задача ЛП имеет вид
где A= Тогда двойственная задача ЛП будет иметь вид
где Теория двойственности для задач ЛП утверждает, что для оптимальных решений прямой и двойственной задач должно выполняться условие дополняющей нежесткости:
где Из условия (23) следует: если какая-либо двойственная переменная в оптимальном решении zk0¹0, то остаток ресурса bk0=0. Это означает, что этот ресурс исчерпан, и данное обстоятельство не позволяет больше увеличивать численное значение целевой функции W (16). С практической точки зрения, большой интерес представляет исследование поведения оптимального решения Для большей иллюстративности и понимания продолжим рассуждения на числовом примере. Пусть какая-то операция описывается задачей ЛП W=x1+x2®max при ограничениях –3x1+4x2£24, 3x1+5x2³15, 2x1+5x2£53, (24) 7x1–5x2£28, x1,2³0. Приводим (24) к стандартному виду: W=0–(–x1–x2)®max, y1= 24–(–3x1+4x2), y2= –15–(–3x1–5x2), y3= 53–(2x1+5x2), (25) y4= 28–(7x1–5x2), x1,2³0, y1,2,3,4³0. Решаем задачу симплекс-методом. Исходная симплекс-таблица
Произведя две итерации, получим оптимальное решение задачи (24): Конечная симплекс-таблица
Таким образом: На рисунке представлена геометрическая интерпретация решения задачи (24). Из оптимального решения прямой задачи (конечная симплекс-таблица) можно определить оптимальное решение двойственной задачи [8]:
Теневая цена ресурса b3: Это свидетельствует о том, что ресурс b3 дефицитнее, весомее ресурса b4 в четыре раза и любое отклонение в сторону его уменьшения (по разным случайным и неслучайным причинам) приведет к тому, что полученное оптимальное решение прямой задачи (24) станет не только неоптимальным, но вообще недопустимым, то есть точка Е на рисунке окажется за пределами области допустимых решений (ОДР). В отличие от подходов, реализованных в работах [6, 7, 10] и направленных на недопущение уменьшения Другими словами, предлагается уменьшить на определенную величину ОДР, получить квазиоптимальное, но устойчивое (интервальное) решение, не прибегая к решению стохастической задачи ЛП, которая не всегда оказывается корректной и приводит к получению приемлемого для практики решения. В задаче (24) уменьшим запас ресурса b3 на одну единицу, то есть положим в модели b3=52, запас ресурса b4 уменьшим на две единицы, то есть положим b4=26. Это означает, что линии ОДР (см. рис.) DE и AE параллельным переносом сдвинутся внутрь ОДР. Определим точку пересечения линии y3*=0 и y4*=0, решив для этого систему уравнений:
То есть по сравнению с оптимальным решением x0=(9, 7) точка пересечения прямых y3*=y40=0 сдвинулась внутрь ОДР. x*=(82/3; 614/15) Уменьшим также W до значения W=14. Это значит, что линия целевой функции будет пересекать ребра ОДР y3*=0 и y4*=0 Определим координаты этих точек пересечения, решив две системы линейных уравнений:
Для системы (27): Точка K пересечения целевой функции W и ограничения y3*=0 имеет координаты x1**=6, x2**=8, то есть K(6; 8). Для системы (28): То есть точка Н пересечения W и ограничения y4*=0 имеет координаты Н(8; 6). Итак, определяются интервалы изменения переменных x1Î[6; 8] и x2Î[6; 8], где численное значение целевой функция задачи (24) инвариантно изменению переменных x1 и x2 (отрезок КН). С практической точки зрения, это обстоятельство позволяет утверждать, что при изменении переменной x1 в интервале [6; 8] и переменной x2 в интервале [6; 8] значение целевой функции W=14 не изменяется. Не важно, какие возмущения на x1 и x2 будут наложены и какой закон распределения они имеют, в указанных интервалах обеспечивается квазиоптимальное инвариантное значение целевой функции задачи ЛП, а значит, и устойчивость процесса управления технологической системой и живучесть АСУТП. Разработанный метод получения квазиоптимального решения задач ЛП был включен в состав алгоритмического обеспечения АСУТП объекта УХО «Щучье», передан в опытную эксплуатацию и позволил повысить живучесть системы, что подтверждается отсутствием аварийных ситуаций на объекте. Литература 1. Ковалев А.П., Якимшина В.В. О живучести объектов энергетики // Промышленная энергетика. 2006. № 1. С. 20–26. 2. Бутенко Д.В. Автоматизированная система прогно- зирования на основе цикла смены качественных состоя- ний системы // Программные продукты и системы. 2011. № 3. С. 35–41. 3. Смирнов К.Е. Многомерный анализ данных в системах недоопределенных вычислений // Программные продукты и системы. 2010. № 4. С. 71–74. 4. Стукалова Н.А., Матвеев Ю.Н., Долженко А.Б. Автоматизированная система управления технологическими процессами уничтожения химического оружия // Науковедение. 2014, № 4 (23); URL: http//naukovedenie.ru/PDF/54TVN414.pdf (дата обращения: 24.05.2015). 5. Мелихова О.А., Мелихова З.А. Имитационное моделирование сложных технологических процессов // Изв. ЮФУ. 2004. № 3. С. 27–34. 6. Цыпкин Я.З. Адаптация и обучение в автоматических системах. М.: Наука, 1968. 460 с. 7. Вальд А. Последовательный анализ; [пер. с англ.]. М.: Физматлит, 1960. 328 с. 8. Таха Х. Введение в исследование операций: в 2-х кн.; [пер. с англ.]. М.: Мир, 1985. 356 с. 9. Мишта П.В., Бызов П.Г. Применение систем моделирования при разработке АСУТП // Изв. ВолгГТУ. 2010. № 4. С. 65–71. 10. Антонова Г.М., Цвиркун А.Д. Оптимизационно-имитационное моделирование для решения проблем оптимизации современных сложных производственных систем // Проблемы управления. 2005. № 5. С. 44–50. |
| Permanent link: http://swsys.ru/index.php?page=article&id=4024&lang=&lang=en&like=1 |
Print version Full issue in PDF (8.21Mb) Download the cover in PDF (1.09Мб) |
| The article was published in issue no. № 3, 2015 [ pp. 28-32 ] |
Perhaps, you might be interested in the following articles of similar topics:
- Математическая модель защиты компьютерной сети от вирусов
- Концепция математического и компьютерного моделирования тепловых процессов в электронных системах
- Модели планирования производства изделий, основанных на нанотехнологиях
- Архитектура интеллектуальной системы оптимального управления эволюцией многостадийных процессов в нечеткой динамической среде
- Комплекс программных средств для исследования погрешности измерений экспериментального лазерного кругломера
Back to the list of articles
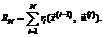 (5)
(5)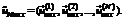 (7)
(7)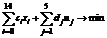 (8)
(8)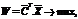 (17)
(17)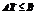 , (18)
, (18)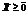 , (19)
, (19)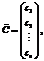
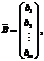
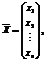
 .
.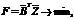 (20)
(20)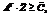 (21)
(21)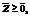 (22)
(22)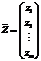 – вектор-столбец двойственных переменных zi, i = 1, …, m.
– вектор-столбец двойственных переменных zi, i = 1, …, m. (23)
(23)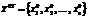 – оптимальное решение прямой задачи;
– оптимальное решение прямой задачи; 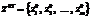 – оптимальное решение двойственной задачи.
– оптимальное решение двойственной задачи.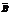 . Некоторые подобные исследования приведены в [7–9].
. Некоторые подобные исследования приведены в [7–9].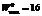 при
при 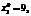
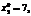
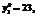
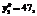
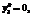
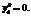
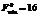 при
при 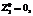
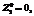
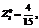
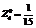 .
.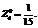
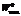 в задачах ЛП, в настоящей статье предлагается ради достижения приемлемого уровня безопасности и живучести системы УХО допустить незначительное уменьшение выигрыша операции
в задачах ЛП, в настоящей статье предлагается ради достижения приемлемого уровня безопасности и живучести системы УХО допустить незначительное уменьшение выигрыша операции 
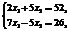 (26)
(26)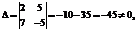

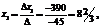
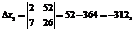
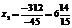 .
.
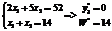 (27)
(27)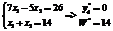 (28)
(28)