Identification theory solves problems of constructing mathematical models of dynamic systems according to the observations of their behaviour. The object identification step is one of the most important steps while constructing mathematical models of objects or processes. The quality of the model relies on this step. Therefore, the quality of control that is based on this model or results of a research with this model also rely on this step.
Dynamic object identification is one of the basic problems which can be solved using many different methods. For example statistic analysis or neural networks [1] can be used. Object identification is complicated if noises are present in the source data, some of the object parameters change according to unknown laws or the exact number of the object parameters is unknown. In such cases neural network can be applied for dynamic object identification. There are a lot of different types of neural networks that can be used for dynamic object identification.
Among different neural network architectures applicable for dynamic object identification a class of neural networks based on self-organizing maps (SOM) can be noted. Neural networks of such type will be given special attention in this article due to their wider spread and successful application in solving different kinds of problems of recognition [2], identification [3], etc. A number of biomorphic neural networks, architecture of which is the result of studying the structure of the cerebral cortex of mammals, will also be considered.
SOM-based neural networks can be used for dynamic object identification
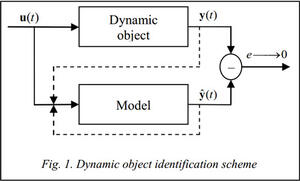
Problem definition. Identification of a dynamic object that receives a vector of input parameters u(t) and has a corresponding output vector y(t) can be described as finding the type of a model of this object, that has an output  and finding parameters of this model such that minimize error
and finding parameters of this model such that minimize error  of this model (see fig. 1).
of this model (see fig. 1).
 Suppose that there is a vector of input parameters u(t),
Suppose that there is a vector of input parameters u(t),  and a sequence of output vectors y(t),
and a sequence of output vectors y(t),  , where T is a number of input-output pairs. We will consider the solution of the object identification problem as a definition of the function type f that will define the model of identified object:
, where T is a number of input-output pairs. We will consider the solution of the object identification problem as a definition of the function type f that will define the model of identified object:
 ,
,
where  is a vector of output parameters of the model. At a single moment of time the input of the model takes current known measured values of the input parameters along with nu<
is a vector of output parameters of the model. At a single moment of time the input of the model takes current known measured values of the input parameters along with nu<
Also we will consider solution of this problem in the following form:
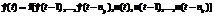 ,
,
where 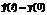 ,
, 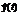 is a vector of output parameters of the model. This identification scheme has recurrent connections and at a single moment of time the input of the model takes current known measured values of the input parameters of the object along with nu<
is a vector of output parameters of the model. This identification scheme has recurrent connections and at a single moment of time the input of the model takes current known measured values of the input parameters of the object along with nu<
 Vector quantized temporal associative memory (VQTAM). VQTAM is a modification of self-organizing maps which can be used for identification of dynamic objects [4, 5]. The structure of this network is similar to regular SOM structure. The key difference is in the way that weight vectors are organized. The input vector x(t) of this network is split into two parts: xin(t), xout(t). The first part of the input vector xin(t) contains information about the inputs of the dynamic object and its outputs at previous time steps. The second part of the input vector xout(t) contains information about the expected output of the dynamic object corresponding to the input xin(t). The weights vector is also split into two parts in a similar way [5]. Thus
Vector quantized temporal associative memory (VQTAM). VQTAM is a modification of self-organizing maps which can be used for identification of dynamic objects [4, 5]. The structure of this network is similar to regular SOM structure. The key difference is in the way that weight vectors are organized. The input vector x(t) of this network is split into two parts: xin(t), xout(t). The first part of the input vector xin(t) contains information about the inputs of the dynamic object and its outputs at previous time steps. The second part of the input vector xout(t) contains information about the expected output of the dynamic object corresponding to the input xin(t). The weights vector is also split into two parts in a similar way [5]. Thus  and
and 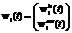 , where xi(t) is weights vector of the i-th neuron,
, where xi(t) is weights vector of the i-th neuron,  is the part of the weights vector that contains information on the inputs corresponding to xin(t), and
is the part of the weights vector that contains information on the inputs corresponding to xin(t), and 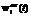 is the part of the weights vector that contains information on the outputs corresponding to xout(t). The first part of the input vector contains information on the process inputs and its previous outputs:
is the part of the weights vector that contains information on the outputs corresponding to xout(t). The first part of the input vector contains information on the process inputs and its previous outputs:
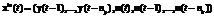 ,
,
where ny<
Each vector in the learning sample consists of a pair of vectors (y(t), u (t)) and the sample should contain not less than max(nu, ny) vectors. Vectors y(t) are the measured output parameters of the process at time step t and u(t) are the input parameters of the process at the same time step.
 After presenting a subsequent input vector x(t), combined of several vectors from the learning sample, to the network the winner neuron is determined only by the xin(t) part of the vector:
After presenting a subsequent input vector x(t), combined of several vectors from the learning sample, to the network the winner neuron is determined only by the xin(t) part of the vector:
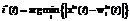 ,
,
where i*(t) is a number of the winner neuron at time step t.
For weight modification a modified SOM weight modification rule is used:
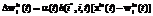 ,
,
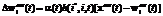 ,
,
where 0
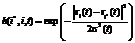 ,
,
where ri(t) and ri*(t) are positions on the map of the i-th and i*-th neurons, s(t)>0 determines the radius of the neighbourhood function at time step t. When the winner neuron i* is defined, the output of the network is set to  (learning scheme of the network is presented on fig. 2).
(learning scheme of the network is presented on fig. 2).
On the test sample VQTAM's input takes only xin(t) part of the input, which is used to define the winner neuron, and the output of the network is set to  (the working scheme is presented on fig. 3). Vector
(the working scheme is presented on fig. 3). Vector  can be interpreted as the predicted output
can be interpreted as the predicted output 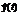 of the dynamic object at time step t. It is worth mentioning that this network can be successfully used to identify objects with both continuous and non-continuous outputs.
of the dynamic object at time step t. It is worth mentioning that this network can be successfully used to identify objects with both continuous and non-continuous outputs.
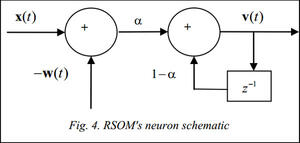
Recurrent self-organizing map (RSOM). In RSOM unlike conventional SOMs with recurrent connections, a decaying in time vector of outputs is introduced for each neuron. This vector is used to determine the winner neuron and in maps weights modification [6, 7].
The network inputs vector x(t) is represented as follows:
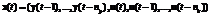 ,
,
where ny<
Output of each neuron is determined according to the following equation: 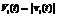 , where vi(t)=(1–a)vi(t–1)+a(x(t)–wi(t)), a is the output decay factor (0, k is the neuron count.
, where vi(t)=(1–a)vi(t–1)+a(x(t)–wi(t)), a is the output decay factor (0, k is the neuron count.
After presenting a subsequent input vector to the network a winner neuron is determined as the neuron with minimal output [7]: 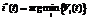 .
.
To modify the weights a modified conventional SOM rule is used: 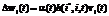 , where 0
, where 0
When the learning process is complete, the network is presented again with the learning sample and clusterizes it. Each cluster can be approximated with an individual model, for example a linear function fi(t) for the i-th cluster. Thus, after presenting the learning sample a linear function is defined for each vector of this sample. These functions can be used to determine the output value at the next time step.
This process can be speeded up using algorithms for constructing local linear models while training the neural network. Such method is applicable in case if the size of the output is scalar, thus y(t) and 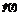 are scalar. This method is applicable only to the objects with outputs that can be described with continuous functions. Each neuron of the RSOM network is associated with a matrix Ai(t) that contains coefficients of the corresponding linear model:
are scalar. This method is applicable only to the objects with outputs that can be described with continuous functions. Each neuron of the RSOM network is associated with a matrix Ai(t) that contains coefficients of the corresponding linear model:
 .
.
The output value of the network is defined according to the following equation:
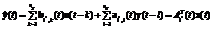 ,
,
where Ai*(t) is a matrix of coefficients associated with the winner neuron i*(t). Matrix Ai*(t) is used for linear approximation of model output.
While constructing the local linear models simultaneously with the training of the neural network an additional rule to modify the coefficients of the linear model is needed: 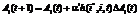 , where 0
, where 0
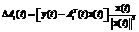 ,
,
where y(t) is desired output of the model for the x(t) input.
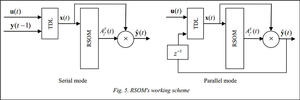
Thus, at each step of the network training a modification of the model coefficients is performed along with modification of the weights of neurons. On the test sample after an input vector is presented to the network a winner neuron i*(t) is chosen. Than a corresponding coefficients matrix Ai*(t) of the linear model is calculated. Using the determined matrix the output of the model is defined by the equation:  . The working scheme is shown on igure 5.
. The working scheme is shown on igure 5.
Modular self-organizing maps. Modular self-organizing maps are presented in Tetsuo Furukawa's works [8, 9]. Modular SOM has a structure of an array which consists of functional modules that are actually trainable neural networks, such as multilayer perceptrons (MLP), but not a vector, as in conventional self-organizing maps. In case of MLP-modules modular self-organizing map finds features or correlations in input and output values simultaneously building a map of their similarity. Thus, a modular self-organizing map with MLP modules is a self-organizing map in a function space but not in a vector space [9].
These neural network structures can be considered biomorphic, as their emergence is due to research of the brain structure of mammals [10], and confirmed by a number of further studies [11]. The basis of the idea of the cerebral cortex structure is a model of cellular structure, where each cell is a collection of neurons, a neural column. Columns of neurons are combined in more complex structures. In this regard it was suggested to model the individual neural columns with neural networks [11]. This idea has formed the basis of the modular neural networks.
In fact, the modular self-organizing map is a common SOM, where neurons are replaced by more complex and autonomous entities such as other neural networks. Such replacement requires a slight modification of the learning algorithm.
In the algorithm proposed by Furukawa [9] at the initial stage the network receives the i-th sample of the input data corresponding to I functions which will be mapped by the network, and the error is calculated for each network module: 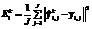 , where k is a module number for which the error is calculated, J is number of vectors in the sample,
, where k is a module number for which the error is calculated, J is number of vectors in the sample,  is an output of the k-th module, yi,j is expected output of the network on suggested set of input data. Winner module is calculated as the module that minimizes the error
is an output of the k-th module, yi,j is expected output of the network on suggested set of input data. Winner module is calculated as the module that minimizes the error 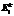 :
: 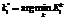 .
.
As soon as the winner module is defined, the adaptation process takes place and the weights of the module are being modified according to one of learning algorithms suitable for the networks of this type. After that the weights of the main SOM are being modified. In this process parameters (weights) of each module are considered as the weights of the SOM and are modified according to standard learning algorithms suitable for conventional SOMs.
In this study SOMxVQTAM and SOMxRSOM networks were developed. They are SOMs with modules of VQTAM type and SOMs with modules of RSOM type respectively. Further some application results of such networks will be reviewed.
Modular network where VQTAM networks are used as modules (SOMxVQTAM) that was developed during this work is trained by combination of the learning algorithm of modular SOMs and VQTAM learning algorithm. When a subsequent learning sample vector is presented to the network, outputs of all VQTAM networks (that are used as modules) are calculated. Then a winner-module is selected as the module with the output with less deviation from the expected output for the presented sample vector. Weights of the winner-module network are modified according to the VQTAM learning algorithm. The set of weight vectors of the whole module-network is treated as one of the weight vectors of the whole modular network, and the weight modification is done according to the standard f SOM learning algorithms.
In case of a modular network, where RSOM networks are used as modules (SOMxRSOM) also developed during this work, learning is held according to similar algorithm.
Using SOM-based neural networks for dynamic object identification
For some experiments and comparisons of the algorithms the neural networks of types VQTAM, RSOM, SOMxVQTAM and SOMxRSOM were tested on samples that were used in 2008 to identify the winners at neural networks forecasting competition [12]. Results of this competition were used for this study as there is a detailed description of the place definition method used for all competitors. Also a fair amount of different algorithms took part in this competition and there was a description for the most of those algorithms as well as the learning and testing samples which allowed a comparative analysis of the neural networks described in this paper with other advanced algorithms. To determine the place in the table of the competition organizers [12] it is suggested to forecast 56 steps for each of the 111 samples. For each of the resulting predictions a symmetric mean absolute percentage error SMAPE was calculated:
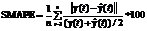 ,
,
where y(t) is a real state of the object at time step t,  is an output of the model at time step t, n is a number of vectors in the testing sample (56 for this competition). Then the place in the table was determined from the average error for all of 111 samples.
is an output of the model at time step t, n is a number of vectors in the testing sample (56 for this competition). Then the place in the table was determined from the average error for all of 111 samples.
Each of the 111 samples had different lengths; those samples represented a monthly measure of several macroeconomic indicators.
Results table for different forecasting algorithms
|
№
|
Algorithm name
|
SMAPE, %
|
|
1
|
Wildi
|
19,9
|
|
2
|
Andrawis
|
20,4
|
|
3
|
Vogel
|
20,5
|
|
4
|
D'yakonov
|
20,6
|
|
5
|
Noncheva
|
21,1
|
|
6
|
Rauch
|
21,7
|
|
7
|
Luna
|
21,8
|
|
8
|
Lagoo
|
21,9
|
|
9
|
Wichard
|
22,1
|
|
10
|
Gao
|
22,3
|
|
– –
|
SOMxVQTAM
|
23,4
|
|
11
|
Puma-Villanueva
|
23,7
|
|
– –
|
VQTAM
|
23,9
|
|
12
|
Autobox (Reilly)
|
24,1
|
|
13
|
Lewicke
|
24,5
|
|
14
|
Brentnall
|
24,8
|
|
15
|
Dang
|
25,3
|
|
16
|
Pasero
|
25,3
|
|
17
|
Adeodato
|
25,3
|
|
– –
|
RSOM
|
25,7
|
|
18
|
undisclosed
|
26,8
|
|
19
|
undisclosed
|
27,3
|
|
– –
|
SOMxRSOM
|
27,9
|
This and other tests that were concluded lead to a suggestion that modular modification gives a significant increase if accuracy in case of VQTAM modules, but modular networks are more sensitive to changes of learning parameters. The higher SMAPE in case of the SOMxRSOM modular network compared to RSOM network can be explained by the fact that RSOM itself contains local models and during the learning process of the SOMxRSOM network those local models are treated as weight vectors for the whole SOMxRSOM network. But the local models are constructed for different parts of the input data and the local model corresponding to one of the neurons of one of the RSOMs are most likely to be constructed for the different part of the input data compared to the local model contained in another RSOM for the neuron on the same position.
Conclusion
In this article several SOM-based neural networks that can be successfully used for dynamic object identification have been described. New modular networks with VQTAM and RSOM networks as modules where developed. In case of the VQTAM modules a significant increase in quality of identification is achieved in comparison to regular VQTAM networks. In case of neural networks where RSOMs are used as modules quality of the identification is decreased that can be explained by the features of algorithm for constructing linear models. This results show that it is possible to increase the quality of the identification by simply joining neural networks in to modular structures.
References
1. Haykin S. Neural Networks – a comprehensive foundation. 2nd ed. Prentice Hall Int., Inc., 1998, 842 p.
2. Efremova N., Asakura N., Inui T. Natural object recognition with the view-invariant neural network. Proc. of 5th int. conf. of Cognitive Science (CoSci). 2012, June 18–24, Kaliningrad, Russia, pp. 802–804.
3. Trofimov A., Povidalo I., Chernetsov S. Usage the self-learning neural networks for the blood glucose level of patients with diabetes mellitus type 1 identification. Science and education. 2010, no. 5, available at: http://technomag.edu.ru/doc/142908.html (accessed July 10, 2014) (in Russ.).
4. Souza L.G.M., Barreto G.A. Multiple local ARX modeling for system identification using the self-organizing map. Proc. of European Symp. on Artificial Neural Networks – Computational Intelligence and Machine Learning. Bruges, 2010.
5. Koskela T. Neural network methods in analyzing and modelling time varying processes. Espoo, 2003, pp. 1–72.
6. Varsta M., Heikkonen J. A recurrent Self-Organizing Map for temporal sequence processing. Springer Publ., 1997, pp. 421–426.
7. Lotfi A., Garibaldi J. Applications and Science in Soft Computing. Advances in Soft Computing Series, vol. 24, Springer Publ., 2003, pp. 3–8.
8. Tokunaga K., Furukawa T. SOM of SOMs. Neural Networks. 2009, vol. 22, pp. 463–478.
9. Tokunaga K., Furukawa T. Modular network SOM. Neural Networks. 2009, vol. 22, pp. 82–90.
10. Logothetis N.K., Pauls J., Poggiot T. Shape representation in the inferior temporal cortex of monkeys. Current Biology. 1995, vol. 5, pp. 552–563.
11. Vetter T., Hurlbert A., Poggio T. View-based Models of 3D Object Recognition: Invariance to imaging transformations. Cerebral Cortex. 1995, vol. 3, pp. 261–269.
12. Artificial Neural Network & Computational Intelligence Forecasting Competition. 2008. Available at: http://www.neural-forecasting-competition.com/NN5/results.htm (accessed July 10, 2014).
Литература
1. Haykin S. Neural Networks – a comprehensive foundation. 2nd ed. Prentice Hall Int., Inc., 1998, 842 p.
2. Efremova N., Asakura N., Inui T. Natural object recognition with the view-invariant neural network. V Междунар. конф. по когнитивной науке: тез. докл. (18–24 июня 2012 г.), Калининград). 2012. С. 802–804.
3. Трофимов A.Г., Повидало И.С., Чернецов С.А. Использование самообучающихся нейронных сетей для идентификации уровня глюкозы в крови больных сахарным диабетом 1-го типа // Наука и образование. 2010. №. 5; URL: http://technomag.edu.ru/doc/142908.html (дата обращения: 10.07.2014).
4. Souza L.G.M., Barreto G.A. Multiple local ARX modeling for system identification using the self-organizing map. Proc. of European Symp. on Artificial Neural Networks – Computational Intelligence and Machine Learning. Bruges, 2010.
5. Koskela T. Neural network methods in analyzing and modelling time varying processes. Espoo, 2003, pp. 1–72.
6. Varsta M., Heikkonen J. A recurrent Self-Organizing Map for temporal sequence processing. Springer Publ., 1997, pp. 421–426.
7. Lotfi A., Garibaldi J. Applications and Science in Soft Computing. Advances in Soft Computing Series, vol. 24, Springer Publ., 2003, pp. 3–8.
8. Tokunaga K., Furukawa T. SOM of SOMs. Neural Networks. 2009, vol. 22, pp. 463–478.
9. Tokunaga K., Furukawa T. Modular network SOM. Neural Networks. 2009, vol. 22, pp. 82–90.
10. Logothetis N.K., Pauls J., Poggiot T. Shape representation in the inferior temporal cortex of monkeys. Current Biology. 1995, vol. 5, pp. 552–563.
11. Vetter T., Hurlbert A., Poggio T. View-based Models of 3D Object Recognition: Invariance to imaging transformations. Cerebral Cortex. 1995, vol. 3, pp. 261–269.
12. Artificial Neural Network & Computational Intelligence Forecasting Competition. 2008. Available at: http://www.neural-forecasting-competition.com/NN5/results.htm (accessed July 10, 2014).
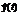 and finding parameters of this model such that minimize error
and finding parameters of this model such that minimize error  of this model (see fig. 1).
of this model (see fig. 1).
 and a sequence of output vectors y(t),
and a sequence of output vectors y(t), 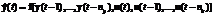 ,
,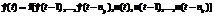 ,
,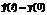 ,
, 
 and
and 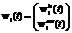 , where xi(t) is weights vector of the i-th neuron,
, where xi(t) is weights vector of the i-th neuron,  is the part of the weights vector that contains information on the inputs corresponding to xin(t), and
is the part of the weights vector that contains information on the inputs corresponding to xin(t), and 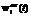 is the part of the weights vector that contains information on the outputs corresponding to xout(t). The first part of the input vector contains information on the process inputs and its previous outputs:
is the part of the weights vector that contains information on the outputs corresponding to xout(t). The first part of the input vector contains information on the process inputs and its previous outputs: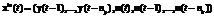 ,
,
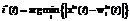 ,
,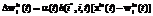 ,
,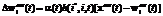 ,
,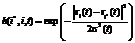 ,
, (learning scheme of the network is presented on fig. 2).
(learning scheme of the network is presented on fig. 2).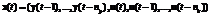 ,
,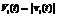 , where vi(t)=(1–a)vi(t–1)+a(x(t)–wi(t)), a is the output decay factor (0, k is the neuron count.
, where vi(t)=(1–a)vi(t–1)+a(x(t)–wi(t)), a is the output decay factor (0, k is the neuron count.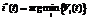 .
.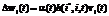 , where 0
, where 0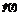 are scalar. This method is applicable only to the objects with outputs that can be described with continuous functions. Each neuron of the RSOM network is associated with a matrix Ai(t) that contains coefficients of the corresponding linear model:
are scalar. This method is applicable only to the objects with outputs that can be described with continuous functions. Each neuron of the RSOM network is associated with a matrix Ai(t) that contains coefficients of the corresponding linear model: .
.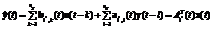 ,
,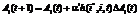 , where 0
, where 0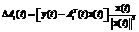 ,
,
 . The working scheme is shown on igure 5.
. The working scheme is shown on igure 5.
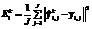 , where k is a module number for which the error is calculated, J is number of vectors in the sample,
, where k is a module number for which the error is calculated, J is number of vectors in the sample,  is an output of the k-th module, yi,j is expected output of the network on suggested set of input data. Winner module is calculated as the module that minimizes the error
is an output of the k-th module, yi,j is expected output of the network on suggested set of input data. Winner module is calculated as the module that minimizes the error 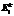 :
: 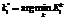 .
.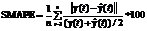 ,
,