Journal influence
Bookmark
Next issue
On some unsolved problems of the Mathematica system
The article was published in issue no. № 2, 2013 [ pp. 148-154 ]Abstract:The capabilities of the program complex Mathematica at its application for analytic and numerical computa-tions are described. The number of examples shows that the issues of processing (simplification) of rational fractional expres-sions involving the general form powers have been implemented in the Maple system more carefully than in the Mathematica system. The article demonstrates an error in the Mathematica system that leads to an incorrect work of the user’s program at a function body change. For each example of symbolic or symbolic-numeric computations the alternate routes for solving the emerged problem are proposed as far as possible. One more problem of the Mathematica system has been revealed by the ex-amples of the computations of two-dimensional gas dynamics problems: the program written in the language of this system calculates by one thousand times slower than the Fortran code.
Аннотация:Описываются возможности программного комплекса Mathematica при его применении для аналитических вычислений и численных расчетов. На ряде примеров показано, что в системе Maple более тщательно, чем в системе Mathematica, проработаны вопросы обработки (упрощения) дробно-рациональных выражений, содержащих степени общего вида. Продемонстрирована ошибка в системе Mathematica, которая приводит к неправильной работе программы пользователя при смене тела функции. По каждому примеру символьных или символьно-численных вычислений предлагаются по возможности обходные пути решения возникшей проблемы. На примерах расчетов двухмерных задач газовой динамики выявлена еще одна проблема системы Mathematica: программа, написанная на языке этой системы, считает в тысячу раз медленнее, чем Фортран-программа.
| Authors: (Evgenii.Vorozhtsov@gmail.com) - , Russia, Ph.D | |
| Keywords: fortran, expressions simplification, analytic and numerical computations, mathematica system |
|
| Page views: 8343 |
Print version Full issue in PDF (7.68Mb) Download the cover in PDF (1.35Мб) |
Современное состояние теоретической математики и развитие информационных технологий привели к созданию мощных прикладных программных средств, весьма полезных для прило- жений в области науки и инженерии, а также процесса подготовки специалистов. Одним из таких программных продуктов является система Mathematica [1]. Она была задумана как система, автоматизирующая труд научных работников и математиков. Версии системы Mathematica, начиная со второй, являются мировыми лидерами среди компьютерных систем символьной математики для персональных компьютеров (ПК), обеспечивающими не только возможности выполнения численных расчетов с выводом их результатов в самом изысканном графическом виде, но и проведение особо трудоемких аналитических вычислений и преобразований. В настоящее время система Mathematica оптимизирована под новейшие операционные системы и аппаратное обеспечение, поэтому пригодна любая система, нужная пользователю (см. подробнее www.wolfram.com/mathematica/features/system-requirements.html). Mathematica 8 имеется в наличии на платформах Microsoft Windows, Apple Mac, Linux. Обширный список книг, посвященных либо описанию элементов системы, либо ее разнообразным применениям, представлен на сайте http://library.wolfram.com/infocenter/Books/. Система Mathematica является одним из самых мощных средств поддержки научных исследований, прикладного проектирования и обучения специалистов, аспирантов и студентов. Программный комплекс Mathematica содержит широкий спектр математических методов, вычислительных алгоритмов и компьютерных программ для теоретических и прикладных исследований. Комплекс снабжен мощной графической системой визуализации полученных решений. Как уже было отмечено, система Mathematica позволяет выполнять на компьютере трудоемкие аналитические вычисления. При ее практическом применении для аналитических вычислений крайне важно, чтобы результат вычислений был правильным. Если пользователь системы по ряду критериев замечает, что полученный системой Mathematica результат неверен, то в зависимости от сложности разработанной Mathematica-программы ее создатель может потратить на поиск ошибки от одного до нескольких дней. После того как ошибка будет локализована, создателю программы понадобится еще некоторое время на то, чтобы заменить ту часть программы, где какие-то встроенные операторы или функции системы Mathematica работают неправильно, на операторы, обеспечивающие правильный результат. В подавляющем большинстве случаев удается найти обходные пути решения возникшей локальной проблемы благодаря большому количеству функций, имеющихся в системе Mathematica. Ясно, что любые внутренние ошибки или недоработки системы снижают эффективность работы пользователя. Есть и еще более важный аспект, связанный с наличием внутренних ошибок системы Mathematica: в некоторых случаях результат, выдаваемый системой, внешне может выглядеть правдоподобно, но на самом деле является ошибочным, что в итоге может привести к авариям тех технологических изделий, при создании которых в железе использовались результаты аналитических вычислений, выполненных в Mathematica. Поэтому в тех случаях, когда нет каких-либо контрольных математических соотношений, которым должны удовлетворять полученные на компьютере аналитические результаты, необходимо дублирование аналитических вычислений в другой системе, например в Maple, REDUCE. Приведем примеры аналитических, символьно-численных и численных расчетов, в которых использовались лицензионные копии программных пакетов Mathematica 4.1.0 (лицензия L2989-2426) и Maple 7 (лицензия P/N: 01-0701-00-B-SN-A-E-0, serial number 693366959). Кроме того, использовалась лицензионная копия операционной системы Windows XP Professional (лицензия E85-05798). Ранее в работе [2] на 542 коротких задачах были проанализированы возможности символьных вычислений с помощью семи систем аналитических вычислений общего назначения: Axiom, Derive, Macsyma, Maple, Mathematica, MuPAD, REDUCE. В 13 из 542 примеров система Mathematica выдала полностью неправильные ответы. В настоящей статье приводятся некоторые примеры, когда система Mathematica выдает либо неправильный результат, либо правильный, но имеющий громоздкий вид, который невозможно упростить с помощью встроенных функций системы. По каждому такому примеру предлагаются по возможности обходные пути решения возникшей проблемы. Следует отметить, что ни один из приведенных примеров не входит в число тех 542, которые были рассмотрены в [2]. Недостаточная эффективность функций упрощения выражений Рассмотрим задачу из вузовского курса математического анализа о вычислении суммы S=2+2∙3x+3∙4x2+…+n(n–1)xn–2. Решим ее с помощью системы Mathematica, воспользовавшись встроенной функцией Sum[…]: S=Sum[j* * (j–1)*x^(j–2),{j, 2, n}]. Получаем ответ в виде
Ясно, что это выражение можно упростить, поделив числитель и знаменатель на x. Чтобы не делать это вручную, воспользуемся имеющейся в системе Mathematica встроенной функцией Simplify[…], предназначенной для упрощения выражений: S=Simplify[S]. Однако вместо ожидаемого упрощения функция Simplify[…] выдала прежний результат (1). Другая встроенная функция, PowerExpand[…], позволяет упрощать выражения, содержащие степенные функции, но и ее применение к (1) оставило выражение (1) без изменения. Вот какой результат дает применение функции Expand[S], которая раскладывает сложную дробь S на составляющие элементарные дроби:
Из (2) видно, что в каждой элементарной дроби система Mathematica произвела сокращение и числителя, и знаменателя на множитель x. Поэтому теперь можно надеяться, что повторное применение функции Simplify[…] уже к сумме дробей (2) даст желаемый, более простой по сравнению с (1) результат. Но при упрощении выражения (2) система Mathematica зачем-то умножила и числитель, и знаменатель итогового выражения на x, вследствие чего вновь получилось исходное выражение (1). В системе Mathematica имеется еще функция Together[S], которая приводит сумму дробей к общему знаменателю. Поскольку в знаменателях в (2) нет множителя x, можно надеяться, что эта функция выдаст результат в желаемом упрощенном виде. Тем не менее результат применения этой функции к (2) снова привел к выражению (1). Посмотрим, какой результат дает использование программного комплекса Maple для решения той же задачи: > S:=simplify(sum(j*(j–1)*x^(j–2), j=2, ..., n));
Таким образом, функция simplify(…), имеющаяся в Maple, выдала результат в искомой, более простой форме, чем (1). Задача о безвихревом обтекании неподвижной сферы потоком идеальной несжимаемой жидкости является сравнительно простым примером трехмерной задачи гидродинамики. Предполагается, что на бесконечности поток жидкости направлен вдоль оси
где r=(x2+y2+z2)1/2. Получим теперь выражение (3) с помощью системы Mathematica, осуществив обезразмеривание с помощью этой системы: r=Sqrt[x^2+y^2+z^2]; fi=V0*r*(1+1/2*(R/r)^3)*z/r; u=D[fi, x] u1=u/.{x®R*x1, y®R*y1, z®R*z1} u1a=PowerExpand[u1/V0]; Print[\"u1a=\", u1a]. Здесь используются следующие обозначения: fi – потенциал скорости; V0=U∞, x1, y1, z1 – безразмерные пространственные координаты; u1a – безразмерная составляющая скорости вдоль оси x. В результате работы вышеприведенной программы получается следующее выражение для u1a:
Из (4) видно, что функция PowerExpand[u1/V0] не заметила наличие общего множителя R2∙5/2=R5 в знаменателе: u1b=Simplify[u1/V0]; Print[\"u1b=\", u1b];
Функция Simplify[u1/V0] смогла обнаружить общий множитель R2 только в основании степени. И наконец, u1c=PowerExpand[u1b]; Print[\"u1c=\",u1c];
Из (5) видно, что комбинация функций Simplify[…] и PowerExpand[…] привела к правильному результату. Посмотрим, за сколько шагов можно получить результат (5) с помощью системы Maple: >u:=–3*R^3*V0*x*z/(2*(x^2+y^2+z^2)^(5/2)); u1c: = simplify(subs(x=x1*R, y=y1*R, z=z1*R, u/V0), assume=positive); В результате работы этой Maple-программы получается формула (5), то есть в Maple-функции simplify(…) имеется анализ выражений, содержащих степени. Некоторые особенности выполнения операций с комплексными величинами в системе Mathematica Кроме возможности выполнения основных арифметических операций над комплексными числами, в системе Mathematica имеются еще встроенные функции Re[z], Im[z], Conjugate[z], Abs[z], Arg[z]. Назначение каждой из этих функций ясно из их названий. Для обозначения мнимой единицы i= z=5–4I; Print[“Re(z)=“, Re[z],”; Im(z)=“, Im[z]]; Ответ: Re(z)=5, Im(z)=–4. Пусть теперь z=cos2x+ +i tg(x)/x, где x – вещественная переменная. Применение функции Re[z] в этом случае дает ответ Re(z)=Re(cos2(x))–Im(tg(x)/x), потому что в системе Mathematica предполагается, что каждая из функций cos2(x) и tg(x)/x может быть комплексной. Функция ComplexExpand[z] осуществляет упрощение комплексного числа z=a+ib в предположении, что оба выражения a и b вещественны. Пример: z=Cos[x]^2+I*Tan[x]/x; ComplexExpand[Re[z]]. Ответ получается в виде Re(z)=cos2x. Однако операция zim1=ComplexExpand[Im[z]] приводит к ответу
вместо ожидавшегося
Используя известные тригонометрические соотношения, нетрудно преобразовать формулу (6) к виду (7). Однако правая часть равенства (6) требует для своей записи 20 символов, а правая часть (7) – 7 символов, если принять горизонтальную черту, отделяющую числитель от знаменателя, за один символ. В системе Mathematica имеется встроенная функция ByteCount[expr], которая подсчитывает количество байтов, используемых внутренне системой для хранения выражения expr. Например, обращение ByteCount[zim1] дает для правой части (6) ответ 320 байт. Теперь попытаемся упростить выражение (6) с помощью функции Simplify[…]: zim2=Simplify[zim1] дает ответ (7). Далее ByteCount[zim2] дает ответ 104 байта. То есть внутреннее представление выражения (6) в системе Mathematica в три раза длиннее, чем в случае выражения (7). Опасность появления громоздких выражений типа (6) в процессе символьных вычислений на компьютере состоит в том, что если (6) используется на следующих этапах аналитической процедуры, то это может привести к многократному разбуханию итоговых выражений. Кроме того, резко ухудшаются для пользователя обозримость и понимание итоговых результатов. Поэтому желательно выполнять многоэтапные аналитические процедуры в интерактивном режиме. Как только на одном из этапов появляется подозрительно громоздкое выражение типа (6), нужно попытаться упростить его с помощью одной из следующих функций: Simplify[…], FullSimplify[…], PowerExpand[…], ExpandAll[…]. Иногда помогает комбинация Simplify[Expand[…]]. Посмотрим, как система Maple решает задачу нахождения мнимой части комплексного числа z=cos2x+i tg(x)/x. Функция evalc(…) является в системе Maple аналогом функции ComplexExpand[…] системы Mathematica. Итак, в системе Maple имеем: z:=cos(x)^2+tan(x)/x*I; evalc(Im(z)). Ответ получается в виде (7). Таким образом, функция evalc(…) сразу выдает ответ, оптимальный с точки зрения его длины. Вернемся к системе Mathematica. В поисках простого альтернативного пути получения Im(z) в оптимальном виде (7) можно воспользоваться таким определением мнимой части числа z: Im(z) – это коэффициент при i. Для нахождения коэффициентов при некоторой переменной в системе имеется функция Coefficient[…]. Воспользуемся ею: z=Cos[x]^2+I*Tan[x]/x; zim=Coefficient[z, I]. (8) В этом случае система Mathematica выдает следующее диагностическое сообщение: Coefficient:: ivar : I is not a valid variable. More…, не выдавая никакого результата. Эту ситуацию можно обойти в системе Mathematica, заменив I в строке (8) на другую букву, скажем, j: Coefficient[z/.I®j, j]. Ответ получается в оптимальном виде (7). На основании изложенного можно сделать вывод о том, что в системе Maple более тщательно, чем в системе Mathematica, реализовано упрощение аналитических выражений. Пример неправильной работы Mathematica-программы при смене тела функции Предположим, что в пользовательской Mathematica-программе имеется параметр M, который необходимо задавать в начале программы и можно и нужно варьировать с целью получения наилучшего результата, допустим, с точки зрения требования минимума погрешности. Для сохранения информации об уже сосчитанных вариантах важно сохранять в программе информацию об уже рассмотренных значениях параметра M. Это также удобно и потому, что легко будет вернуться к одному из уже сосчитанных вариантов, который оказался наилучшим среди всех других. Сохранить информацию об уже использованных значениях M можно очень просто: M=5; M=10; M=15; M=20. При этом самый последний оператор присваивания отменяет любой из предыдущих операторов присваивания вида M=…, так что можно быть уверенным, что Mathematica-программа пользователя выполнит очередной расчет со значением M=20. На практике так всегда и происходит. Рассмотрим следующую Mathematica-програм- му: f[x_]:=x*x/; x>1; expr1=y^2–f[x]*z/.x®2. Здесь первая строка определяет функцию в случае, когда x>1. Система выдает правильный результат вычисления во второй строке: expr1=y2–4z. Теперь предположим, что на некотором этапе аналитических вычислений необходимо заменить тело функции f[x_] на другое, например такое: f[x_]:=–x/; x≠1. Очевидно, новое определение функции должно отменить предыдущее. Пусть теперь в следующей строке программы нужно вычислить выражение expr2=expr1^2–f[x]*z/.x®2. Система Mathematica выдает такой ответ: expr2=(y2–4z)2–4z. Этот ответ, очевидно, является неправильным, поскольку f[2]=–2 в соответствии с новым определением функции f[x_]. То есть система проигнорировала новое определение функции f[x_]:=–x/; x≠1 и продолжает использовать старое f[x_]:=x*x/; x>1. Приведем решение данной проблемы в рамках системы Mathematica: f1[x_]:=–x/; x≠1; expr2a=expr1^2–f[x]*z/.f[x]®f1[x] expr2=expr2a/.x®2. Очевидно, что система Mathematica выдала правильный ответ: expr2 = (y2 – 4z)2 + 2z. Медленная скорость численных расчетов в системе Mathematica Многие инженерные задачи описываются математически системами уравнений в частных производных: это, например, задачи аэрогидродинамики, магнитной гидродинамики, теории упругости и т.д. Наибольшую вычислительную трудоемкость имеют задачи, решения которых зависят от двух или трех пространственных переменных и времени t. Применение современных суперкомпьютеров и распараллеливания вычислений позволяет уже сегодня успешно решать многие прикладные многомерные задачи. Оперативность анализа результатов, получаемых при компьютерном моделировании многомерных задач, заметно возрастает при использовании средств компьютерной графики. Поэтому, например, широко известный пакет программ ANSYS Fluent (www.ansys.com) интегрирует в себе не только собственно программы для численного расчета задач газовой динамики, строительной механики и электромагнетизма, но и некоторое количество процедур компьютерной графики для визуализации результатов многомерных расчетов. Поскольку вычислительная система Mathematica уже изначально интегрировала в себе средства и для символьных вычислений, и для численных расчетов, и для графической визуализации результатов с помощью многочисленных встроенных функций компьютерной графики, то она представляется привлекательной для специалистов, занимающихся численным моделированием разнообразных прикладных задач. В [3] приведены примеры численного решения тех сравнительно простых одно-, двух- и трехмерных задач механики сплошных сред, которые могут быть сосчитаны с приемлемым расходом машинного времени в рамках системы Mathematica при достаточно умеренном общем количестве узлов пространственной расчетной сетки. В [4] была успешно осуществлена попытка применения системы Mathematica для численного решения двухмерных задач газовой динамики на криволинейных пространственных расчетных сетках. Однако оказалось, что разработанная Mathematica-программа считала во много раз медленнее, чем соответствующая Фортран-программа. Это известно разработчикам рассматриваемой системы. С целью ускорения численных расчетов в системе Mathematica они рекомендуют использовать встроенную функцию Compile[…]. Однако ее применение во многих местах Mathematica-программы, описанной в [4], уменьшило машинное время, требуемое для решения двухмерных задач газовой динамики, только в 5/3=1,67 раза, но не в 20 раз, как это декларировалось в [1]. Уравнения Эйлера, являющиеся одной из основных математических моделей для задач газовой динамики, имеют следующий вид для двухмерного течения невязкого нетеплопроводного сжимаемого газа:
где x, y – декартовы постранственные координаты; t – время и
Здесь p, ρ, u, v обозначают давление, плотность, составляющие скорости; E=ε+(1/2)(u2+v2), ε – удельная внутренняя энергия; H=E+(p/ρ). Используется уравнение состояния идеального газа p=(γ–1)ρε, γ=const>1. В [5] был подробно описан явный TVD-метод применительно к уравнениям (9), (10), поэтому здесь не приводятся расчетные формулы этого метода, который в зависимости от числового значения присутствующего в нем параметра j в подобластях гладкого течения имеет либо второй, либо третий порядок точности по пространственным переменным. Применяются ограничители потоков, а также осреднение по Роу. В этом методе, как и в других TVD-методах, производится переключение с высокого порядка аппроксимации на первый в областях ударных волн и контактных разрывов с целью получения монотонных профилей численного решения. Задача об отражении косой ударной волны от стенки часто используется для тестирования новых численных методов решения уравнений (9), (10). Точное решение этой тестовой задачи представляет собой кусочно-постоянную функцию и находится численно с машинной точностью с помощью теории косых ударных волн [3]. В предлагаемых ниже примерах расчетов вводилось значение φ=π/6 для угла между фронтом падающей ударной волны и осью x (см. рис. 1). Численное решение находилось методом установления. В начальный момент времени все поле течения задавалось равным значениям невозмущенного сверхзвукового втекающего потока, заданным выше для подобласти 1, то есть начальное течение газа параллельно оси x. Критерий сходимости разностного решения wn к предельному стационарному решению брался в виде Res(n)<ε, где ε – задаваемое пользователем малое положительное число;
где
С небольшой погрешностью можно полагать, что двухмерные задачи газовой динамики считаются в системе Mathematica в тысячу раз медленнее, чем на Фортране. Такое неблагоприятное соотношение расходов машинного времени делает систему Mathematica неприемлемой для численного решения сложных многомерных задач аэрогидродинамики. Следует отметить, что система Mathematica написана на языке Си, разработанном позже языка Фортран. Поэтому компиляторы с языка Си вобрали в себя более поздние разработки в области теории программирования. В связи с этим логично ожидать, что Си-компиляторы должны производить не менее эффективные по скорости вычислений рабочие программы (exe-файлы), чем Фортран-компиляторы. На этом фоне крайне медленная скорость вычислений в арифметике машинных чисел с плавающей запятой в системе Mathematica выглядит довольно странно. Система Mathematica имеет большое количество встроенных функций компьютерной графики, которые позволяют получать высококачественные графики кривых, изображения поверхностей, изолиний и т.п. Чтобы использовать эти возможности в целях оперативной визуализации результатов численного решения сложных многомерных задач аэрогидродинамики и математической физики, автор реализовал достаточно простой интерфейс между Фортран-программой и системой Mathematica. Реализация этого интерфейса свелась к следующему: по окончании основного счета в Фортран-программе в этой же программе был организован вывод результатов счета во внешний файл или в несколько внешних файлов в формате системы Mathematica. А на языке системы Mathematica написана небольшая программа, обеспечивающая графическую визуализацию результатов счета в форме, нужной исследователю. Выход из Фортран-компилятора и вход в Mathematica-программу требуют 3–4 сек. времени пользователя, затем Mathematica-программа запускается на счет нажатием клавиш Shift Enter. Она считывает массивы числовых результатов из внешних файлов, созданных Фортран-программой, и через несколько секунд пользователь уже видит на экране монитора результаты расчета в графическом виде. <img data-cke-saved-src="uploaded/image/2013-2/image563.gif" src="uploaded/image/2013-2/image563.gif" alt="\" Подпись:"="" width="299" height="342" align="left">На рисунке 2 приведены результаты численного расчета по Фортран-программе задачи об отражении косой ударной волны от твердой стенки, полученные счетом на установление по методу [5] на равномерной сетке из 160´40 ячеек; параметр метода j=1/3, что обеспечивает третий порядок точности метода по пространственным переменным в подобластях гладкого течения. Все эти графические результаты были получены с помощью авторской небольшой Mathematica-программы, которая считывала массивы числовых результатов из внешних файлов, созданных Фортран-программой. На рисунке 2а показаны линии постоянных чисел Маха M= На основании изложенного можно сделать следующие выводы. Как показывают приведенные примеры, в системе Maple более тщательно, чем в системе Mathematica, проработаны вопросы обработки (упрощения) дробно-рациональных выражений, содержащих степени общего вида. Продемонстрирована ошибка в системе Mathematica, которая приводит к неправильной работе программы пользователя при смене тела функции. На примере численного решения известной модельной двухмерной задачи газовой динамики показано, что эти задачи считаются в системе Mathematica в тысячу раз медленнее, чем на Фортране. Такое неблагоприятное соотношение расходов машинного времени делает систему Mathematica неприемлемой для численного решения сложных многомерных задач аэрогидродинамики. Автор выражает благодарность д.ф.-м.н. В.П. Шапееву за предоставление примера неправильной работы Mathematica-программы при смене тела функции. Литература 1. Wolfram S., The Mathematica Book, 3rd Ed. Cambridge, UK: Cambridge Univ. Press, 1996, 1403 p. 2. Wester M., A critique of the mathematical abilities of CA systems, Computer Algebra Systems: A Practical Guide, Chichester, UK: John Wiley & Sons, 1999, pp. 25–60. 3. Kiselev S.P., Vorozhtsov E.V., Fomin V.M., Foundations of Fluid Mechanics with Applications: Problem Solving Using Mathematica. Boston: Birkhäuser, 1999, 575 p. 4. Ganzha V.G., Vorozhtsov E.V., Implementation of aerodynamic computations with Mathematica, Proc. 2nd Workshop on Computer Algebra in Scientific Computing, Munich, May 31–June 4, 1999, Berlin, Heidelberg: Springer-Verlag, 1999, pp. 101–114. 5. Chakravarthy S.R., Osher S., A new class of high accuracy TVD schemes for hyperbolic conservation laws, AIAA Paper, 1985, no. 85-0363, 11 p. |
| Permanent link: http://swsys.ru/index.php?page=article&id=3482&lang=en |
Print version Full issue in PDF (7.68Mb) Download the cover in PDF (1.35Мб) |
| The article was published in issue no. № 2, 2013 [ pp. 148-154 ] |
Back to the list of articles
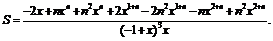 (1)
(1)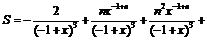
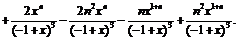 (2)
(2)
 декартовой системы координат
декартовой системы координат  . Решение рассматриваемой задачи зависит от трех размерных координат
. Решение рассматриваемой задачи зависит от трех размерных координат 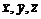 . Пусть
. Пусть  – размерные составляющие вектора скорости жидкости вдоль осей соответственно
– размерные составляющие вектора скорости жидкости вдоль осей соответственно  – размерное давление жидкости. Обезразмеривание независимых и зависимых переменных в рассматриваемой задаче делается по формулам:
– размерное давление жидкости. Обезразмеривание независимых и зависимых переменных в рассматриваемой задаче делается по формулам: 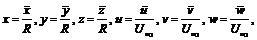
 где R – размерный радиус сферы; U∞ – скорость невозмущенного потока; ρ – плотность жидкости. Для определенности предполагается, что центр сферы находится в начале координат (0, 0, 0) системы координат Oxyz. Тогда точное решение рассматриваемой задачи получается с помощью теории потенциала скорости, так что, например, составляющая скорости u имеет вид
где R – размерный радиус сферы; U∞ – скорость невозмущенного потока; ρ – плотность жидкости. Для определенности предполагается, что центр сферы находится в начале координат (0, 0, 0) системы координат Oxyz. Тогда точное решение рассматриваемой задачи получается с помощью теории потенциала скорости, так что, например, составляющая скорости u имеет вид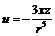 , (3)
, (3)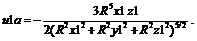 (4)
(4)
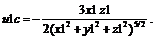 (5)
(5)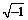 в системе зарезервирована буква I. Пример:
в системе зарезервирована буква I. Пример: (6)
(6)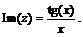 (7)
(7) (9)
(9)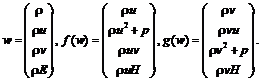 (10)
(10) (11)
(11)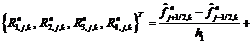
 n – номер временного слоя (n=0, 1, 2, …);
n – номер временного слоя (n=0, 1, 2, …);  – разностные аппроксимации потоков f(w) и g(w) в (1) по методу [5]; верхний индекс T обозначает операцию транспонирования; h1, h2 – шаги равномерной прямоугольной расчетной сетки в плоскости (x, y).
– разностные аппроксимации потоков f(w) и g(w) в (1) по методу [5]; верхний индекс T обозначает операцию транспонирования; h1, h2 – шаги равномерной прямоугольной расчетной сетки в плоскости (x, y).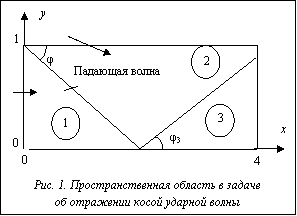 Для численного решения данной задачи были созданы две программы: одна на языке системы Mathematica, другая на языке Фортран-90. Результаты расчетов по обеим программам совпали. Все расчеты были выполнены на ПК с процессором фирмы Intel, тактовая частота 3 ГГц. Для выполнения 2 600 временных шагов по Mathematica-программе потребовалось 22 457 сек., или более 6 часов машинного времени. Фортран-программа выполнила этот же расчет за 21,45 сек. Таким образом, система Mathematica считает эту двухмерную задачу в 1 047 раз медленнее, чем Фортран-программа. Были также проведены расчеты этой же задачи по обеим программам на более грубой сетке из 80´20 ячеек, сосчитано 1 600 шагов по t. В этом случае Mathematica-программа выполнила расчет за 3 455 сек., а Фортран-программа – за 3,36 сек. Соответствующее отношение 3 455/3,36= =1 028,28. Расхождение в величинах замедления счета 1 047 и 1 028 объясняется тем хорошо известным фактом, что, чем больше промежуточных выдач делается при счете в системе Mathematica, тем медленнее она считает. В обоих вариантах счета – на сетках 160´40 и 80´20 – информация о невязке решения выдавалась через каждые 50 шагов по t. На сетке 160´40 было сделано 2 600 шагов, на сетке 80´20 – гораздо меньшее число шагов по t.
Для численного решения данной задачи были созданы две программы: одна на языке системы Mathematica, другая на языке Фортран-90. Результаты расчетов по обеим программам совпали. Все расчеты были выполнены на ПК с процессором фирмы Intel, тактовая частота 3 ГГц. Для выполнения 2 600 временных шагов по Mathematica-программе потребовалось 22 457 сек., или более 6 часов машинного времени. Фортран-программа выполнила этот же расчет за 21,45 сек. Таким образом, система Mathematica считает эту двухмерную задачу в 1 047 раз медленнее, чем Фортран-программа. Были также проведены расчеты этой же задачи по обеим программам на более грубой сетке из 80´20 ячеек, сосчитано 1 600 шагов по t. В этом случае Mathematica-программа выполнила расчет за 3 455 сек., а Фортран-программа – за 3,36 сек. Соответствующее отношение 3 455/3,36= =1 028,28. Расхождение в величинах замедления счета 1 047 и 1 028 объясняется тем хорошо известным фактом, что, чем больше промежуточных выдач делается при счете в системе Mathematica, тем медленнее она считает. В обоих вариантах счета – на сетках 160´40 и 80´20 – информация о невязке решения выдавалась через каждые 50 шагов по t. На сетке 160´40 было сделано 2 600 шагов, на сетке 80´20 – гораздо меньшее число шагов по t.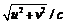 , где
, где 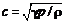 – скорость звука. На рисунке 2б сплошная линия – точное решение, штриховая – результат расчета по методу [5]. На рисунке 2в показана невязка (3) в случае метода [5]. Видно, что требуется 2 400 шагов во времени для обеспечения падения нормы невязки решения до уровня машинных ошибок округления 10–10–10–12.
– скорость звука. На рисунке 2б сплошная линия – точное решение, штриховая – результат расчета по методу [5]. На рисунке 2в показана невязка (3) в случае метода [5]. Видно, что требуется 2 400 шагов во времени для обеспечения падения нормы невязки решения до уровня машинных ошибок округления 10–10–10–12.