Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Алгоритм комплексной оптимизации режимов электроэнергетической системы с использованием обобщенных критериев подобия
Аннотация:Предлагается алгоритм комплексной оптимизации режимов электроэнергетической системы с использованием метода критериального программирования. Разработанная методика основана на методах теории подобия, критери-ального анализа и геометрического программирования, она позволяет оптимизировать целевую функцию, представ-ленную в виде миксиномов, степенью сложности больше единицы, с учетом ограничений, представленных в виде равенств и неравенств. Указанные достоинства дают возможность производить комплексную оптимизацию системы по всем параметрам режима: напряжению, активной и реактивной мощности, потерям электроэнергии – одновременно с учетом всех электротехнических законов. Предложенная методика критериального программирования использовалась для оптимизации перетоков реактивной мощности в сетях 110 кВ ОАО «МРСК Центра» – «Смоленскэнерго» с целью уменьшения потерь активной мощности, а также для комплексной оптимизации режимов неоднородной сложнозамкнутой электрической сети 110/330 кВ.
Abstract:In this article we propose an algorithm of power system optimization using criteria-based programming. This method is based on the theory of similarity, criteria-based analysis and geometric programming. It makes possible to optimize the efficiency function (consists of arbitrary polynomials with the degree of complexity more than one) with the limitations in the form of equations and inequalities. These advantages allow to optimize the power system modes by different characteristics (voltage, active and reactive power, power loss) with the account of all electrical laws. This method of the criteria-based programming was used for optimization of reactive power flows in the 110 kV power system of «IDGC of Center» – «Smolenskenergo» to reduce active power losses and for optimization of complex heterogeneous 110/330 kV power system.
| Авторы: Кавченков В.П. (vpkavchenkov@mail.ru) - Смоленский филиал Национального исследовательского университета МЭИ (профессор), Смоленск, Россия, доктор технических наук, Солопов Р.В. ( sfmei_ees@mail.ru) - Смоленский филиал Национального исследовательского университета МЭИ (ст. преподаватель ), Смоленск, Россия | |
| Ключевые слова: технико-экономические задачи., потери электроэнергии, электроэнергетические системы, критериальное программирование, оптимизация |
|
| Keywords: technical and economic problems, power losses, power systems, criteria-based programming, optimisation |
|
| Количество просмотров: 8726 |
Версия для печати Выпуск в формате PDF (5.29Мб) Скачать обложку в формате PDF (1.21Мб) |
В современных рыночных условиях для обеспечения надежности и эффективности функционирования электроэнергетической системы России необходимо оптимальное управление режимами ее работы. Особенность электроэнергетической отрасли – большое количество оптимизируемых параметров, которые значительно усложняют решение задачи технико-экономической оптимизации на стадиях проектирования, реконструкции и эксплуатации: выбор структуры, параметров и схем электрических соединений электростанций, расчет установившихся режимов, переходных процессов и устойчивости электроэнергетических систем, разработка методов контроля и анализа качества электроэнергии и мер по его обеспечению. Для решения таких задач предлагается использовать методику критериального программирования, разработанную на кафедре электроэнергетических систем филиала МЭИ в г. Смоленске [1]. В критериальном программировании критерии подобия [2] играют роль особых переменных, с помощью которых исходная задача оптимизации решается в два основных этапа: – сначала формулируется и решается задача определения численного значения критериев подобия; – затем формулируется и решается задача нахождения оптимальных значений параметров и соответствующего им значения целевой функции. Математическая формулировка решения оптимизационной задачи методом критериального программирования включает следующие этапы. 1. Формулируется исходная оптимизационная задача, в которой целевая функция
ограничения типа равенств
и типа неравенств
записываются в виде миксиномов. 2. Формируется функция Лагранжа, включающая целевую функцию и ограничения типа равенств:
и на ее основе записывается матрица размерностей
число строк в которой равно числу слагаемых функции Лагранжа, а число столбцов на единицу больше числа оптимизируемых параметров. 3. Из матрицы a выделяется неособенная матрица a1, ранг которой равен n+1. При необходимости используются перестановка строк матрицы и соответствующая перегруппировка слагаемых функции Лагранжа. Если ранг матрицы a меньше n+1, следует уточнить формулировку исходной оптимизационной задачи: возможно, уменьшить число оптимизируемых параметров. 4. Вычисляется вспомогательная матрица
число столбцов которой на единицу больше числа оптимизируемых параметров (N=n+1), а число строк на единицу меньше разности числа слагаемых функции Лагранжа и числа оптимизируемых параметров (K=M–(N+1)). 5. Формируется и решается система уравнений для вычисления критериев подобия. Эта система включает линейную часть, которая получается на основе транспонированной матрицы размерностей с учетом s-функции
представленную в виде матричного уравнения
выражающего зависимость основных критериев подобия p1 от дополнительных критериев подобия p2, и системы линейных уравнений, полученных в результате логарифмирования переменных
и выражающих зависимость дополнительных критериев от основных. 6. Сформированная система уравнений решается относительно искомых критериев подобия. 7. Формируется и решается система уравнений для вычисления оптимальных значений параметров и соответствующего значения целевой функции:
8. Проверяется выполнение ограничений типа неравенств, которые могут учитываться методом множителей Лагранжа, методом активного набора, методом штрафных функций. 9. Если есть необходимость, рассматривается задача анализа технико-экономической устойчивости целевой функции к отклонению параметров от оптимального значения. Это осуществляется по исходному уравнению, записанному в критериальном виде Достоинства предлагаемого критериального метода решения оптимизационных задач в следующем: – использование технико-экономических критериев подобия для решения оптимизационных задач позволяет проводить комплексное исследование в критериальной форме и распространить полученные результаты путем масштабных преобразований на все подобные объекты; – применение метода критериального программирования для решения неканонических оптимизационных задач со степенью сложности более единицы, с использованием основных и дополнительных критериев подобия расширяет круг решаемых задач, в том числе для неканонических задач с миксиномами, с учетом ограничений типа равенств и неравенств, накладываемых на целевую функцию; – использование технико-экономических критериев как обобщенных констант значительно сокращает объем вычислений при решении сложных многопараметрических оптимизационных задач. Данная методика критериального программирования использовалась для оптимизации перетоков реактивной мощности в сетях 110 кВ «МРСК Центра» – «Смоленскэнерго» с целью уменьшения потерь активной мощности и для комплексной оптимизации режимов неоднородной сложнозамкнутой электрической сети 110/330 кВ [3, 4]. Литература 1. Кавченков В.П., Карасев Д.Д., Солопов Р.В. Сравнение методов критериального анализа и геометрического программирования при решении оптимизационных задач электроэнергетики // Электротехника, электромеханика и электротехнологии. Энергетика. Экономика и менеджмент: тр. науч.-технич. конф. Смоленск. СФМЭИ (ТУ). 2001. Т. 1. 2. Веников В.А. Теория подобия и моделирования (применительно к задачам электроэнергетики). М.: Высш. шк., 1984. 439 с. 3. Холмский В.Г. Расчет и оптимизация режимов электрической сети. М.: Высш. шк., 1975. 280 с. 4. Карасев Д.Д., Солопов Р.В. Минимизация потерь мощности в электрических сетях с высокой степенью неоднородности // Электричество. 2002. № 10. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=3392&lang= |
Версия для печати Выпуск в формате PDF (5.29Мб) Скачать обложку в формате PDF (1.21Мб) |
| Статья опубликована в выпуске журнала № 1 за 2013 год. [ на стр. 101-103 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Теоретический подход к управлению социально-техническими системами
- Репрезентативность метрик на основе событий процессора Intel Sandy Bridge при анализе времени обработки данных в памяти
- Программный комплекс для расчета процесса нанесения покрытия в псевдоожиженном слое
- Комплекс программного обеспечения для оптимизации надежности однородных нейронных структур
- Применение алгоритма перебора деревьев и метода имитации отжига для схемно-структурной оптимизации тепловых сетей
Назад, к списку статей



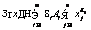 ,
,



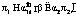 ,
,







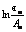
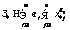 .
.