При компьютерном моделировании поведения систем, которые принято называть сложными, нередко приходится сталкиваться с проявлением феномена скачкообразного, лавинообразного изменения характеристик поведения под воздействием сравнительно плавных изменений одного или нескольких ключевых параметров. Для разрешения подобных проблем целесообразно использовать алгоритмы формирования и роста перколяционных кластеров.
На феномен перколяции впервые обратили внимание Флори [1] и Стокмайер [2] при изучении эффектов формирования гелей и полимеризации. Однако термины «перколяция» и «теория перколяции» в своем современном толковании чаще всего связывают с публикацией работы Броадбента и Хаммерсли [3]. Сегодня теорию перколяции пытаются применять при исследованиях нетривиального поведения самых разнообразных неупорядоченных систем (структур и свойств пористых материалов, прыжковой проводимости в полупроводниках, процессов самоорганизации в образовании фрактальных структур и т.д.).
Заслуживают внимания возможности использования подобного феномена при моделировании процессов распространения массовых эпидемий, когда незначительные изменения вероятности инфицирования отдельных представителей (или группы представителей) могут привести к скачкообразному изменению поведения всей популяции (болезнь из локальной и неопасной переходит в стадию широкомасштабной пандемии).
Для реализации алгоритмов перколяции в качестве наиболее распространенной среды интерпретации принято использовать так называемые решеточные модели. На решетках феномен перколяции отображается цепочками связанных объектов (кластерами), которые в дальнейшем можно распределять по размерам. Если цепочка соединяет две противоположные стороны решетки, то такой кластер и будет перколяционным, сигнализирующим об изменении характера поведения.
Процессы на виртуальных решетках изучены достаточно хорошо, по отношению к ним доказан ряд строгих утверждений. Широкомасштабные приложения подобных процессов зачастую требуют использования возможностей современного метакомпьютинга и разработки соответствующих мультиагентных моделей компьютерной имитации, а также специализированных алгоритмов распараллеливания.
 Так, однопроходный алгоритм многократной маркировки кластера (ММК), предложенный Хошеном и Копельманом [4, 5], позволяет выделять связные подграфы (кластеры) некоторого случайного графа. Всем занятым узлам перколяционной решетки приписываются различные кластерные метки, и всего лишь за один проход удается выяснить, к какому кластеру относится тот или иной узел решетки. Действительно, если узлы решетки нумеруются (номер узла – начальное значение его метки), при последовательном обходе для каждого узла рассматриваются связанные с ним соседи. Каждой такой группе (текущий узел и соседи) ставится в соответствие метка с минимальным номером. Таким образом, на каждом шаге работы алгоритма ММК все замены номеров меток отражаются во всех узлах решетки (то есть, если на некотором шаге метка одного узла заменяется, то заменяются и все остальные метки узлов, равные данной). В итоге все узлы с одинаковыми метками оказываются принадлежащими одному и тому же графу, то есть узлы решетки подразделяются в соответствии с их принадлежностью к тому или иному кластеру.
Так, однопроходный алгоритм многократной маркировки кластера (ММК), предложенный Хошеном и Копельманом [4, 5], позволяет выделять связные подграфы (кластеры) некоторого случайного графа. Всем занятым узлам перколяционной решетки приписываются различные кластерные метки, и всего лишь за один проход удается выяснить, к какому кластеру относится тот или иной узел решетки. Действительно, если узлы решетки нумеруются (номер узла – начальное значение его метки), при последовательном обходе для каждого узла рассматриваются связанные с ним соседи. Каждой такой группе (текущий узел и соседи) ставится в соответствие метка с минимальным номером. Таким образом, на каждом шаге работы алгоритма ММК все замены номеров меток отражаются во всех узлах решетки (то есть, если на некотором шаге метка одного узла заменяется, то заменяются и все остальные метки узлов, равные данной). В итоге все узлы с одинаковыми метками оказываются принадлежащими одному и тому же графу, то есть узлы решетки подразделяются в соответствии с их принадлежностью к тому или иному кластеру.
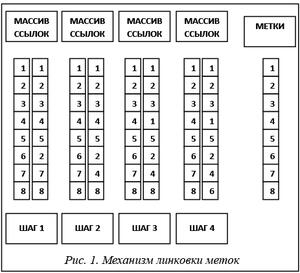
Механизм линковки меток алгоритма ММК Хошена–Копельмана
На суперкомпьютерах с большим количеством процессоров использовался один из многопроцессорных вариантов алгоритма ММК, когда каждому процессору назначалась своя группа узлов. Был выбран многопроцессорный вариант алгоритма, совпадающий с однопроцессорным прототипом за одним исключением: вместо прохода по всей решетке каждый процессор активизировал действия алгоритма ММК только на назначенной ему группе узлов с последующим обменом информацией между процессорами. Алгоритм завершал свою работу, когда на очередном шаге обмена метки всех групп узлов уже не изменялись.
К сожалению, время работы подобного варианта зависит от размера решетки N как O(N2), что для ресурсоемких приложений может оказаться критичным. Алгоритм был усовершенствован механизмом линковки меток, в результате чего удалось добиться зависимости времени его работы от размера решетки N как O(N).
Линковка меток начиналась с того, что пронумерованным узлам решетки ставились в соответствие массив меток и массив ссылок (массив адресов). Значения массива меток и массива ссылок инициализируются номерами соответствующих узлов. Например, для определения метки узла под номером 7 (см. рис. 1) в массиве ссылок следует обратиться к элементу 7. Таким образом, в качестве значения ссылки на элемент 7 берется значение 7. Но если значение ссылки в массиве ссылок оказывается равным номеру элемента этого массива, то по ссылке не надо никуда переходить и остается лишь обратиться к тому же самому номеру элемента в массиве меток (то есть при обращении к элементу 7 массива ссылок получается метка узла под номером 7).
Как видно из рисунка 1, в процессе изменения значений меток изменяются не сами значения меток, а значения элементов массива ссылок. Например, если узел 2 связан с узлом 6 (см. шаг 2), для 6 в массиве ссылок проставляется адрес метки на узел 2. Далее, если узел 1 связан с узлом 4, для 4 в массиве ссылок проставлялся адрес метки на узел 1 (см. шаг 3). Аналогично, если узел 8 связан с узлом 6, для 8 в массиве ссылок проставляется адрес метки на узел 6. После выполнения этих операций для получения значения метки узла 8 необходимо провести описанные выше действия, то есть обращаться к массиву ссылок по номеру 8 и получать адрес 6, обращаться к массиву ссылок по номеру 6 и получать адрес 2, обращаться к массиву ссылок по номеру 2 и получать адрес 2. Так как адрес совпадает с номером узла, следует обращаться в массив меток к элементу под номе- ром 2 и получать для узла 8 метку, равную 2. После подобной перелинковки массив ссылок приводится к виду, когда количество переходов по адресам не превышает 1.
Сбор информации о численности населения
Авторское представление о численности населения формировалось в результате распознавания и анализа карты плотности населения Google Maps http://maps.google.com/?q=http://googis.info/load/0-0-0-688-20. Нанеся на карту плотности решетку с шагом dx=dy в пикселях (см. рис. 2), все ячейки решетки последовательно сканировались и для каждой ячейки определялись ее географические координаты (θ, φ) в соответствии с координатами карты (x, y). После определения координат узлов вычислялась площадь ячейки S в км2.
Так как на карте ячейка имеет форму квадрата, а на поверхности земли форму правильной пирамиды, карта рассматривалась как равноугольная цилиндрическая проекция Меркатора.
Преобразование (θ, φ)®(x, y) раскрывалось как x=c(θ–θ0) и y=c(ath(sin(φ))–ε×ath(ε×sin(φ))), где ε – эксцентриситет земного эллипсоида (он равен 0,08182); θ0 и с – параметры масштаба карты.
 К сожалению, обратное преобразование не выражается в элементарных функциях, в результате чего уравнения y=c(ath(w)–ε×ath(w)), w=sin(φ), w=[–1, 1] приходилось решать численно.
К сожалению, обратное преобразование не выражается в элементарных функциях, в результате чего уравнения y=c(ath(w)–ε×ath(w)), w=sin(φ), w=[–1, 1] приходилось решать численно.
Расстояние R21 между двумя точками с координатами (θ1, φ1) и (θ2, φ2) вычислялось по формулам R21=111×(p12+p22)1/2, p1=(θ2–θ1)×cos((φ2+ +φ1)/2) и p2=φ2–φ1.
Из-за малости ячейки считалось, что она имеет форму прямоугольника. Умножение dx на dy формировало число пикселей в ячейке Npicsels и площадь одного пикселя Sp=S/Npicsels. Таким образом, численность населения N определялась суммированием по всем пикселям.
Для каждого пикселя ставилось в соответствие количество населения Pi=Q×Sp, где Q – плотность, определяемая сопоставлением ее с цветом пикселя в таблице Population Density.
Представление о численности населения формировалось на основе допущения, что наибольшая плотность сосредоточена в городах и его окрестностях, то есть, если численность N>10 000 человек, ячейке соответствовал город с населением N, если 1 000
Если в соседних ячейках располагались города с численностью N>100 000, они объединялись в один большой город. Численность населения всех городов и их координаты заносились в БД.
Формирование перколяционной решетки взаимодействий
Для уменьшения ресурсоемкости задачи представители населения распределялись по кластерам размера n в предположении, что в любом региональном образовании люди одного кластера общаются чаще или реже с людьми из другого кластера.
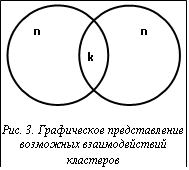 Так, кластеры, взаимодействие которых отображено на рисунке 3, характеризуются 1/k – степенью перекрытия, то есть долей представителей, контактирующих с представителями другого кластера; s – вероятностью контакта за время t между представителями кластеров; n – числом представителей.
Так, кластеры, взаимодействие которых отображено на рисунке 3, характеризуются 1/k – степенью перекрытия, то есть долей представителей, контактирующих с представителями другого кластера; s – вероятностью контакта за время t между представителями кластеров; n – числом представителей.
Пусть p – вероятность того, что после одного контакта один заболевший представитель заразит другого, а pk – вероятность того, что заболевший из одного кластера заразит представителя другого. Тогда число представителей (людей) одного кластера, знакомых с людьми из другого кластера, будет n/k, а число контактов этих людей за время t с людьми из другого кластера – s×n/k. Связь между p и pk начинает выражаться соотношением pk=p×s×n/k.
Для данного n и s=sm=1 месяц pk=p, то есть вероятность одного человека заразить другого равна вероятности представителей одного кластера заразить представителей другого за время sm=1 месяц. Таким образом, sm×n/k=1.
Пусть k=102, то есть каждый сотый из одного кластера имеет знакомого из другого кластера. Установим значение sm, предположив, что представитель одного кластера за 1 год обязательно встретится со своим знакомым из другого, то есть sm=10-1. Тогда n=k/s=103 и в случае t, отличном от tm=1 месяц, pk=p×t/tm.
 Предположим, что кластеризация города имеет сугубо территориальный характер. Тогда соответствующие кластеры города (см. рис. 4) можно объединять в плоскую решетку (для простоты примем, что ячейка решетки квадратная). Введем параметр g0 (концентрация связей) как вероятность того, что кластер имеет связь в пределах одного города с другим кластером, находящимся по соседству.
Предположим, что кластеризация города имеет сугубо территориальный характер. Тогда соответствующие кластеры города (см. рис. 4) можно объединять в плоскую решетку (для простоты примем, что ячейка решетки квадратная). Введем параметр g0 (концентрация связей) как вероятность того, что кластер имеет связь в пределах одного города с другим кластером, находящимся по соседству.
Предположим также, что существует радиус R80, на расстоянии которого находится 80 % всех знакомых из данного города. Если за qij примем количество связей (знакомств) между людьми из города i с людьми из города j, то значение qij можно также воспринимать как характеристику числа знакомств между представителями кластеров двух городов, находящихся на расстоянии, меньшем R80.
Примем за Ni население города i, тогда Mi=Ni/n – это число кластеров одного города. Введем параметры g1, g2 и g3 в качестве межгородских примесных связей (g1 – вероятность того, что кластер данного города имеет связь с кластером города, находящимся на расстоянии 1 0007 000 км). При этом в качестве акцептора связи предпочтение будем отдавать кластерам, находящимся в крупных городах. Оценим f(Mi) и u(Mi, Mj) при R80=f(Mi) и qij=u(Mi, Mj).
При R=k×lgM для г. Москвы с M=104 рассмотрим ситуацию, когда R80=1 000 км. Если k=250, то R=250×lgM. Если с=2, то qij=min(Mi, Mj)/2 и вектор (g0, g1, g2, g3)=(10-1, 10-2, 5×10-3, 10-3).
Располагая правдоподобными данными социологических исследований, параметры модели можно задать более точно.
Моделирование процессов инфицирования
Перед моделированием процессов инфицирования исходная решетка формировалась под воздействием значений следующих параметров: sm – вероятность контакта людей из соседних кластеров за один месяц tm.; 1/k – степень перекрытия кластеров; n – размер кластера; (g0, g1, g2, g3) – набор примесных связей; R80=f(Mi) – радиус, на расстоянии которого находится 80 % всех знакомых из данного города; qij=u(Mi,Mj) – количество связей между кластерами двух городов; набор городов (их население и координаты).
Запуск процесса моделирования распространения эпидемии на анализируемой решетке осуществлялся после задания времени t, за которое инфекция начинала проявлять свою способность распространяться (латентный период); p – вероятности того, что после одного контакта один заболевший заразит представителей всего кластера; указание набора очагов заражения.
Анализируемая решетка отличалась от исходной тем, что в ней каждая связь между узлами имела право на существование с вероятностью pk=p×t/tm.
Применяя многопроцессорный вариант алгоритма ММК анализируемой решетки, вычислялся максимальный размер кластера. Если он оказывался сравнимым с размером анализируемой решетки (отношение количества узлов кластера к количеству узлов анализируемой решетки больше 0,5), кластер воспринимался как соединяющий, то есть фиксировался феномен перколяции. Болезнь, вспыхнувшая в любом узле, с большей степенью вероятности приобретала способность перейти в эпидемию и охватить большую часть перколяционной решетки.
При сборе информации о численности были получены данные по 56 976 городам (общая численность населения которых составляет 6 114 628 510 человек) и сохранены в формате «номер города, численность населения, широта, долгота».
Алгоритм формирования решетки взаимодействия представителей популяции, реализованный на Java, позволил создать исходную решетку и сохранить ее в трех файлах: исходной решетке grid (размером в 475 Мб) и 2 файлах (edges1 и edges2) ребер (общим размером в 429 Мб).
На базе исходной решетки для каждого значения входного параметра p (вероятность заражения при контакте с больным) формировалась (но уже в оперативной памяти) анализируемая решетка и запускался многопроцессорный вариант алгоритма ММК.
Вычисления проводились в Межведомственном суперкомпьютерном центре (г. Москва) на суперкомпьютере mvs100k с общим количеством процессоров 11 680. Так, имитационный эксперимент со значениями входного параметра p от 0,01 до 1 и шагом в 0,01 (при значениях t=3 дня, t=5 дней, t=20 дней и t=30 дней) на 56 процессорах занял 108 минут процессорного времени.
Визуализация полученных результатов проводилась с помощью Google Maps Api (реализация на Java). Выбирался город (как очаг заражения), задавалось количество зараженных узлов в нем, для данных p и t загружался вычисленный ранее массив кластерных меток. Определялись метки зараженных узлов данного города. Производился последовательный обход меток всех узлов из загруженного массива, и, если метка являлась потенциально зараженной, город, в который входил узел с данной меткой, также объявлялся потенциально зараженным. Таким образом, формировался список потенциально зараженных городов. Этот список сохранялся в виде javascript-команд Google Maps API в html-файле. В зависимости от численности населения зараженный город помечался красным кругом определенного размера. Для просмотра результатов html-файл запускался в браузере.
В теории перколяции получен ряд строгих математических результатов, однако основной прогресс достигнут на пути использования компьютерных методов. Работа по разработке новых эффективных алгоритмов постоянно продолжается. Особый интерес представляют алгоритмы для подструктур перколяционного кластера и ал- горитмы, основанные на параллельных вычис- лениях. В данной работе описан параллельный алгоритм многократной маркировки кластеров, который позволяет проводить имитационные эксперименты на многопроцессорных вычислительных системах.
Предложенная мультиагентная модель распространения эпидемий на основе теории перколяции является существенно новым подходом как в имитационном моделировании, так и в направлении моделирования процессов распространения заболеваний. Перколяционный подход позволяет получить кластер, включающий в себя все возможные пути распространения болезни.
Литература
1. Flory P.J.J. Molecular Size Distribution in Three Dimensional Polymers. I. Gelation // Journal of the American Chemical Society. 1941. Vol. 63, № 11, pp. 3083–3090.
2. Stockmayer W.H. Theory of molecular size distribution and gel formation in branched polymers // The Journal of Chemical Physics. 1943. Vol. 11, № 45, p. 11.
3. Broadbent S.K., Hammersley J.M. Percolation Process in Crystals and Mazes // Proc. Camb. Phil. Soc. 1957. Vol. 53, № 3, pp. 629–641.
4. Тарасевич Ю.Ю. Перколяция: теория, приложения, алгоритмы: учеб. пособие. М.: УРСС, 2002. 64 c.
5. Гулд Х., Тобочник Я. Компьютерное моделирование в физике. М.: Мир, 1990. Т. 2. 400 с.





 Так, кластеры, взаимодействие которых отображено на рисунке 3, характеризуются 1/k – степенью перекрытия, то есть долей представителей, контактирующих с представителями другого кластера; s – вероятностью контакта за время t между представителями кластеров; n – числом представителей.
Так, кластеры, взаимодействие которых отображено на рисунке 3, характеризуются 1/k – степенью перекрытия, то есть долей представителей, контактирующих с представителями другого кластера; s – вероятностью контакта за время t между представителями кластеров; n – числом представителей. Предположим, что кластеризация города имеет сугубо территориальный характер. Тогда соответствующие кластеры города (см. рис. 4) можно объединять в плоскую решетку (для простоты примем, что ячейка решетки квадратная). Введем параметр g0 (концентрация связей) как вероятность того, что кластер имеет связь в пределах одного города с другим кластером, находящимся по соседству.
Предположим, что кластеризация города имеет сугубо территориальный характер. Тогда соответствующие кластеры города (см. рис. 4) можно объединять в плоскую решетку (для простоты примем, что ячейка решетки квадратная). Введем параметр g0 (концентрация связей) как вероятность того, что кластер имеет связь в пределах одного города с другим кластером, находящимся по соседству.