Journal influence
Bookmark
Next issue
Neural-fuzzy method for reducing the sensitivity of inverse problems to the variation data
The article was published in issue no. № 4, 2011 [ pp. 72 – 75 ]Abstract:A procedure for the solution of ill-posed problems by using a Kalman filter. Approach to the use of neuro-fuzzy algorithms for reducing the sensitivity of the Kalman filter model for solving inverse problems is proposed.
Аннотация:Рассмотрена процедура решения некорректных задач с использованием фильтра Калмана. Предложен подход к применению нейро-нечетких алгоритмов для снижения чувствительности модели фильтра Калмана при решении об-ратных задач.
| Authors: (midli@mail.ru) - , Ph.D, A.Yu. Puchkov (putchkov63@mail.ru) - Smolensk Branch of the Moscow Power Engineering Institute (Associate Professor), Smolensk, Russia, Ph.D, (putchkov63@mail.ru) - , Russia | |
| Keywords: fuzzy logic, neural network, Kalman filter, inverse problems |
|
| Page views: 11802 |
Print version Full issue in PDF (5.83Mb) Download the cover in PDF (1.28Мб) |
Исследователей в различных областях науки и техники давно интересует решение некорректных задач, к которым относятся и так называемые обратные задачи, когда значения параметров модели должны быть получены из наблюдаемых данных. Из трех условий корректно поставленной задачи – существование решения, его единственность, а также устойчивость по отношению к малым вариациям данных задачи – в обратных задачах наиболее часто нарушается последнее [1]. Так как в отличие от прямых задач обратные могут не соответствовать реальным событиям (нельзя обратить ход процесса, а тем более изменить течение времени), постановки обратной задачи часто являются физически некорректными. При математической формализации физическая некорректность проявляется уже в неустойчивости решения. Таким образом, обратные задачи представляют собой типичный пример некорректно поставленных задач. Для решения некорректных задач, как правило, берутся упрощенные модели объекта или явления, характеризующиеся небольшим числом параметров. Понятно, что на этом пути можно получить лишь приближенные представления о свойствах объекта или характеристиках определяемых величин. Данный подход к решению задачи не использует всех возможностей, предоставляемых современным уровнем точности наблюдений и развитием вычислительной техники. Эти возможности могут найти применение при изучении новых постановок обратных задач и создании устойчивых алгоритмов их решения. К таким алгоритмам можно отнести решения, базирующиеся на методах искусственного интеллекта, в частности, на аппарате искусственных нейронных сетей, широко применяемых в различных прикладных областях [2]. Многообразие типов обратных задач обусловило создание соответствующих методов решения, учитывающих специфику их постановки. Вариантом решения этих задач может быть применение искусственных нейронных сетей с одновременным использованием нечетко-логических методов оценки состояния системы. Основная идея предлагаемого подхода, позволяющего снизить чувствительность решения обратной задачи к вариациям исходных данных, базируется на предварительном применении алгоритма оценивания состояния исследуемой системы, а именно нечеткого фильтра Калмана. Проиллюстрировать подход можно следующей аналогией. Человеческий мозг как биологическая нейронная сеть ежеминутно решает некорректные и обратные задачи, то есть, несмотря на неединственность и неустойчивость решения, восстанавливает по нескольким точкам наблюдаемый объект и все, что его окружает. Делает он это эффективно и быстро, так как использует богатый опыт (априорную информацию). Последовательное применение методов статистики с учетом априорной информации, реально доступной исследователю, позволяет получать устойчивые и эффективные решения обратных задач [3]. Фильтр Калмана как раз позволяет использовать часть априорной информации и, в свою очередь, снизить неопределенность данных для решения обратной задачи нейронной сетью. Применение фильтра Калмана для оценки состояния сталкивается с проблемой получения модели исследуемого объекта, которую называют формирующим фильтром. Эту модель не всегда можно получить на основе применения физических законов, связывающих исследуемые параметры. Например, для экономических объектов такой подход не срабатывает, так как отличительной особенностью источников информации о них является субъективность, а в ряде случаев и противоречивость данных. В этих условиях для решения указанной проблемы вполне уместно использовать методы искусственного интеллекта, а именно методы нечеткой логики, которые позволяют успешно преодолевать отмеченные особенности исходной информации. Структура предлагаемого к решению обратных задач подхода показана на рисунке 1. Ответ гибридной нейронной сети GNN, обозначенный S(t), выступает в качестве решения обратной задачи – нахождения V(t) по x(t). Однако в данном случае на вход сети поступает не зашумленный сигнал u(t)=Cx(t)+N(t), где С – матрица измерений, а оценка Правила нечеткого вывода, лежащие в основе GNN, могут корректироваться экспертами, тем самым предоставляя возможность учета дополнительной информации. Эта возможность отражена блоком BCR. Пунктирными линиями на рисунке обозначены сигналы, участвующие в процессе обучения GNN. В рассматриваемом подходе решение прямой задачи представлено вектором состояния X(t)= =(x1(t), x2(t), …, xn(t)). Предполагается, что переменные состояния xi(t) можно описать системой дифференциальных уравнений: dx1(t) /dt=a11x1(t)+a12x2(t)+…+a1nxn(t), dx2(t)/dt=a21x1(t)+a22x2(t)+…+a2nxn(t), (1) ……………………………. dxn(t)/dt=an1x1(t)+an2x2(t)+…+an n xn(t), где aij – коэффициенты, в общем случае зависящие от времени; dxi/dt – скорости изменения переменных состояния, i=1, …, n. В векторно-матричной форме (1) запишем как
где матрица А имеет вид
Для определения aij используется процедура нечеткого вывода, в основе которой лежит база знаний, содержащая продукционные правила вида П11: ЕСЛИ r1 ЕСТЬ D11 И r2 ЕСТЬ D21 И ... rn ЕСТЬ Dn1, ТО a11 ЕСТЬ A11, П12: ЕСЛИ r1 ЕСТЬ D12 И r2 ЕСТЬ D21 И ... rn ЕСТЬ Dn1, ТО a11 ЕСТЬ A12, …………………………………….. П1m: ЕСЛИ r1 ЕСТЬ D1m И r2 ЕСТЬ D21 И ... rn ЕСТЬ Dn1, ТО a11 ЕСТЬ A1m ,
… где Dij – обозначение j-го (j=1, ..., m) терм-множества значений i-й (i=1, ..., n) нечеткой переменной ri, отражающей i-й фактор, от совокупности которых формируются значения aij; n – количество факторов r; m – количество термов нечеткой переменной ri , i=1, ..., n. Здесь предполагается, что каждый фактор ri имеет одинаковое количество терм-множеств Суждения о параметрах модели объекта эксперты дают на основе статистических данных, представленных с какой-либо временной дискретностью, но, несмотря на это, человеку удобнее и интуитивно понятнее отражать процессы в непрерывном времени. Поэтому можно считать, что полученное описание формирующего фильтра представлено в непрерывном времени. В свою очередь, решение обратной задачи с помощью нейронной сети осуществляется для дискретных моментов времени Δt, поэтому удобнее применять дискретный алгоритм фильтра Калмана, согласуя интервал дискретизации по времени с Δt. Описание дискретного формирующего фильтра сходно с описанием непрерывного, но вид матрицы системы А в этом случае зависел бы от величины Δt, что усложнило бы базу правил ввиду необходимости учитывать в них еще и Δt. Поэтому для получения описания формирующего фильтра в дискретном времени и применения соответствующего алгоритма фильтра Калмана проще провести переход от непрерывного времени к дискретному с помощью предельного перехода Дальнейший расчет дискретного фильтра Калмана осуществляется по следующей методике [4]. 1. В начале такта вычисления 2. Вычисляется априорная матрица ошибок:
где Q(k) – матрица интенсивностей процесса V(k); М[·] – символ математического ожидания; 3. Вычисляется оптимальная матрица усиления фильтра Калмана: 4. На следующем такте понадобится значение апостериорной матрицы ошибок оценивания 5. В конце такта
6. В следующем такте Для реализации данной процедуры задаются начальные условия (априорные значения):
Очередным этапом предлагаемого подхода является выбор типа нейронной сети, которая будет обучаться на выборке {xw, Vw}, где w – количество обучающих наборов. С учетом специфики задачи предложено использовать нейронные сети Элмана, которые относятся к классу рекуррентных нейронных сетей [5]. Важной особенностью архитектуры рекуррентных сетей является наличие блоков динамической задержки и обратных связей, что позволяет таким сетям обрабатывать динамические модели. Сети Элмана состоят их двух слоев – выходного и входного, при этом входной слой охвачен динамической обратной связью с использованием линии задержки. Такая связь позволяет учесть предысторию наблюдаемых процессов и накопить информацию для выработки правильной стратегии управления. Для иллюстрации рассматриваемого подхода была использована среда MatLAB, обладающая широким спектром функций для создания и применения нейронных сетей разных типов, а именно пакет Neural Network. Численный эксперимент проводился с использованием встроенного типа обобщенной регрессионной сети Elman backprop. Алгоритм эксперимента состоит в следующем. 1. Подготовка выборок для обучения сети. Для этого в соответствии с (1) рассчитываются векторы состояний при заданной матрице эволюции системы и подаче на вход гармонического сигнала. Матрица эволюции взята размером 2´2, поэтому векторы состояний имеют по две компоненты – х1 и х2. В результате реализации этого этапа сформируются выборки для обучения нейронной сети, на вход которой будут подаваться векторы состояний, а на выходе получаться значения входного сигнала. Данная процедура отражает процесс решения обратной задачи нахождения причин, которые перевели систему в данное состояние. Будут сформированы две обучающие выборки: train1.dat – для нейронной сети, имеющей один вход (х1) и один выход; train2.dat – для нейронной сети, имеющей два входа (х1 и х2) и один выход. 2. Создание и обучение нейронных сетей nn1 и nn2. Имитируя возможность измерения только одной компоненты вектора состояния, обучение nn1 будет проводиться только по одной компоненте х1 на основе данных train1.dat, а сети nn2 – по двум компонентам – х1 и х2 – на основе данных train2.dat. 3. Наложение шума измерений N(k) и входного случайного процесса V(k) на значения выборки train1.dat и получение тестирующей выборки testing1.dat. 4. Тестирование сети. На вход сети nn1 зашумленная выборка testing1.dat подается непосредственно, а на вход сети nn2 после предварительной обработки фильтром Калмана в соответствии с пунктами 1–6. В результате получаются оценки для компоненты х1 с меньшей (по сравнению с данными из testing1.dat) дисперсией, а также компоненты х2, явно не измеряемой, что позволяет применить сеть nn2 с двумя входами.
Визуальное сравнение этих кривых показывает, что сеть с применением фильтра Калмана значительно лучше справляется с задачей нахождения u(k). Среднеквадратичная ошибка σ определения u(k) за анализируемый промежуток для сети nn2 составила σ2=0,219, а для сети nn1 получено σ1=0,377. Такой запас позволяет сети nn2 находить решение обратной задачи при больших вариациях исходных данных, которые моделируются векторами N(k) и V(k). В частности, для достижения сетью nn2 значения ошибки примерно 0,38 потребовалось увеличение дисперсии входного процесса V(k) с 0,1 до 0,19, то есть почти в два раза большее, чем при проведении эксперимента. Предложенный подход для снижения чувствительности решения обратной задачи к вариациям исходных данных может использоваться при реализации программ и вычислительных алгоритмов в различных прикладных областях, в том числе и экономических, где решения базируются на обработке большого количества статистических данных. Литература 1. Кабанихин С.И. Обратные и некорректные задачи: учебник для вузов. Н.: Сибир. науч. изд-во, 2008. 460 с. 2. Гердова И.В. [и др.]. Новые возможности в решении обратных задач лазерной спектроскопии с применением искусственных нейронных сетей // Изв. РАН: Сер. физ., 2002. № 8. С. 1116–1124. 3. Теребиж В.Ю. Введение в статистическую теорию обратных задач. М.: Физматлит, 2005. 419 с. 4. Изерман Р. Цифровые системы управления. М.: Мир, 1984. 541 с. 5. Круглов В.В., Дли М.И., Голунов Р.Ю. Нечеткая логика и искусственные нейронные сети. М.: Физматлит, 2001. 224 с. |
| Permanent link: http://swsys.ru/index.php?page=article&id=2916&lang=en |
Print version Full issue in PDF (5.83Mb) Download the cover in PDF (1.28Мб) |
| The article was published in issue no. № 4, 2011 [ pp. 72 – 75 ] |
Perhaps, you might be interested in the following articles of similar topics:
- Варианты построения алгоритма поиска решения обратных задач с применением нейронных сетей
- Нечеткий фильтр калмана в структуре алгоритма решения обратных задач для экономических объектов
- Интервально-дифференциальные уравнения в структуре нечеткого фильтра Калмана при управлении сложными технологическими объектами
- Учебная распределенная система управления мобильной колесной платформой с использованием видео- и сенсорной информации
- Интеллектуальная система управления и мониторинга газовой котельной
Back to the list of articles
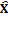 (t) вектора выхода объекта X(t). Применение фильтра Калмана, обозначенного на рисунке FK, позволяет снизить дисперсию входных данных нейронной сети, а следовательно, обеспечить ее работу в менее зашумленном пространстве исходной информации, что, в свою очередь, сказывается на окончательном решении. Блок BFL реализует механизм нечеткого логического вывода, с помощью которого проводится коррекция модели объекта или явления.
(t) вектора выхода объекта X(t). Применение фильтра Калмана, обозначенного на рисунке FK, позволяет снизить дисперсию входных данных нейронной сети, а следовательно, обеспечить ее работу в менее зашумленном пространстве исходной информации, что, в свою очередь, сказывается на окончательном решении. Блок BFL реализует механизм нечеткого логического вывода, с помощью которого проводится коррекция модели объекта или явления.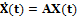 , (2)
, (2)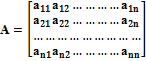 .
. П1m+1: ЕСЛИ r1 ЕСТЬ D11 И r2 ЕСТЬ D22 И ... rn ЕСТЬ Dn1, ТО a11 ЕСТЬ A1m+1,
П1m+1: ЕСЛИ r1 ЕСТЬ D11 И r2 ЕСТЬ D22 И ... rn ЕСТЬ Dn1, ТО a11 ЕСТЬ A1m+1,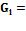
 . Это не является обязательным требованием.
. Это не является обязательным требованием.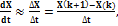 где x(k)=x(kΔt). При выборе Δt учитывают, что оно не должно быть больше времени корреляции исследуемого процесса.
где x(k)=x(kΔt). При выборе Δt учитывают, что оно не должно быть больше времени корреляции исследуемого процесса. происходит расчет оценки:
происходит расчет оценки: 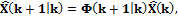 где Ф
где Ф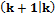 – матрица перехода, подобная матрице А в описании (2).
– матрица перехода, подобная матрице А в описании (2).
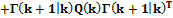 , где
, где  – матрица входа, отражающая влияние процесса V(k), имеющего следующие характеристики:
– матрица входа, отражающая влияние процесса V(k), имеющего следующие характеристики:
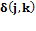 – дельта-функция.
– дельта-функция.
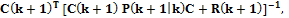 где
где  – матрица интенсивностей шума измерений N(k);
– матрица интенсивностей шума измерений N(k); 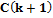 – матрица измерений.
– матрица измерений. . Поэтому после вычисления
. Поэтому после вычисления  находят
находят 
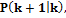 где I – единичная матрица.
где I – единичная матрица.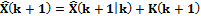
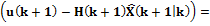
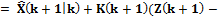
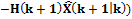 .
.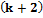 процедура повторяется на основе найденных для
процедура повторяется на основе найденных для 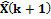 ,
, 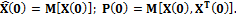
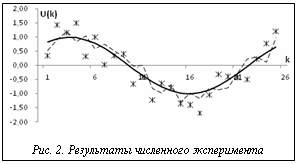 Результаты численного эксперимента показаны на рисунке 2. Сплошной линией на графике изображен истинный сигнал u(k), пунктирной – ответ сети nn2, звездочками – ответ сети nn1.
Результаты численного эксперимента показаны на рисунке 2. Сплошной линией на графике изображен истинный сигнал u(k), пунктирной – ответ сети nn2, звездочками – ответ сети nn1.