Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Алгоритм минимизации скалярной функции многих переменных при интервальных ограничениях на переменные
Аннотация:Рассмотрен поисковый алгоритм минимизации скалярной функции многих переменных при неявном задании функции и интервальных ограничениях на переменные. Суть алгоритма, в предположении, что наименьшее значение функция принимает в одной из вершин гиперпараллелепипеда – области допустимых значений аргументов, состоит в последовательном обходе вершин из начальной точки в сторону убывания функции. Предложена программная реализация алгоритма в среде MATLAB.
Abstract:The article deals with the search scalar function algorithm minimization of many variables with implicit function and interval limitation on variables. The main idea of algorithm, that the least value the function takes at one of the hypeparallelepiped apexes – the area of possible values argument, is in successive bypass of apexes from the initial point to the function decrease. The program algorithm realization is suggested in the MATLAB sphere.
| Авторы: Бояринов Ю.Г. (byg@yandex.ru) - Филиал Московского энергетического института (технического университета) в г. Смоленске, кандидат технических наук, Дли М.И. (midli@mail.ru) - Филиал Московского энергетического института (технического университета) в г. Смоленске (профессор, зам. директора по научной работе), г. Смоленск, Россия, доктор технических наук | |
| Ключевые слова: программная реализация алгоритма, интервальные ограничения на переменные, скалярная функция многих переменных, алгоритм минимизации |
|
| Keywords: program algorithm realization, many variables, scalar function of many variables, minimization algorithm |
|
| Количество просмотров: 10429 |
Версия для печати Выпуск в формате PDF (4.85Мб) |
Задача нахождения наименьшего значения скалярной функции многих аргументов при наличии интервальных ограничений на аргументы на практике является достаточно типовой. Для ее решения разработано множество алгоритмов (см., например, [1–3]), однако, как правило, подобные алгоритмы хорошо работают только при небольшом числе аргументов. Если же это число велико – десятки и сотни, то многие из известных алгоритмов просто неприменимы. Для подобных ситуаций пригодными оказываются только так называемые алгоритмы большой размерности, реализованные, в частности, в системе компьютерной математики MATLAB [4]. Однако использовать возможности этой и других аналогичных систем не всегда целесообразно ввиду их громоздкости, иногда удобнее иметь автономные программы, созданные на языке высокого уровня. В статье рассмотрена разновидность алгоритма большой размерности, отличающаяся простотой программной реализации. Постановка задачи. Предполагается, что в общем случае неявным образом задана скалярная функция x1 min£x1£x1 max, x2 min£x2£x2 max, . . . xi min£xi£xi max, . . . xn min£xn£xn max, или, в векторной форме, где Число переменных может быть значительным, например до сотни. Дополнительно предполагается, что функция Требуется найти точку x*ÎSx, в которой функция f достигает наименьшего значения, то есть, иными словами, решить оптимизационную задачу
Алгоритм решения. Выдвинутое предположение, что искомая функция не имеет экстремумов внутри допустимой области изменения аргументов, позволяет осуществлять поиск точки наименьшего значения функции среди граничных (угловых) точек области Sx. Данная область, в соответствии с ограничениями (1), представляет собой гиперпараллелепипед в n-мерном пространстве аргументов. Суть алгоритма, как отмечалось, в последовательном переборе вершин гиперпараллелепипеда, так, что осуществляется движение к вершине, где значение функции наименьшее. Приведем описание алгоритма. Требуемая входная информация: размерность задачи n (число аргументов функции), подпрограмма вычисления значений функции f(x1, x2,…, xn) при заданном наборе ее аргументов, границы изменения аргументов – векторы Начало. 1. Ввод исходных данных: числа переменных n, предельного числа итераций N, задание подпрограммы вычисления функции Формирование вектора 2. Принятие 3. i=1. 4. Переход к i-й соседней с базовой вершине гиперпараллелепипеда 5. Расчет 6. Сравнение 7. i=i+1. 8. i>n? Если нет (то есть обойдены не все n соседних с текущей базовой точек гиперпараллелепипеда), то переход к п. 4 алгоритма. 9. Вывод информации об Конец. Вариант алгоритма был реализован с помощью «студенческого языка» программирования Турбо Бейсик; без подпрограммы вычисления значения функции основной текст программы имел 40 строк и объем в несколько Кб; компилированный вариант программы, реализующей алгоритм, имел объем всего в 27 Кб. Программа достаточно устойчиво работала на многих модельных примерах при числе переменных n£100. Время счета, естественно, зависело от n и от сложности вычисления значения функции Пример. Пусть задана функция f(x1, x2, …, x6) вида (неявного)
при ограничениях: 1.9£x1£2.1, 0.9£x2£1.1, 0.9£xу£1.1, 2.8£x4£3.2, 1.9£x5£2.1, 1.9£x6£2.1. Требуется в условиях этой задачи найти наименьшее значение функции (и точку, в которой она принимает это значение). Решение. Здесь n=6, ограничение и задание функции соответствуют принятой постановке задачи. В предположении, что точкой минимума является одна из угловых точек области определения (гиперпараллелепипеда), найдем данную точку, используя разработанный алгоритм при начальном приближении Полученный результат: С целью проверки этого результата минимум рассматриваемой функции производился в среде системы компьютерной математики MATLAB с помощью функции fmincon [4] при начальном приближении f=0.4262, ans=1.9000 1.1000 1.1000 2.8000 1.9000 1.9000. Как видно, они совпадают с полученными при помощи предложенного алгоритма, что подтверждает его работоспособность. Разработанный алгоритм и реализующая его программа могут эффективно применяться в составе интегрированного пакета для решения оптимизационных задач с целью поиска минимума скалярной функции большого числа переменных при наличии ограничений на переменные типа нестрогих неравенств. Алгоритм эффективен, если априори известно, что минимизируемая функция не имеет точек экстремума внутри области ограничений и по своему виду близка к линейной. Достоинствами алгоритма являются его простота с вычислительной точки зрения, возможность работать с большим – до сотни и более – числом n аргументов и высокая скорость поиска точки минимума. Сходимость алгоритма 2n всегда гарантируется ввиду конечности точек поиска (вершин гиперпараллелепипеда). Литература 1. Аоки М. Введение в методы оптимизации. М.: Наука, 1977. 2. Банди Б. Методы оптимизации: вводный курс. М.: Радио и связь, 1988. 3. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. М.: Лаборатория Базовых Знаний, 2000. 4. Дьяконов В., Круглов В. Математические пакеты расширения MATLAB: Специальный справочник. СПб: Питер, 2001. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=2374 |
Версия для печати Выпуск в формате PDF (4.85Мб) |
| Статья опубликована в выпуске журнала № 4 за 2009 год. |
Назад, к списку статей



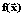 многих вещественных переменных x1, x2,…, xn, или, иначе, векторного аргумента
многих вещественных переменных x1, x2,…, xn, или, иначе, векторного аргумента 
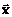 =[x1, x2, …, xn]T (здесь T – символ транспонирования). На переменные наложены интервальные ограничения в форме нестрогих неравенств:
=[x1, x2, …, xn]T (здесь T – символ транспонирования). На переменные наложены интервальные ограничения в форме нестрогих неравенств: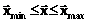 , (1)
, (1)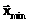 =[x1min, x2min, …, xnmin]T,
=[x1min, x2min, …, xnmin]T, 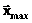 =[x1max, x2max, …, xnmax]T.
=[x1max, x2max, …, xnmax]T.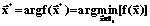 . (2)
. (2)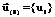 , где i=1, 2 ,…, n; элемент ui равен 1 или -1, при этом, если ui=1, то xi=xi max, если ui= -1, то xi=xi min (вектор
, где i=1, 2 ,…, n; элемент ui равен 1 или -1, при этом, если ui=1, то xi=xi max, если ui= -1, то xi=xi min (вектор 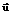 введен для удобства обхода вершин области определения функции, его элементы – индикаторы значений компонент
введен для удобства обхода вершин области определения функции, его элементы – индикаторы значений компонент 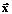 ).
).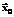 по вектору начального приближения
по вектору начального приближения 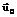 .
.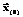 ) за базовую точку вычислений; расчет значения функции
) за базовую точку вычислений; расчет значения функции 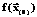 .
.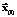 путем замены значения i-го элемента вектора
путем замены значения i-го элемента вектора 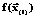 .
.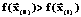 , то
, то  =
=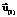 и переход к п. 3 алгоритма.
и переход к п. 3 алгоритма. и
и 
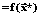 как о достигнутой точке наименьшего значения функции и о значении функции в этой точке соответственно.
как о достигнутой точке наименьшего значения функции и о значении функции в этой точке соответственно. .
. (3)
(3)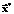 =[1.9 1.1 1.1 2.8 1.9 1.9]T,
=[1.9 1.1 1.1 2.8 1.9 1.9]T, 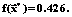
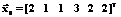 . Результаты вычислений следующие:
. Результаты вычислений следующие: